1 Record Linkage and Data Analysis
Combining data from diverse sources is a critical component of data analysis across computational fields. Linking disease outbreak patients with water supply locations gave John Snow new insights into how cholera spreads (Snow Reference Snow1855), forming the foundation for modern public health; merging Congressmembers’ campaign donation data with their votes cast addresses the influence of money in politics (Wawro Reference Wawro2001); and combining student records from multiple schools enables researchers to assess the effects of educational policies many years down the line (Alicandro et al. Reference Alicandro, Frova, Sebastiani, Boffetta and Vecchia2018).
In the best-case scenario, both datasets share in common several unique identifying columns with identical formatting that unambiguously connect observations across sources. All common data analysis software includes tools to perform this data merge. However, the best-case scenario rarely appears in practice. More commonly, the two datasets contain different and incomplete sets of identifiers, with different formatting. The first dataset might contain a single variable indicating an individual’s name, whereas the second dataset might have columns for first name, middle name, last name, and suffix; the first dataset might indicate organizations by their full names, whereas the second dataset might only include abbreviations. A correct match identifies that Jenny Smith and Jennifer A. Smith are the same person, or that “JP Morgan,” “jpm and associates,” and “JPM” are all the same company as “J.P. Morgan Chase and Co.”
In both cases, there are two datasets each with rows representing entities: a person in the first example, and an organization in the second. When there are multiple variables to identify which entities appear in both datasets—name, age, and date of birth, for example—it is called a record linkage problem (Fellegi and Sunter Reference Fellegi and Sunter1969; Jaro Reference Jaro1989; Larsen and Rubin Reference Larsen and Rubin2001). A large and growing literature reflects the importance of this problem, applying probabilistic and Bayesian methodologies to compute match confidences (Christen Reference Christen2005; Enamorado, Fifield, and Imai Reference Enamorado, Fifield and Imai2019; McVeigh, Spahn, and Murray Reference McVeigh, Spahn and Murray2020), increasing both the precision (the proportion of identified matches that link the same entities) and recall (the proportion of correct matches found to total matches that exist).
Since this merging step is preliminary to almost all applied data analysis, finding correct matches, and many of them, is greatly consequential. Too few matches and subsequent analyses will have insufficient statistical power; if too many matches are incorrect, or if they are systematically incorrect in an important way, any following results may be severely biased. This induces a methodological trade-off: researchers may choose to retain fewer matches of higher quality and bear the consequences of reduced observations, or accept a less stringent standard of match certainty and risk compromising their results.
1.1 Fuzzy String Matching
This paper offers improvements on this precision-recall trade-off for an important edge case of (and component of) the record linkage problem. When the two datasets share only a single imperfect identifier, this is sometimes called the fuzzy string matching problem (Filipov and Varbanov Reference Filipov and Varbanov2019; Hall and Dowling Reference Hall and Dowling1980). Without leveraging similarities across multiple identifying columns, researchers faced with fuzzy string matching problems have less information and fewer tools at their disposal. Those that exist fall into three categories. The most common solutions involve one or more variants of edit distance (Ristad and Yianilos Reference Ristad and Yianilos1998). Levenshtein distance, for example, calculates the minimum number of insertions, deletions, or replacements needed to convert one string to another: “JP Morgxn” converts to “J.P. Morgan” by inserting two periods and replacing the accidental “x” with an “a” for an edit distance of 3. Consequently, Levenshtein distance is very effective for fixing typos, but relatively ineffective at matching “JP Morgan” to “JP Morgan Chase” since that requires six new insertions.
A second category of tools examines substrings: the two most common are longest common substring (LCSTR), which finds the longest substring in common to both strings, and Jaro–Winkler dissimilarity, which examines character index proximity. LCSTR similarity might take the strings “JP Morgxn” and “JP Morgan Chase,” and note that both share the 7-gram “JP Morg.” Jaro–Winkler distance upweights n-gram matches early in the string according to a tuning parameter, and in those ways, they both avoid the pitfall that Levenshtein distance falls into above.Footnote 1 However, they fail where Levenshtein distance does not inasmuch as they are sensitive to typos, since both may miss “PJ Mrogan Chsae” as a misspelled match for “JP Morgan Chase.”
A final set, composition-based measures, includes Jaccard similarity and cosine similarity. Jaccard similarity is the ratio of in-common characters to total characters. By representing a string as a bag-of-letters, cosine similarity creates a letter frequency vector for each of two strings and calculates the cosine of the angle between those vectors. Cosine similarity is thereby robust to switched letters, correctly matching “JP Morgan Chase” with “PJ Mrogan Chsae,” but is less successful in matching “JP Morgan” to “JP Morgan Chase” like Levenshtein distance.
While there are dozens of variants of string-distance tools, there is little guidance for how applied researchers can choose among them when different methods invariably produce different sets of matches. But critically, while Levenshtein distance is best at identifying typos and Jaccard similarity is best when typos are rare, most applied problems include both types of errors (Table 1). The optimal tool would intelligently use Levenshtein distance to correct typos, Jaro–Winkler distance to finish incomplete strings, and cosine distance when letters are swapped, as well as any of the dozens of other tools like Sorensen–Dice distance or the Tversky index as appropriate, custom-fitted to the application at hand.
Table 1 Each row indicates a possible matched pair of String 1 and String 2, and contains the true match status and four different string-distance metrics. In the first row, String 1 and String 2 are identical, so all distance scores are 0.

We propose an ensemble learning approach, aggregating these and many more string-distance metrics to collaboratively address the fuzzy string matching problem. Drawing inspiration from Kaufman, King, and Komisarchik (Reference Kaufman, King and Komisarchik2021) as a method for quantifying “knowing it when you see it,” we design and implement a human-in-the-loop (HITL) algorithm called Adaptive Fuzzy String Matching (AFSM) for combining string matching methods into a metalearner. We think of this procedure as a method for generating bespoke string-distance measures tailored to each new application. We find that it optimizes both precision and recall, producing better matched datasets for applied research. We show its increased effectiveness over current best practices through a series of diverse applications, and introduce open-source software to implement our procedures.
2 An Adaptive Algorithm
The key insight to AFSM is leveraging one of the foremost principles of human–computer interaction: have computers do what they do well, and let humans do what they do well (Kaufman et al. Reference Kaufman, King and Komisarchik2021; Lazar, Feng, and Hochheiser Reference Lazar, Feng and Hochheiser2017; Norman and Draper Reference Norman and Draper1986). Drawing inspiration from the literatures on adaptive machine learning and text-as-data (Enamorado Reference Enamorado2018; Miller, Linder, and Mebane Reference Miller, Linder and Mebane2019), we find that although computers can quickly identify large sets of possible matches, only humans can quickly identify whether a proposed match is correct (Mozer et al. Reference Mozer, Miratrix, Kaufman and Anastasopoulos2018).
Leveraging this, we design an algorithm of three steps. First, a computational model proposes matches. Second, an HITL identifies which proposed matches are correct or incorrect. Finally, the computer refines its model and proposes new matches to repeat the cycle. The training labels indicate whether a pair of strings is a match; the feature set consists of a number of string-distance metrics. Note that while this model does require a training set, due to Step 2, we find that one training set suffices for our three applications. For more details on this phenomenon, our implementation of the model, the model’s properties, and its drawbacks,Footnote 2 see the Online Supplement.
We are agnostic as to which supervised learner our algorithm uses; we experiment with a number of options and select a random forest model as our preferred learner, and as such, our procedure is akin to a boosted trees model (Kaufman, Kraft, and Sen Reference Kaufman, Kraft and Sen2019). After initializing the algorithm with a training set and producing a baseline model, we repeat the HITL cycle until the model consistently produces few false positive matches or the model converges.Footnote 3 For small datasets, this number of iterations may be 1 or even none; for bigger problems, it may be as many as 10.
2.1 Algorithm Notation
Consider an HITL process with I iterations, a strings in the first set and b strings in the second set, and X string-distance metrics. Each HITL iteration will examine the n predictions.

3 Applications and Validation
Across three applications, we illustrate different facets and use cases of our method; in each, we show how our method produces matches robust to a wide variety of typos, abbreviations, mispunctuations, and more. The first application matches organizations, the second matches geographies, and the third matches individuals. The first example involves many HITL iterations, the second example just one, and the third example relies only on the baseline model with no additional researcher input. We validate each application with comparisons to human labeling, and more details for each are available in the Online Supplement.
3.1 Matching Campaign Donors to Amicus Cosigners
Our first application is to interest group ideology. We match a dataset of campaign donations to interest groups (Bonica Reference Bonica2014) to a dataset of amicus curiae co-signing organizations (Box-Steffensmeier, Christenson, and Hitt Reference Box-Steffensmeier, Christenson and Hitt2013) in the interest of studying the ideological behavior of amicus curiae (Abi Hassan et al. 2020). To validate that AFSM produces higher precision and recall than alternative methods, we conduct two evaluation studies. The first study addresses recall: we manually identify a number of true matches between the amicus curiae and campaign donation data, and withhold those matches from our training set; we can estimate recall as the proportion of withheld matches that a method identifies (see Figure B.1 in the Online Supplement). The second study addresses precision: we sample 200 proposed matches from each method (4,000 total) and present them to human coders on Amazon.com’s Mechanical Turk. We ask each respondent to examine a proposed match and identify whether that match is correct or incorrect. We triple-code each pair, and estimate precision as the proportion of model-identified matches that the majority of human coders label as correct (Figure 1).
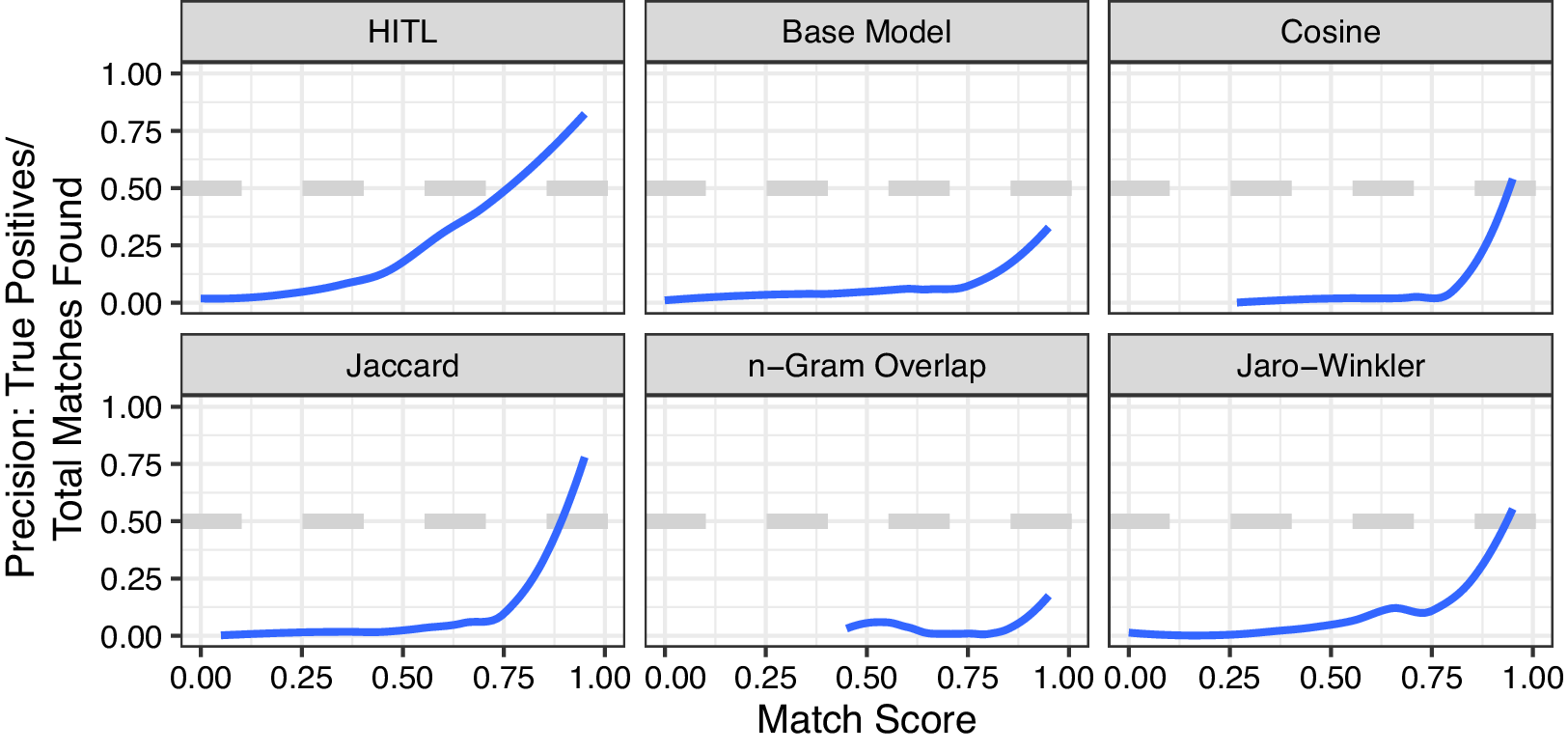
Figure 1 Match precision increases as the predicted match probability increases for the human-in-the-loop (HITL) model, the baseline model, and four constituent measures. At a confidence of 0.95 or greater, the HITL model achieves 88.0% precision.
When the AFSM model identifies a match with confidence between 0.95 and 1, it is correct 88.0% of the time. The next-best performing measure, Jaccard similarity, only achieves 85.0% precision at a match score of 0.95–1, and 53.0% with a score of 0.9–0.95. Jaro–Winkler achieves 76.3% precision in the highest category. We compare Area Under the Receiver Operating Characteristic results for the AFSM model, the baseline model, and Jaccard similarity in the Online Supplement.
3.2 Matching Misspelled Cities in PPP Data
Our second application turns from organizations to geographies. The Paycheck Protection Program (PPP), instituted as a stimulus for US small businesses in 2020, awarded loans of more than $150,000 to more than 600,000 businesses. Its publicly released loan-allocation data include the approximate dollar amount, business name, and location of loan recipients. Importantly, the city name variable is often misspelled. First, removing any cities that are spelled correctly, we compare every remaining city with the cities in list of almost 30,000 cities that are within the same state. AFSM identifies matches among both common and uncommon misspellings: “PHILDADELPHILA” and “PHILLADELPHIA” both match Philadelphia, PA; “BERKLELEY” and “BERKLEY” both match Berkeley, CA; “BKLYN” matches to Brooklyn, NY. We successfully match “N LOS VEGAS” and “NO LOS VEGAS” to the city of North Las Vegas, NV; we correct missing or extra spacing, trailing punctuation, and even uncommon abbreviations like “PLSDS” to “PALISADES.” Above a 0.95 confidence, every identified match is a true match as per a manual coding; above 0.75, most of the incorrect matches involve cardinal direction errors (“N. HOLLYWOOD” matching to “W HOLLYWOOD,” for example). See the Online Supplement for more details.
3.3 Identifying Incumbent Voting
A final application illustrates AFSM’s utility without the HITL step. The 2016 Cooperative Congressional Election Study (Ansolabehere and Schaffner Reference Ansolabehere and Schaffner2017) asked respondents to identify the Congressional candidate for whom they voted in 2016, and later, using geolocation data, identified each respondent’s incumbent Member of Congress. However, since the standardized version of the incumbent names rarely match respondents’ typed candidate name, determining which respondents cast votes for their incumbent is a fuzzy string matching problem. We apply our base model trained on our interest group data and find that it captures nearly all the true positives in the dataset: the first HITL iteration returns no new true-positive matches. For accuracy, we find that with a confidence threshold of 0.2, the base model achieves both true-positive and false-negative rates of less than 1% compared to a manual coding, indicating near-perfect accuracy (see Table B.3 in the Online Supplement).
4 Discussion
This paper introduces a method and associated software for merging datasets with only a single, error-prone common column. By leveraging the complementary advantages of human coders and computer models, this method is robust to a diverse set of string errors and requires no additional training data in applying it to new domains. We show that it productively applies to matching problems relating to people, places, and organizations, and argue that this robustness and broad applicability arises from its adversarial learning process—having an HITL iteratively adds training observations where the model performs poorly.Footnote 4 This tool is broadly useful on its own; researchers may also incorporate its confidence scores as a string-distance measure in performing probabilistic record linkage. We are optimistic that this work will facilitate research across a wide range of disciplines and open up new avenues for analysis, for example, in problems like reconciling the names of disappeared or deceased people in civil conflicts.
Acknowledgments
The authors would like to thank Sahar Abi Hassan, Jan Box-Steffensmeier, Dino Christenson, Shiro Kuriwaki, and Brian Libgober for their help in motivating this project and in providing data, and Ken Benoit, Ted Enamorado, Mayya Komisarchik, Kevin Munger, and three anonymous reviewers for comments and feedback. Special thanks go to Laureano Nisenbaum, Adrian Pearl, and Orion Taylor for their work in helping to develop and implement the tools described herein, and to Le Bao for his work ensuring that the paper meets replicability standards.
Data Availability Statement
Replication data for this article (Kaufman and Klevs Reference Kaufman and Klevs2021) are available at https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/4031UL. An R library implementation of the model in this paper is available at https://github.com/aaronrkaufman/stringmatch.
Supplementary Material
For supplementary material accompanying this paper, please visit http://doi.org/10.1017/pan.2021.38.




