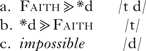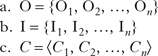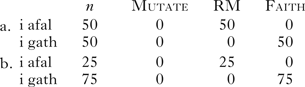1 Introduction
In this paper I show that there are particular frequency effects governing the mapping from input to output. I demonstrate that, while they appear to conflict with each other, a simple unified account is possible. For this demonstration, a generic version of Optimality Theory (McCarthy & Prince Reference McCarthy and Prince1993, Prince & Smolensky Reference Prince and Smolensky2004) is assumed, but the proposal is compatible with any constraint-based theory. I will provide a unified account for three statistical effects: (i) the underrepresentation of marked phonological elements, (ii) the underrepresentation of phonological changes and (iii) the overrepresentation of morphologically conditioned phonology.
The rarity of marked elements is well established. Typologically marked elements tend to be rarer than typologically unmarked elements in languages that have both. This applies both to marked elements and to marked configurations. The underrepresentation of phonological mappings between input and output is established by Hammond (Reference Hammond2013): forms that undergo phonological changes between input and output are underrepresented with respect to forms that do not undergo changes. That there is overrepresentation of forms that undergo phonological changes conditioned by morphology is demonstrated by Hammond (Reference Hammond2014). The latter paper provides the outlines of how this might be treated in the context of the underrepresentation effect. Here I put all these pieces together into an explicit account that also treats the typological effects and test it with a number of additional phenomena not previously treated.
The organisation of this paper is as follows. I begin with classical frequency effects in the domain of typological markedness, reviewing data from English. The general phenomenon is that marked elements are less frequent than unmarked elements. Next, I turn to similar effects in the domain of phonological mapping, again using data from English. I show that phonological changes (qua faithfulness violations) are underrepresented in comparison with non-changes. In §4, I show that consonant mutation in Welsh exhibits the opposite skewing: changes induced by consonant mutation are overrepresented compared with non-changes. I next consider a variety of corpus data from English and Welsh, demonstrating that it is the morphological aspect of consonant mutation that causes this apparent different behaviour, and provide an account of this difference. Finally, I conclude with a review of the general empirical results, the theoretical claim, remaining questions and directions for future research.
2 Typological markedness
In the following, I take typological markedness as an opposition between two elements a and b cross-linguistically. The element a is typologically marked with respect to b just in case a does not occur in a system unless b is there. In other words, the presence of a in a language implies the presence of b: a→b (Hammond et al. Reference Hammond, Moravcsik, Wirth, Hammond, Moravcsik and Wirth1988).
It is well-known that typologically marked elements tend to be less frequent than unmarked elements in the phonological systems that actually contain them.Footnote 1 For example, [d] is more marked typologically than [t] and, in systems that have both, [d] tends to be less frequent.Footnote 2 Marked phonological elements and configurations are avoided in surface/output representations (Jakobson Reference Jakobson1968).
We can see this effect in English with word-initial coronal stops using the Brown corpus (Kučera & Francis Reference Kučera and Francis1967).Footnote 3 Voiced stops are more marked than voiceless stops typologically. This is evidenced by the number of languages that have voiceless stops, but not voiced stops, and the virtual absence of languages with voiced stops, but not voiceless stops. Focusing, for convenience, on word-initial position, what we find is that, in English, voiced stops are observed more rarely than voiceless stops. More specifically, if we assume they should be equally frequent, the occurring distribution is significantly different, as shown in Table I.Footnote 4
Table I Distribution of word-initial [t] and [d] in the Brown and Buckeye corpora. The distribution is significant: Brown χ2(1, N = 79988) = 4752.863, p < 0.001; Buckeye χ2(1, N = 22389) = 326.330, p < 0.001.
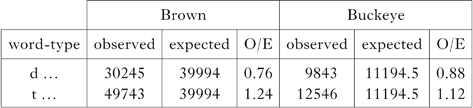
One might doubt a comparison based on a written corpus, but, as also shown in Table I, we find the same effect with the spoken Buckeye corpus (Pitt et al. Reference Pitt, Dilley, Johnson, Kieling, Raymond, Hume and Fosler-Lussier2007), which has 284,732 words.
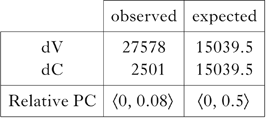
There are similar effects with phonotactic or contextual markedness. For example, consonant clusters are more marked than singletons cross-linguistically; if a language has clusters, it will necessarily have singletons, but not vice versa. Correspondingly, if a language has clusters, they will be less frequent than the corresponding singletons. For example, English word-initial singleton [d] is more frequent than word-initial [dC] clusters in both the Brown and Buckeye corpora, as shown in Table II.
Table II Distribution of word-initial [dV] and [dC] in the Brown and Buckeye corpora. The distribution is significant: Brown χ2(1, N = 30079) = 20906.810, p < 0.001; Buckeye χ2(1, N = 9751) = 8290.235, p < 0.001.

Prince & Smolensky (Reference Prince and Smolensky2004) show that a framework like OT can accommodate systemic markedness, i.e. implicational generalisations of the form: if a language has [d], it will also have [t]. The explanation for this comes from the claims that: (i) there is a universal set of constraints, and (ii) these constraints can interact only via strict ranking. On the assumption that we have a faithfulness constraint Faith and a markedness constraint *d, it follows that only the two kinds of phonological system in (1a, b) are possible.
-
(1)

One ranking gives us (1a), the other gives us (1b), but there is no ranking of these two constraints that will produce (1c).
However, orthodox OT provides no direct account of statistical markedness. We turn to this in the following section.
3 Phonological changes
The distributional patterns discussed in the previous section extend to other parts of the phonology. Specifically, the same kinds of skewings apply at the phrasal level and to input–output mappings.
Marked phonological configurations can be repaired phonologically as well. These changes are also statistically avoided. An example is the Rhythm Rule (Liberman & Prince Reference Liberman and Prince1977, Hammond Reference Hammond1984, Hayes Reference Hayes1984).Footnote 5 The Rhythm Rule refers to the phenomenon whereby a primary stress in English is shifted leftward onto a preceding secondary stress if it would otherwise occur too close to a following stress. These two factors, i.e. clash and the presence of a preceding secondary stress, are separated in (2).
-
(2)

In (2a) we see stress shifting leftward because the primaries are too close. In (2c) we see no shift, because there is no preceding secondary to shift the primary to. In (2b) and (2d) we see no shift, as the stresses are not close enough.
Hammond (Reference Hammond2013) demonstrates that cases (a) and (c) are statistically underrepresented, using the tagged Brown corpus and the CMU pronouncing dictionary.Footnote 6 The basic idea is to compare the distribution of these items in environments where the Rhythm Rule applies with those where it doesn't. It's a little complex to do this, because stress isn't marked in the tagged Brown corpus. It's also difficult because the environments where shift occurs depend on whether the relevant item is in a syntactic phrase with the following item and the stress of the first item is close enough to that of the second. Following Hayes (Reference Hayes1984), I assume that stress shift aims for four-syllable intervals; hence two-syllable modifiers will be in the appropriate stress configuration if the following word has a stress on the first or second syllable. This is, of course, always true in English (e.g. Chomsky & Halle Reference Chomsky and Halle1968). The syntactic environment is approximated by comparing prenominal environments to all others. This isn't exact. For example, we might expect adjectives before other adjectives to constitute a Rhythm Rule environment, and our search strategy groups these incorrectly. The idea is that the prenominal examples will be dominated by appropriate syntactic configurations for the Rhythm Rule, and examples of the second non-prenominal sort less so. This certainly isn't perfect, but it avoids having to do a full syntactic parse.
There are 1,161,192 words in Brown and 127,008 words in CMU. There are 64,028 adjective tokens in Brown and 8063 adjective types. Of these, 4049 occur in the CMU dictionary, of which 1281 are disyllabic and can be analysed.Footnote 7 Table III gives just the general pattern. As we might expect, there are a lot more trochaic adjectives than iambic, and a lot more words with a single stress than two stresses, as in Table III.
Table III Distribution of stress in two-syllable adjectives in the Brown corpus. (The adjectives also occur in the CMU dictionary.)
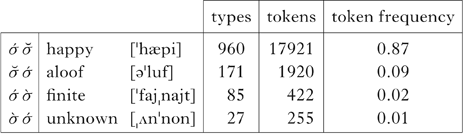
If we break these up into prenominal vs. non-prenominal tokens, we get Table IV.
Table IV Distribution of stress in two-syllable prenominal (vs. elsewhere) adjectives in the Brown corpus. (The adjectives also occur in the CMU dictionary.) The distribution prenominally is significantly different from that non-prenominally (χ2(1, N = 7988) = 270.205, p < 0.001).
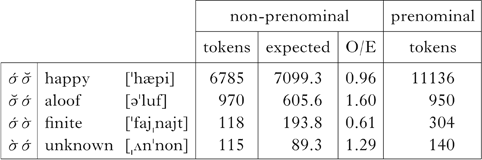
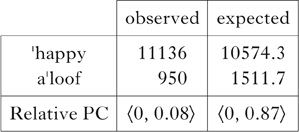
This can be made more precise though. Two distributional patterns are important here. First, the distributions of items like happy and aloof are significantly different with respect to prenominal and non-prenominal environments. In prenominal position, words like aloof represent 8% of adjectives with no secondary stress, while in non-prenominal position they account for 13%. This shows us that unresolvable clash, a marked configuration, is underrepresented, as in Table Va.
Table V Separating the distributions for (a) unresolvable and (b) resolvable stress configurations with prenominal adjectives in the Brown corpus. The differences are significant: (a) χ2(1, N = 7755) = 231.300, p < 0.001; (b) χ2(1, N = 233) = 34.290, p < 0.001.

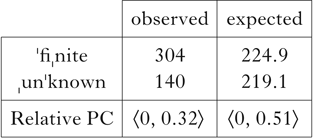
Second, the distributions of items like finite and unknown are significantly different across prenominal and non-prenominal environments as well, as in Table Vb. In prenominal position, words like unknown represent 32% of adjectives with secondary stress, while in non-prenominal position, they account for 49%. This shows that resolvable clash is also underrepresented.
The Buckeye corpus shows the same general pattern. I first tagged the corpus with the Stanford part-of-speech tagger (Toutanova et al. Reference Toutanova, Klein, Manning and Singer2003).Footnote 8 The procedure was then the same as above, and yielded the basic distribution in Table VI.
Table VI Distribution of stress in two-syllable adjectives in the Buckeye corpus.
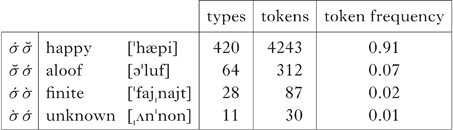
Prenominally vs. elsewhere in the Buckeye corpus, we find a similar distribution to what we saw in the Brown corpus, as in Table VII.
Table VII Distribution of stress in two-syllable prenominal (vs. elsewhere) adjectives in the Buckeye corpus. The distribution prenominally is significantly different from that non-prenominally (χ2(3, N = 2226) = 71.140, p < 0.001).
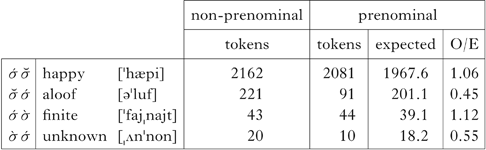
Overall in the Buckeye corpus, the distribution prenominally is significantly different from that non-prenominally, just as in the Brown corpus.
As with the Brown data, two distributional patterns are important here. First, the distributions of items like happy and aloof are significantly different with respect to prenominal and non-prenominal environments. In prenominal position words like aloof represent 4% of adjectives with no secondary stress, while in non-prenominal position they account for 9%. This shows that unresolvable clash, a marked configuration, is also underrepresented in the Buckeye corpus, as in Table VIIIa.
Table VIII Separating the distributions for (a) unresolvable and (b) resolvable stress configurations with prenominal adjectives in the Buckeye corpus. The differences are significant: (a) χ2(1, N = 2172) = 66.731, p < 0.001; (b) χ2(1, N = 54) = 4.360, p < 0.037.

Second, as in Brown, the distributions of items like finite and unknown are significantly different across prenominal and non-prenominal environments, as in Table VIIIb. In prenominal position words like unknown represent 19% of adjectives with secondary stress, while in non-prenominal position they account for 32%. Resolvable clash is therefore also underrepresented in both corpora.
What we see then is that both unrepairable clash and repaired clash are underrepresented, in the written corpus as well as the spoken corpus. This means that there is more going on than just the avoidance of marked elements and configurations; phonological repair is also avoided.
Other explanations for these skewings are, of course, possible. One might suppose that the distribution of the four classes of adjectives is accidentally connected to the semantics, and that trochaic adjectives tend to have meanings more appropriate for prenominal position while iambic adjectives tend to have meanings more appropriate for other positions. There are at least three reasons to reject this kind of approach as an explanation. First, showing that there is a statistical correlation between semantic or syntactic categories and phonological properties is not itself an explanation. What we need is some explanatory principle and/or some grammatical mechanism that makes the connection necessary, and allows it to follow from general principles. Second, appeal to accidental semantic or syntactic biases is not a unified account. The account developed here involves a single explanatory principle that covers all cases. Finally, the account developed here is not only unified, but also sensible. It extends existing grammatical machinery in a straightforward way, rather than appealing to accidental semantic facts.Footnote 9
4 Morphological processes: mutation
In this section I turn to a rather different phenomenon, and show that Welsh mutation exhibits the opposite distribution from the English cases.
Let's review the general pattern. Welsh has three basic mutations. These are a class of consonantal changes that take place word-initially in a morphosyntactically prescribed set of environments. I focus on soft mutation, which involves the changes in (3).
-
(3)

Other consonants do not change in this environment. I call the changing consonants mutators; [f s χ n], etc. are non-mutators.
The examples in (4) show how this works. In (a), a feminine singular noun mutates after the definite article, and in (b) we see that an adjective modifying a feminine singular noun will also mutate. The object of certain prepositions mutates (c), as does the direct object of an inflected verb (d).
-
(4)

Hammond (Reference Hammond2014) demonstrates that Welsh mutation displays the opposite effect from what we saw in the previous section. This can be seen in the environment following prepositions that trigger soft mutation vs. all other environments. As mentioned above, certain prepositions, including those in (5), induce soft mutation in the following word.
-
(5)

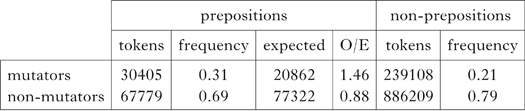
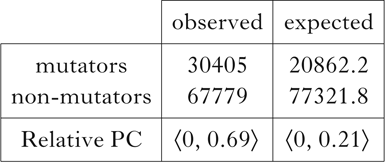
The CEG corpus (Ellis et al. Reference Ellis, O'Dochartaigh, Hicks, Morgan and Laporte2001) is a publicly available tagged corpus of written Welsh containing 1,223,501 words. In addition, it gives the lemma form for all tokens. In this corpus mutators constitute 21% of the total in other environments, but after prepositions that trigger soft mutation they form 31%, as in Table IX.
Table IX Distribution of words beginning with mutatable consonants (vs. others) after mutating prepositions (vs. other environments) in the CEG corpus. The difference is significant: χ2(1, N = 98184) = 5542.824, p < 0.001.
This means, that while we avoid both unresolvable and resolvable configurations in English stress clash, the opposite is true for Welsh soft mutation.
This is surprising, so let's make sure that it is correct. Personal names in Welsh do not undergo any of the mutations, as shown in (6a). This is not true for native and nativised geographic names, which can undergo the mutations, e.g. i Fanceinion [i vankejnjɔn] ‘to Manchester’ in (4c) above.
-
(6)

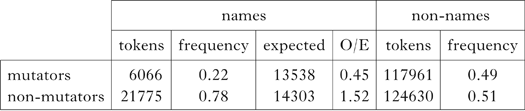
Consider now how often personal names begin with mutatable consonants. If mutation is avoided – like rhythm and clash in English – we would expect names to begin with mutatable consonants more often than non-names. In fact, the opposite is the case, consistent with the reversal we saw above in mutation contexts for non-names: names are less likely to begin with a mutatable consonant, as shown in Table X.Footnote 10
Table X Distribution of names beginning with mutatable or non-mutatable consonants (vs. non-names) in the CEG corpus. The difference is significant: χ2(1, N = 27841) = 8027.046, p < 0.001.
We might be concerned that the patterns could be different in spoken language. In fact, we observe a similar distribution in a spoken corpus. The Siarad corpus (Deuchar et al. Reference Deuchar, Davies, Herring, Parafita Couto, Carter, Thomas and Mennen2014) is a transcribed spoken corpus of approximately 607,450 words.Footnote 11 It is not tagged for part of speech, but the basic soft mutation comparison above can be approximated. I used only those prepositions triggering soft mutation that can be identified unambiguously, leaving aside i and o, which are ambiguous between preposition and pronoun. I then searched for all words that begin with sounds that unambiguously could either mutate or be mutated, setting aside vowel-initial words, since they can either be the mutated result of a [g]-initial word or a true vowel-initial word. This gives us the counts in Table XI, which can be compared to those in Table IX.
Table XI Distribution of words beginning with unambiguous mutatable consonants (vs. others) after unambiguous mutating prepositions (vs. other environments) in the Siarad corpus. The difference is significant: χ2(1, N = 6830) = 14.833, p < 0.001.
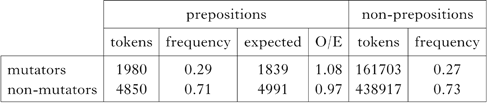
Words beginning with mutatable consonants are more likely after mutating prepositions. This difference is smaller than in the written corpus, but is also significant.Footnote 12 Hence we observe the same effect in the spoken register as well.
I conclude that mutation indeed exhibits the opposite distribution from the English cases considered in the previous section.
5 Analysis
In this section I provide an analysis for the facts considered above. Before proceeding, let us consider what has been established empirically.
First, underrepresentation of words like a′loof in prenominal position, [d] vs. [t] word-initially, [d] vs. [dr] word-initially, etc., shows that marked elements and configurations are statistically avoided. Second, underrepresentation of words like ˎun′known in prenominal position shows that the Rhythm Rule, a phonological change, is also avoided.
On the other hand, Hammond (Reference Hammond2014) shows that there is overrepresentation of mutatable consonants in mutation contexts in Welsh, the opposite from what we saw in English. This was confirmed here by showing that non-names vs. personal names in Welsh in the CEG corpus and the spoken Siarad corpus show the same reversal.
The first two cases above look rather like Lexicon Optimisation, and it would be reasonable to try to build an account in terms of the machinery involved in that approach.Footnote 13 Prince & Smolensky's (Reference Prince and Smolensky2004: 225–226) original definition is given in (7).
-
(7)

The basic idea is that if there are multiple ways to produce an output form consistent with the facts of a language, the input that produces the fewest constraint violations is chosen.
To see this in action, consider a simple example. Imagine we have nasal place assimilation, and a constraint against NC sequences with different place values which outranks the relevant faithfulness constraints. For heteromorphemic examples, we would have tableaux like (8).
-
(8)

Here we have an input /n/ which is realised as [m] before a labial. Because the example is heteromorphemic, we can assume that there are other contexts – perhaps vowel-initial – where we can determine that the prefix-final consonant is indeed /n/. However, there are tautomorphemic cases where the input is unknown. An output form [lʌmp] is consistent with the inputs /lʌmp/ and /lʌnp/. Either input produces the same output, as in (9).
-
(9)

In these cases, Lexicon Optimisation favours the input that produces the desired output most harmonically. We can see this in a ‘reverse tableau’, as in (10), where inputs are given along the left and the violations marked are those for the optimal candidate, given that input.Footnote 14 As far as possible, lexicon optimisation ensures that what you see is what you get.
-
(10)

There are, of course, no empirical consequences to Lexicon Optimisation in itself. In fact, it is defined to apply only when there are no consequences. I examine now whether it is profitable to view the underrepresentations we see in English as statistical analogues to Lexicon Optimisation.
To accommodate the effects we saw in English, we need to expand the notion of lexicon optimisation to accommodate comparisons between inputs when the outputs are not the same. To do this, let's first define a notion of p honological complexity that applies to individual input–output pairings but also to entire phonological systems. (The basic logic of this is that the complexity of a phonological system is proportional to the number of asterisks in its tableaux.) We first define the output/surface forms of a language as a possibly infinite set, as in (11a).
-
(11)

Every member of that set has a corresponding (optimal) input form (11b), and, for any phonology, there is also, of course a finite sequence or vector of constraints (11c).
Any input–output pairing ⟨I i , O i ⟩ (where angle brackets represent vectors) then defines a finite vector of violation counts, some number of violations for each constraint incurred by the winning candidate for that input, as in (12).
-
(12)

With these notions, Phonological Complexity is defined as in (13).
-
(13)

This can again be exemplified with our hypothetical nasal assimilation example. Let us assume the following set of forms whose PC we wish to compute. Given the inputs in (14), we have the constraint violations shown for the winning candidates.
-
(14)

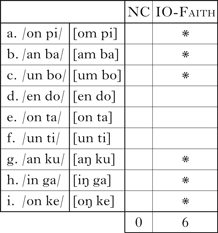
The relative complexity of this system is ⟨0, 6⟩/9 = ⟨0, 0.67⟩. We can compare the system in (14) with the one in (15). Here we have a different array of output forms, but the same logic for inputs and constraint violations.
-
(15)

The relative complexity of this second system is ⟨0, 4⟩/8 = ⟨0, 0.5⟩. The second system is less complex than the first: ⟨0, 0.5⟩ < ⟨0, 0.67⟩. It would be reasonable to assume that more complex complexity vectors should be compared using the logic of strict ranking, for example ⟨0.9, 0.5⟩ > ⟨0.4, 0.67⟩.
In the example above, the relative magnitude of the higher-ranked constraint determines the relative complexity of the systems, rather than the relative magnitude of the lower-ranked constraint.
The proposal then is that all phonological systems are skewed to be less complex, as determined by (16).
-
(16)

This alters the frequency of input–output pairings; it does not change the input representation of any particular form.
Let's examine each of the English cases. For word-initial [t] vs. [d] we assume there is a constraint penalising voiced stops: *VdStop. Imagine we have a sample of 100 words that begin with coronal stops with the distribution in (17a).
-
(17)

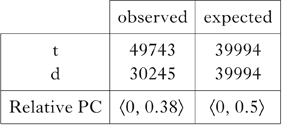
The total PC score is ⟨0, 50⟩, and the relative score ⟨0, 50⟩/100 = ⟨0, 0.5⟩. We can imagine a skewed distribution, of the sort we saw in English, but more extreme, like (17b). Here the total PC score is ⟨0, 25⟩, and the relative score ⟨0, 25⟩/100 = ⟨0, 0.25⟩. The latter distribution, with fewer word-initial instances of [d], is thus less complex. The actual occurring and expected distributions from the Brown corpus, along with relative PC scores, are given in Table XII.
Table XII Relative PC scores for word-initial [t] and [d] in the Brown corpus.
The same logic applies in the case of word-initial [d] vs. [dr], except that the relevant markedness constraint is *Complex. A distribution like (18a) is dispreferred to one like (18b).
-
(18)

As in the previous pair, the relative PC score for the less preferred distribution is ⟨0, 50⟩/100 = ⟨0, 0.5⟩, while that for the preferred distribution is ⟨0, 25⟩/100 = ⟨0, 0.25⟩. The latter distribution, with fewer word-initial instances of [dr], is less complex. The actual distribution and relative PC scores for the Brown corpus are given in Table XIII.
Table XIII Relative PC scores for word-initial [dV] and [dC] in the Brown corpus.
Prenominal ′happy vs. a′loof works exactly the same way with respect to the markedness constraint *Clash. Here, the higher-ranked constraint is not a faithfulness constraint, since we know stress shift is generally possible in English, but a constraint that requires that if stress shifts, it shifts to a syllable that would otherwise bear secondary stress. For convenience, we call this Secondary. The distribution in (19a) is less preferred than that in (19b).
-
(19)

The calculation is exactly the same. Actual values and relative scores from Brown are given in Table XIV.
Table XIV Relative PC scores for prenominal adjectives with unresolvable stress configurations in the Brown corpus.
Finally, consider the case of prenominal ′fiˎnite vs. ˎun′known. Here what is ruled out is application of the Rhythm Rule, not clash per se. We can assume that when stress shift applies, it violates some version of OO-correspondence, a constraint requiring stress in a clash context to be the same as stress in other contexts. That constraint, in turn, is dominated by *Clash, and of course by Secondary, as in (20).
-
(20)

Table XV gives the true values and relative scores from the Brown corpus.
Table XV Relative PC scores for prenominal adjectives with resolvable stress configurations in the Brown corpus.
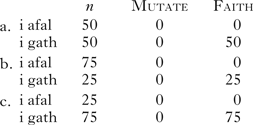
What about the Welsh examples? On the face of it, its looks as if Welsh is skewed so as to make its system more complex. Recall that in a mutation context, such as after a preposition like i, we find more instances of mutating consonants than in non-mutation contexts. Let's assume that there is a constraint that forces mutation in various environments; we can call it Mutate. This constraint outranks the relevant faithfulness constraint. We get exactly the wrong prediction when we consider the same two hypothetical distributions as in the previous cases. Compare mutating items like cath [kaːθ] ‘cat’ vs. non-mutating items like afal [aval] ‘apple’ after i. (21a) shows a neutral distribution, while what we would expect is fewer instances of constructions like i gath, as in (b) – we would then have ⟨0, 0.25⟩, rather than ⟨0, 0.5⟩. The problem is that we get just the opposite. In mutation contexts, we find more instances of constructions like i gath. Schematically, we have (21c), where we find ⟨0, 0.75⟩, rather than ⟨0, 0.5⟩, exactly the opposite of what is predicted by Input Optimisation (16).
-
(21)

Actual values and relative scores from the CEG corpus are given in Table XVI.
Table XVI Relative PC scores for mutatable vs. non-mutatable initial consonants in the CEG corpus.
Why might Welsh mutation behave in this way? The difference is apparently that mutation is a morphologically conditioned phonological change, so it seems reasonable to build an explanation on that difference. We can accommodate this under the Input Optimisation rubric if, in fact, there is a constraint favouring the expression of morphological categories. The logic is that the reason why mutatable consonants are overrepresented where they are is because there is a constraint that demands that morphological categories be expressed.
The key point is that mutation, whether phonological, morphological or lexical, must be subject to a constraint forcing morphological categories to be expressed. If mutation is indeed a morphologically conditioned phonological change, there is no issue. Some researchers (e.g. Stewart Reference Stewart2004, Green Reference Green2006, Hannahs Reference Hannahs, van Oostendorp, Ewen, Hume and Rice2011, Reference Hannahs2013) have argued that mutation systems should be treated morphologically or lexically, either in terms of some special class of morphological rules or in terms of listed allomorphs. If one of these is correct, then application of that morphological rule or selection of allomorphs must be subject to a constraint that requires morphology to be expressed. I will continue to describe mutation as a phonological process, but the general Input Optimisation account developed here is consistent with other views of mutation as well.
In fact, Kurisu (Reference Kurisu2001) proposes something close to what we need, in (22).
-
(22)

Soft mutation expresses morphological information. To the extent that a word in a soft mutation context begins with a mutatable consonant, violations of RM are avoided. Thus when a form like cath [kaːθ] undergoes soft mutation to become gath [gaːθ], RM is satisfied. When afal [aval] does not change in a soft mutation context, RM is violated.
If we add RM to the constraint set for Welsh and rank it above Faith, this accommodates both Welsh cases. Consider first mutatable vs. non-mutatable consonants in mutation contexts, the schematic example just considered. In (23a), mutators and non-mutators are relatively evenly distributed (note that Mutate is here for completeness). RM forces the category to be expressed, and higher-ranked Mutate forces the precise expression of that category.
-
(23)

The case in (23b) has proportionally more mutators. When relative PC is calculated with RM in the mix, we find the latter distribution is preferred: ⟨0, 0.5, 0.5⟩ > ⟨0, 0.25, 0.75⟩. This is, of course, also true for the actual distribution in the CEG corpus, where the occurring distribution ⟨0, 0.31, 0.69⟩ is preferred to the expected distribution ⟨0, 0.79, 0.21⟩. Notice that ranking, strict or otherwise, is key here. If RM is not ranked higher than Faith, we do not get the desired effect.
The effects of Input Optimisation are thus contingent on the ranking or weighting of the constraints in the language. Though the claim is that all languages will exhibit skewing to satisfy Input Optimisation, it does not follow that all languages will skew in the same way. Different weights or rankings will entail different skewings. Consider for example, the common loss of final syllables, even when they may be desinential, marking inflectional properties of the word in question. This is a purely phonological process that is not conditioned by the morphology. How is such a thing possible on the account here? Presumably there is a high-ranked/weighted constraint that favours the loss of such syllables and outranks RM. Input Optimisation will minimise violations of the higher-ranked/weighted constraints over those of lower-ranked/weighted constraints like RM. See §8 below for more discussion.
Consider now non-mutatable consonants in personal names vs. non-names: non-names begin with mutators more often than names do. If we take the distribution of mutators in names as the neutral distribution and the distribution with non-names as the distribution to be explained, this emerges directly: non-names have more mutators because that avoids violations of RM, just as in the examples considered above.
The RM constraint, however, is too restrictive. It would seem to imply that expression of a morphological category is minimal, that if it is already expressed elsewhere, there is no pressure to express it again. This in turn predicts that if mutation were to be triggered by an overt affix, then we should not see an overrepresentation effect.Footnote 15 In fact, such cases do occur in Welsh, and are predicted to show an overrepresentation effect as well.
There is a set of prefixes that trigger soft mutation in Welsh, e.g. cyn- [kɨn/kən] ‘ex-’, gor- [gɔr] ‘over-’, ail- [ajl] ‘re-’, di- [di] ‘-less’, hunan- [hɨnan] ‘self-’, is- [is] ‘sub-’, gwrth- [gurθ] ‘anti-’, cyd- [kɨd, kəd] ‘co-’, ad- [ad] ‘re-’, etc. The first three of these are exemplified in (24).
-
(24)

The examples above include stems that begin with mutators and those that begin with non-mutators. What is the distribution? Is it similar to what we see after prepositions or to what we see elsewhere? To test this, I found all instances of these prefixes in the CEG corpus marked with a hyphen, and then did counts on the following stems.
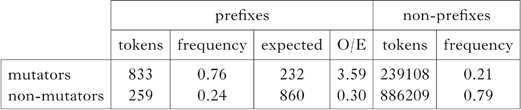
One small complication is that a hyphen is not generally required for these prefixes. I chose to count the ones marked with overt hyphens, as it is of course easier to find these in the corpus. However, the hyphen is required just in case there might be an orthographic ambiguity. This occurs when the final letter of the prefix and the first letter of the stem could be misparsed as part of the digraphs ll [ɬ] and dd [ð]. Thus a form like ail-lenwi [ajllεnwi] ‘refill’ must be spelled with a hyphen to avoid the double letters being misinterpreted as *[ajɬεnwi]. Including items of this sort would bias our counts in favour of mutators, so they were excluded. (This slightly biases the count against mutators.) We find the distribution in Table XVII, which can be compared with the distribution of mutation in the non-preposition environment from the CEG corpus in Table IX. I take the latter to be the default.
Table XVII Distribution of prefixed stems beginning with mutatable vs. non-mutatable consonants in the CEG corpus, as compared with unprefixed items. The difference is significant: χ2(1, N = 1092) = 1976.534, p < 0.001.
The effect is so large that we might worry that something else is going on, e.g. that word-internal mutation is subject to other pressures not yet considered, but similar effects have been found in Welsh for plural suffixation and various associated stem-vowel changes (Anderson Reference Anderson2015). At this point, we must conclude that the pressure to express some morphological category via some phonological process is not contingent on whether that category might also be expressed elsewhere by an independent word, like a preposition, or by another morpheme. In the case at hand, the relevant morphological category is expressed by both a prefix, e.g. ail-, and soft mutation. What is key is that soft mutation doesn't apply to the prefix itself, but to the following stem. As it stands, RM would not enforce both operations, since the prefix and the mutation are both in the same word. The RM constraint must therefore be revised so as to allow this. The key is to restrict the notion of ‘morphological form’ in (22) to just a morpheme, as in (25).
-
(25)

The revision is minimal, and accounts for all the cases treated so far, including the prefix example just considered. In the prefix case, there are two domains for RM′: the prefix itself and the stem. For a form like ail-fyw [ajlvɨw] above, we have ail [ajl] (*Ø) and fyw [vɨw] (*[bɨw]).
6 Confirmation
The solution developed in the previous section straightforwardly describes the cases we have considered, but relies on the assumption that it is morphology that behaves differently. It could just be that Welsh and English behave differently. In this section, this other possibility is ruled out by considering cases of morphologically triggered phonology in English and non-morphologically triggered phonology in Welsh.
Let's first look at an example in Welsh that is not connected to mutation. This example involves devoicing of voiced stops in the final coda of Welsh adjectives when they occur medially in comparatives and superlatives. The basic form of comparatives and superlatives is given in (26a), and (b) shows that if the stem ends in a voiced stop it devoices.
-
(26)

This is an unusual process, the reverse of the more usual sort of voicing alternation one might see in an case like this, i.e. final devoicing. The historical analysis of these is that, at some point, the suffixes could be analysed as *-hax and *-hav and the devoicing we see here is the residue of the effects of the [h] (Morris Jones Reference Morris Jones1913). Regardless of the history, the synchronic analysis must include some constraint or set of constraints that force this devoicing, and our interest is in whether Faith violations are minimised here by Input Optimisation.
This is a non-morphological process, in the sense that it does not involve a particular morphological category. Specifically, the comparative and superlative are marked by affixes, and devoicing is simply restricted to certain morphological contexts. See §8 below for more discussion.
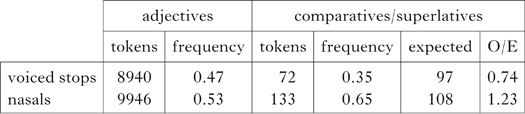
Let's now consider the distributions.Footnote 16 It turns out that word-final voiceless stops are extremely rare, so more accurate comparisons can be made if we use a different category as our comparison base: nasals. The CEG corpus is a written one, and there is an ambiguity in the Welsh orthography in terms of how to interpret ng (as [ŋ] or [ŋg]), so we only look at non-dorsals, comparing the distribution of stem-final [b d] with [m n]. In Table XVIII we see that voiced stops are underrepresented in comparatives and superlatives.
Table XVIII Distribution of stem-final [b d] and [m n] in unaffixed vs. comparative/superlative adjectives in the CEG corpus. The difference is significant: χ2(1, N = 205) = 12.269, p < 0.001.
This establishes that Welsh and English are not generally reversed. Hence Welsh adjectives behave like other English phonological examples.
We can look in the other direction as well. What about morphological cases in English? If the Input Optimisation with RM′ approach is correct, we expect them to behave like the Welsh soft mutation examples. English doesn't have anything like mutation, but does have morphological haplology (Stemberger Reference Stemberger1981, Menn & MacWhinney Reference Menn and MacWhinney1984, Zwicky Reference Zwicky1987). One example is the genitive plural in (27): the key fact is that overt plurals do not co-occur with the genitive.
-
(27)

Another example is the adverbial suffix -ly in (28): the suffix is not added to an adjective that already ends in ly.
-
(28)

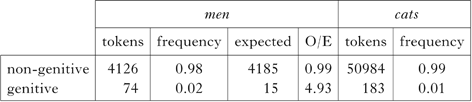
What we find in the Brown corpus is precisely what we would predict under Input Optimisation with RM′: forms like cats’ in the genitive plural are statistically underrepresented, as shown in Table XIX.
Table XIX Distribution of genitive and non-genitive plurals in terms of overt suffixation in the Brown corpus. The difference is significant: χ2(1, N = 4200) = 232.399, p < 0.001.
Similarly, Table XX shows that adverbs are much more frequent with adjectives that don't already end in -ly in the Brown corpus.
Table XX Distribution of adjectives and adverbs in -ly in the Brown corpus. The difference is significant: χ2(1, N = 951) = 202.629, p < 0.001.

One final example can be added here: word-final t/d-deletion. This is a well-known phenomenon, initially studied by Guy (Reference Guy1991) and more recently by Turton (Reference Turton2012) and Coetzee & Kawahara (Reference Coetzee and Kawahara2013). The basic effect is that word-final [t d] can be deleted word-finally in English, e.g. in friend [frεnd, frεn]. The process is governed by a number of factors, including whether the [t d] appears in a cluster, whether the following word begins with a vowel, speech rate, informality, lexical frequency, etc. The relevant factor here is that the process applies less readily if it would delete a consonant that is the sole exponent of the -ed past tense. Thus, all else being equal, we expect deletion to apply more readily to a word like text [tεkst, tεks] than a word like boxed [bakst, baks].
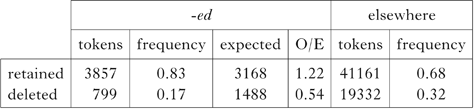
This is indeed the case in the Buckeye corpus. Table XXI shows the relative retention of final [t d] as a function of whether the word in question ends in -ed.
Table XXI Distribution of [t d] deletion in suffixed vs. unsuffixed forms in the Buckeye corpus. The difference is significant: χ2(1, N = 4656) = 468.807, p < 0.001.
The facts of t/d-deletion are consistent with the account given here, and support the hypothesis that a skewing reversal occurs when RM′ would apply. We would expect deletion to be underrepresented just in case it would violate RM′, and that is what we see here. The Input Optimisation account is then an alternative to the rule-based and constraint-based stratal approaches of Guy (Reference Guy1991) and Turton (Reference Turton2012) respectively.
Hence adjective devoicing in Welsh, the genitive plural in English, adverbs in English and t/d-deletion in English work just as would be predicted if the relevant distinction is morphological expression vs. phonological generalisations.
Since adjective devoicing in Welsh is not a morphological operation like lenition, it does not incur violations of RM′. Therefore faithfulness violations are minimised, and we expect underrepresentation of forms that would otherwise undergo devoicing. The genitive plural in English is an overt affix, and thus clearly involves a morphological operation governed by RM′. Hence we expect underrepresentation of the haplological cases, as we find. Adverbs in English work the same way. RM′ favours expression of the adverbial suffix, so we expect to find underrepresentation of the haplological cases. In the case of deletion of [t d], we see a case where a normal phonological process is limited by RM′.
7 How does Input Optimisation work?
We have established a number of frequency effects that can all be unified and accommodated under the principle of Input Optimisation (16), but how does it work concretely? Here we address two questions. First, where does Input Optimisation take place? Is it a part of grammar, or something else? Second, wherever it may ‘live’, why doesn't it overpower the rest of the grammar? The ideas in this section are extremely speculative, but are intended to lay the groundwork for future research.
We need to clarify two important aspects of the proposal. First, Input Optimisation does not entail that all languages work the same way. We've seen that it works to minimise constraint violations across the language, and that it is sensitive to constraint ranking or weighting. Given that violations of higher-ranked or weighted constraints will be minimised over violations of lower-ranked or weighted constraints, and given that weight/ranking is at least partially language specific, it follows that the effects of Input Optimisation will differ across languages.
Second, Input Optimisation is a global effect, beyond the lexicon. We've seen a number of cases where Input Optimisation might be taken as an effect in the lexicon, some mechanism by which the number of words that fit some phonological requirement are more or less than expected. However, two facts militate against an exclusively lexical account. First, all of our counts have been from corpora, not dictionaries. That is, we are explicitly considering how often words and constructions are used, rather than how often words occur in a dictionary. Second, as just noted, we've also seen a number of cases where it is phrases or multi-word patterns that are skewed. Assuming that phrases are not generally listed lexically, this argues against attributing Input Optimisation exclusively to the lexicon. One might counter that the statistical combinatory properties of lexical items can be stored in the lexicon, and this is certainly true, but this amounts to extending our notion of the lexicon to include statistical syntactic properties.
Given that Input Optimisation extends beyond the lexicon, there are at least four ways we might think of it: (i) as an historical effect, (ii) as a property of acquisition, (iii) as a performance constraint or (iv) as evidence for a different kind of phonological architecture. The first two are related, as are the last two. I treat each of these four in turn.
Input Optimisation could be specifically a property of historical change. That is, there is pressure for historical change to selectively reduce the phonological complexity of the system as a whole. The basic idea is that Input Optimisation is a mechanism of historical change, and that the effects we have seen are not enforced by the grammar, but are the result of historical accretion. This is a reasonable approach. Historical change is often a by-product of the acquisition process, so we would have to carefully distinguish this from a purely acquisition-based account (see below). We would also need to think carefully about the phrasal skewings we've seen, and would have to allow for historical changes that change how often various words might co-occur.
Another possibility, related to the historical approach, is to view Input Optimisation as a property of acquisition. This approach assumes that the acquisition process is biased to minimise phonological complexity. Again, the effects we see would be a consequence of changes that occur during acquisition, not enforced by the adult grammar per se. If this were true, this would certainly have consequences in the historical domain, but we could in principle distinguish the two views. There are historical changes that occur in adult speech. If Input Optimisation were an acquisition effect, then we would expect those adult changes not to be biased by it, and we would also expect to see Input Optimisation imposed by the child during acquisition.
Yet another interpretation of Input Optimisation would be as a performance effect, in which the performance module filters the output of the grammar so as to satisfy Input Optimisation. Viewing performance as a filter begs questions of teleology, but these are the same questions begged by any theory that includes constraints on the output. We might distinguish this approach from the preceding ones with psycholinguistic experiments that tap into language processing, as opposed to grammatical structure. To the extent that we can determine different effects for the grammar and the performance system, and that Input Optimisation is localised to the latter, this would be evidence a view like this.
Finally, we might view Input Optimisation as part of the grammar itself. On this view, it would be an output condition on the entire grammar, as a general phonological sieve. This would require: (i) that the phonology itself be probabilistic in nature, an approach currently adopted in a number of areas of the field (see e.g. Boersma Reference Boersma1997, Hammond Reference Hammond, Darnell, Moravcsik, Newmeyer, Noonan and Wheatley1999, Reference Hammond, Carnie, Harley and Willie2003, Coetzee Reference Coetzee2008, Hayes & Wilson Reference Hayes and Wilson2008, Pater Reference Pater2009, Coetzee & Pater Reference Coetzee, Pater, Goldsmith, Riggle and Yu2011), and (ii) that the phonology be able to constrain the syntax, morphology and lexicon of a language. This, of course, raises the same teleological questions as above, but they are again the same as any framework that includes constraints.
The data presented here do not distinguish among these choices, but hopefully it is clear what kinds of further empirical investigations might. Do we see effects of Input Optimisation in acquisition? Do we see effects of Input Optimisation in adult change? Can we distinguish Input Optimisation in competence vs. performance?
Let's now turn to the second question. Why does Input Optimisation not go all the way, eliminating any constraint violation? There are two reasons: constraint ranking (or weighting) and the overall functionality of the system.
In a system with weighted or ranked constraints, it may be impossible in some cases to minimise violations of one constraint without simultaneously maximising violations of another, as in (29).
-
(29)

Here we might minimise candidates like y, maximising candidates like z. The effect would be a less complex system, but it would not be a system free of violations.
We can imagine other configurations though. Recall the hypothetical systems in (14) and (15). We saw how Input Optimisation would favour the second system over the first. The relative complexity of the first system is ⟨0, 6⟩/9 = ⟨0, 0.67⟩, and that of the second ⟨0, 4⟩/8 = ⟨0, 0.5⟩. If this is so, we might well imagine that the system could go even further, as in (30).
-
(30)

Here no constraints are violated, so the system is the minimally complex: ⟨0, 0⟩. The effect is to reduce the inventory of nasals and stops in this environment to just those that do not violate NC or IO-Faith.
But a system that allows free rein to Input Optimisation is one where no constraints are violated; effectively only one word is possible, composed of maximally unmarked segments in an optimal prosodic and segmental configuration: [ta] (or something similar). The reason then that Input Optimisation does not have this effect is that it is offset by the need to have a sufficiently large set of morphemes and a sufficiently large array of combinatory possibilities to make communication possible. I therefore propose (31) as a counterforce to Input Optimisation.
-
(31)

Conceptually, this does the trick, as it balances Input Optimisation against the functionality of the system. Clearly, however, though it captures the logic of the situation, it is still quite speculative. Turning this into something more concrete requires an investigation into the morphosyntax and semantics of a language. It would also be important to put it into explicitly quantitative terms, so it can be tested statistically. I leave this to further research.
8 Morphology and phonology
The RM′ constraint in (25) requires that we be able to distinguish morphological processes like Welsh mutation from phonological processes like English nasal assimilation. There are a number of ways we might do this, but (32) seems the clearest.
-
(32)

Note that, on this definition, a morphological process is not simply one that has morphological conditioning. As we will see, a process might very well be restricted to some morphological context, and not meet the definition set by (32). The definition is then not about how the process might be formalised, but about what role it plays in the morphological system. Let's go through all the cases consider thus far and show how they fit or do not fit this rubric.
First, the English cases we considered in §2 involving segmental and phonotactic markedness do not qualify, because they are not morphologically restricted; hence they never mark some morphological category.
The English rhythm example treated in §3 also does not qualify, for the same reason. It is not morphologically conditioned, and thus never marks some particular morphological category. There is a different stress alternation in English that does sometimes mark morphology, the shift of stress to the left in the Latinate vocabulary when certain verbs undergo zero-derivation to become nouns, illustrated in (33) (Chomsky & Halle Reference Chomsky and Halle1968, Hayes Reference Hayes1980, Kiparsky Reference Kiparsky1982).
-
(33)

This is a different process, however. It only affects a small set of items of Latin origin, it only applies to nouns and it is not subject to the restriction that there must be a secondary to the left.
The Welsh mutation facts treated in §4 do qualify as a morphological process. Mutation is restricted to specific morphological environments, and there are environments where mutation is the sole marker of some morphological category. One environment for this is after the possessive ei ‘his, hers’. Without the optional following echoing pronoun, the sole marker of the gender difference is the mutation triggered by the possessive. In the case of the masculine form we have soft mutation, and in the case of the feminine we have aspirate mutation. Thus, for example, ei mam [i mam] can only mean ‘her mother’, since mam ‘mother’ does not undergo mutation. Similarly, ei fam [i vam] can only mean ‘his mother’, since mam does undergo soft mutation.
The final consonant devoicing treated in §6 does not qualify as morphological on this definition. While the process is restricted to particular morphological contexts, it never occurs without some other overt marker of that morphological context. The devoicing is never the sole marker of the comparative or superlative form.
The English haplology cases we saw in the same section are clearly morphological. These cases involve the presence or absence of a morpheme, which can be the sole marker of the respective morphological category, e.g. man vs. man's and wrong vs. wrongly.
Finally, the deletion of final coronal stops in English is clearly morphological in the sense intended when it deletes the past tense marker, e.g. look vs. looked.
There are, of course, other ways we might do this, but (32) is simple and captures the intuition that a process is morphological when, in at least some context, it affects whether some morphological category is expressed.
9 Conclusion
There are always alternative analyses available, and this is especially true for statistical analyses. The skewings observed above are consistent with any number of syntactic, lexical or semantic explanations. For example, the set of adjectives that can be made into comparatives or superlatives in Welsh could be semantically skewed. Alternatively, some of these skewings could be statistical accidents – patterns that are statistically unlikely, but have arisen by chance. The argument offered here is that we can unify all these under a single theoretical characterisation, rather than treating them as a collection of unconnected explanations and appealing to chance. In addition, our account makes clear predictions about other systems, predictions not made by an approach that treats these effects as unconnected or arising by chance.
The proposal in this paper does not come out of the blue. Similar ideas have been put forward in the literature, but none of these have the same empirical coverage as Input Optimisation.
One idea that bears some similarities is the idea that markedness correlates with number of violations (Golston Reference Golston1998, Coetzee Reference Coetzee2008). Input Optimisation takes this several steps further by allowing application of this to faithfulness, and by allowing it to alter distributions.
The notion of using Lexicon Optimisation to alter distributions is presaged in diachronic restructuring contexts by Bermúdez-Otero (Reference Bermúdez-Otero1998).
The idea that the frequency of forms is governed by constraint weights is also pursued by Hayes & Wilson (Reference Hayes and Wilson2008). Their approach uses the distributions to fix the weights. The approach here uses the categorical phonology to determine the weights and then uses those weights to determine the distribution.
Input Optimisation is explicitly introduced in Hammond (Reference Hammond2013, Reference Hammond2014). The former identifies the effect for phonological markedness and faithfulness; the latter first observes the challenge posed by Welsh mutation and suggests a solution using RM. In this paper, these ideas have been taken further by demonstrating that the empirical contrast between mutation and the initial English cases is indeed based on the morphological nature of mutation. This was done by analysing the English haplology examples, the Welsh stem-final devoicing examples, and English t/d-deletion. It has also been demonstrated here that RM must be revised as RM′, that some form of ranking is necessary to accommodate the RM′ examples and that PC must be assessed using some form of constraint ranking or weighting.Footnote 17
There are, of course, questions still to answer. One concerns the precise nature of morphology appealed to in the RM′ constraint. It is fairly clear from the extensive literature on mutation that it is morphological in nature. In fact, some have argued that it is no longer phonology at all. That said, a more precise characterisation of the difference between morphological processes that are subject to RM′ and phonological processes that are not would be a step forward.
A second question is how much under- or overrepresentation should occur in relevant cases. This paper assumes that a significant difference in distributions is what Input Optimisation predicts, but this establishes only a lower bound. The working hypothesis is that under- and overrepresentation are bounded by other modules of the grammar, and that the system will under- or overrepresent in conformity with Input Optimisation, up to the limits imposed outside the system.
For example, we've seen that constructions like i afal [i aval] are underrepresented compared to constructions like i gath [i gaːθ]. Crudely speaking, one can assume that this underrepresentation is bounded by the need to have vowel-initial words for things like apples (size of vocabulary and what phonological contrasts are available) and the need to talk about apples (what kinds of circumlocutions are available). These other aspects of the larger phonological and linguistic system are well beyond the scope of this paper, but are an obvious place to look in the future.