1 Introduction
Typological literature in phonology has long revolved around the question of which factors influence the observed typology. Two major lines of thought have emerged in this discussion: the analytic bias approach and the channel bias approach (Moreton Reference Moreton2008, Yu Reference Yu2013b).Footnote 1 The analytic bias approach argues that the observed typology results primarily from differences in the learnability of phonological processes; the channel bias approach argues that the inherent directionality of sound changes based on phonetic precursors (articulatory and perceptual) shapes typology (for further discussion, see Hyman Reference Hyman1975, Reference Hyman, Hume and Johnson2001, Greenberg Reference Greenberg, Greenberg, Ferguson and Moravcsik1978, Ohala Reference Ohala, Masek, Hendrick and Miller1981, Reference Ohala and MacNeilage1983, Reference Ohala and Jones1993, Kiparsky Reference Kiparsky and Goldsmith1995, Reference Kiparsky2006, Reference Kiparsky and Good2008, Blevins Reference Blevins2004, Moreton Reference Moreton2008, Reference Moreton2012, Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb, de Lacy & Kingston Reference de Lacy and Kingston2013, Garrett & Johnson Reference Garrett and Johnson2013, Cathcart Reference Cathcart2015, among others).
Empirical evidence often supports both approaches equally well. Typologically rare processes have in many cases been shown to be more difficult to learn, which supports the analytic bias approach (Kiparsky Reference Kiparsky and Goldsmith1995, Reference Kiparsky2006, Reference Kiparsky and Good2008, Wilson Reference Wilson2006, Becker et al. Reference Becker, Ketrez and Nevins2011, de Lacy & Kingston Reference de Lacy and Kingston2013, White Reference White2017; for an overview of the experimental analytic bias literature, see Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb). On the other hand, typologically frequent processes are often shown to directly result from the phonologisation of underlying articulatory or perceptual phonetic precursors (e.g. sound change in progress that results in a typologically common pattern), whereas rare or unattested processes lack such precursors, lending support to the channel bias approach (cf. Hyman Reference Hyman1975, Greenberg Reference Greenberg, Greenberg, Ferguson and Moravcsik1978, Ohala Reference Ohala, Masek, Hendrick and Miller1981, Reference Ohala and MacNeilage1983, Reference Ohala and Jones1993, Lindblom Reference Lindblom, Ohala and Jaeger1986, Barnes Reference Barnes2002, Blevins Reference Blevins2004, Reference Blevins2006, Reference Blevins2007, Reference Blevins, Willems and Cuypere2008a, b; see Garrett & Johnson Reference Garrett and Johnson2013 for an overview of the literature). This ambiguity of evidence poses the primary challenge in typological research.
The stance of this paper is that the typology is influenced by both factors (as has been argued in a growing body of recent research; see Hyman Reference Hyman, Hume and Johnson2001, Myers Reference Myers2002, Moreton Reference Moreton2008, Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb, de Lacy & Kingston Reference de Lacy and Kingston2013). However, the role of phonological research is to quantitatively evaluate which aspects of typology are more likely to result from one factor or the other. The question that this paper addresses is whether some observed typological distributions (e.g. those targeting the feature [voice]) are primarily influenced by different degrees of the learnability of different processes or by the different diachronic trajectories underlying different processes. In particular, this paper proposes a technique based on which channel bias influences on typology can be estimated.
1.1 Analytic bias
If typologically infrequent processes are experimentally shown to be more difficult to learn than typologically frequent processes (for an overview, see Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb), a reasonable conclusion would be that typological differences result precisely from these differences in learnability. A challenge that the analytic bias approach faces is that artificial grammar learning experiments frequently show no learnability differences between typologically rare or non-existent unnatural processes and typologically frequent natural processes when the structural complexity of the tested alternations is controlled for. The influences of analytic bias can be subdivided into substantive bias and complexity bias (Wilson Reference Wilson2006, Moreton Reference Moreton2008, Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb). For substantive bias, phonetically motivated processes are easier to learn than unmotivated (or unnatural) ones; for complexity bias, alternations involving more conditioning features are more difficult to learn than simpler alternations (Moreton Reference Moreton2008). A survey of experimental literature on analytic bias in Moreton & Pater (Reference Moreton and Pater2012a, Reference Moreton and Paterb) shows that there exist consistent differences in experimental results testing the two biases. While complexity bias was consistently confirmed by the majority of studies surveyed, experimental outcomes of the substantive bias were mixed. Several studies that tested the learning of unnatural alternations as defined in §2 found no effect of substantive bias (Pycha et al. Reference Pycha, Nowak, Shin and Shosted2003, Seidl et al. Reference Seidl, Buckley and Cristià2007, Kuo Reference Kuo2009, Skoruppa & Peperkamp Reference Skoruppa and Peperkamp2011, Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb, Do et al. Reference Do, Zsiga and Havenhill2016, Glewwe Reference Glewwe2017, Glewwe et al. Reference Glewwe, Zymet, Adams, Jacobson, Yates, Zeng and Daland2018). A smaller subset of studies, however, do report positive results (Carpenter Reference Carpenter2006, Reference Carpenter2010, Wilson Reference Wilson2006).
L1 acquisition and L2 acquisition of word-final stops by speakers of L1s that ban obstruent codas are the only areas where differences between the natural and unnatural pair of alternations are observed. Learners acquire word-final voiceless stops earlier than voiced stops, and devoice voiced stops more frequently than they voice voiceless stops word-finally (Clark & Bowerman Reference Clark, Bowerman, Fishman, Tabouret-Keller, Clyne, Krishnamurti and Abdulaziz1986, Kong et al. Reference Kong, Beckman and Edwards2012 and references therein; for an overview, see Broselow Reference Broselow, Hyman and Plank2018). It is likely, however, that this type of experiment tests differences in the learning of more complex vs. less complex articulations (Kong et al. Reference Kong, Beckman and Edwards2012), and not the abstract phonological learning that is observed, for example, in artificial grammar learning experiments (e.g. where complex alternations are more difficult to learn than simple alternations, which is independent of articulatory factors; Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb). Articulation of segments that require more articulatory effort in a given position is expected to be learned less successfully: ‘cross-language differences in the age of children's mastery of adult-like voiced stops are typically explained in terms of the relative difficulty of the laryngeal gestures for the language's voice onset time distributions’ (Kong et al. Reference Kong, Beckman and Edwards2012: 725). The identical mechanism is in fact responsible for final voicing within the channel bias approach: even adult L1 speakers with full contrast devoice final voiced stops gradiently and passively, due to their greater articulatory complexity, which can result in a typologically common sound change that operates in an adult population (cf. Labov Reference Labov1994). These L1 and L2 learning differences thus likely reflect differences in articulatory effort that should be modelled as a channel bias influence. It is in fact not trivial to show how differences in L1 articulatory learning would result in phonological typology (cf. Rafferty et al. Reference Rafferty, Griffiths and Ettlinger2013), given that, after some developmental stage, children reproduce their input with a high degree of faithfulness (e.g. in the acquisition of the voicing contrast; see Kong et al. Reference Kong, Beckman and Edwards2012).
1.2 Channel bias
One of the objections to the channel bias approach to typology is that it fails to explain why some processes are unattested (Kiparsky Reference Kiparsky2006, Reference Kiparsky and Good2008, de Lacy & Kingston Reference de Lacy and Kingston2013). Kiparsky (Reference Kiparsky2006), for example, lists several diachronic trajectories that would lead to final voicing, yet final voicing is arguably not attested as a productive synchronic process. More generally, combinations of sound changes could conspire to yield a number of processes that are never attested as productive synchronic alternations. In the absence of a diachronic explanation, Kiparsky invokes grammatical constraints and learnability to explain these typological gaps.
Most of the current models of typology within the channel bias approach are indeed insufficient for explaining such typological gaps, because they do not quantify the probability of the occurrence of sound changes or combinations of sound changes. The default explanation within the channel bias approach has long been a qualitative observation that common processes are frequent because they are produced by frequent sound changes or because they require fewer sound changes (Blevins Reference Blevins, Honeybone and Salmons2015: 485; also Greenberg Reference Greenberg, Greenberg, Ferguson and Moravcsik1978: 75–76). Such reasoning does not provide sufficient outputs for a quantitative comparison of different influences on phonological typology.
Despite these objections, mechanisms exist within the channel bias approach to derive typology that go further than the simple statement that rare sound changes produce rare alternations. Based on a typological study of an unnatural process, postnasal devoicing, Beguš (Reference Beguš2019) argues that unnatural processes require at least three sound changes (as opposed to at least two for unmotivated processes and at least one for natural processes; the Minimal Sound Change Requirement), which explains the relative rarity of processes with different degrees of naturalness. The idea that unmotivated processes are rare because they require a complex history is certainly not new (Bell Reference Bell1970, Reference Bell1971, Greenberg Reference Greenberg, Greenberg, Ferguson and Moravcsik1978: 75–76, Cathcart Reference Cathcart2015, Morley Reference Morley2015), but the Minimal Sound Change Requirement explains why unnatural processes are the least frequent (compared to natural or unmotivated processes; see §2). The Minimal Sound Change Requirement on its own, however, does not explain why some unnatural processes are attested, while others are not. To quantify the channel bias influences on typology further, the concept of the Minimal Sound Change Requirement has to be combined with the estimation of probabilities of individual sound changes that are required for each synchronic alternation to arise.
Two models have thus far attempted to quantify probabilities of the occurrence of various primarily static phonotactic processes and explain the relative rarity of some processes based on diachronic factors. Bell (Reference Bell1970, Reference Bell1971) and Greenberg (Reference Greenberg, Greenberg, Ferguson and Moravcsik1978) propose a ‘state-process model’. Their model operates with typological states (phonological, morphological and syntactic) that can arise from other states, depending on the number of previous states, transitional probabilities from one state to another and the rest probabilities of each state. This approach is most suitable for modelling the probabilities of various phonotactic restrictions. Modelling the probabilities of transitions (processes) in the version of the model in Bell (Reference Bell1971) involves relative probabilities that only tangentially reflect the frequencies of the processes in the samples. The main ideas behind Bell's and Greenberg's models are similar to what will be proposed in this paper, but their proposal lacks inferential statistical tests. Crucially, by estimating uncertainty behind the distributions with bootstrapping, we can compare the historical probabilities of alternations, and perform hypothesis testing on the comparisons. The proposal here also uses substantially more elaborate historical samples.
A different model for calculating the probabilities of the combination of sound changes is offered by Cathcart (Reference Cathcart2015), who computes permutations of sound changes that lead to a certain process (in this case, final voicing), and compares that to permutations of all sound changes in a given survey to gain an estimate of the probability of certain processes. Due to its design, however, Cathcart's (Reference Cathcart2015) model relies on the representativeness of diachronic surveys for all sound changes, not only for those that are estimated (see also §3.2), and is computationally demanding, making it difficult to implement. The models in Greenberg (Reference Greenberg, Greenberg, Ferguson and Moravcsik1978) and Cathcart (Reference Cathcart2015) also do not take into consideration the crucial distinctions made in Beguš (Reference Beguš2019: 744): ‘the subdivision of unusual rules into unnatural versus unmotivated rules, paired with the proof that the latter require at least three sound changes to arise’.Footnote 2 The model proposed in this paper has the disadvantage that the trajectories of sound changes that lead to a certain alternation need to be identified manually (similar to the Bell and Greenberg models), but this also means that samples of sound changes need be representative only for the sound changes being estimated.
1.3 Objectives
The goal of this paper is to propose a quantitative method for estimating the influences of channel bias on phonological typology using a statistical method called bootstrapping (Efron Reference Efron1979, Efron & Tibshirani Reference Efron and Tibshirani1994). The technique estimates the historical probability, the probability of an alternation arising based on two diachronic factors: the number of sound changes required for an alternation to arise (the Minimal Sound Change Requirement; §2), and their respective probabilities, estimated from surveys of sound changes. Using the proposed technique, we can (i) estimate the historical probability of any alternation (§4), (ii) compare two alternations, attested or unattested, and perform statistical inferences on the comparison (§5.2) and (iii) compare outputs of the historical model with independently observed typology to evaluate the performance of the channel bias approach (§5.3). The assumptions of the model are discussed in §3.3. The paper also identifies mismatches between typological predictions of the analytic and channel bias approaches (§5.3 and §6). By testing these mismatched predictions against the observed typology, we can at least partially control for one factor when testing the other, and vice versa, which allows for quantitative evaluation of the distinct contributions of the analytic bias and channel bias factors to phonological typology (§6).
While the proposed method can be applied to any natural–unnatural pair of alternations, the paper focuses on a subset of typology: three natural–unnatural alternation pairs that target feature [±voice]. We estimate the historical probabilities of postnasal voicing (e.g. /p/ → [b] / m _) and postnasal devoicing (/b/ → [p] / m _), intervocalic voicing (/p/ → [b] / V_V) and intervocalic devoicing (/b/ → [p] / V_V), and final devoicing (/b/ → [p] / _#) and final voicing (/p/ → [b] / _#). The feature [±voice] is chosen because phonetic naturalness is probably best understood precisely for this feature (see Ohala Reference Ohala and MacNeilage1983, Reference Ohala2011 and Westbury & Keating Reference Westbury and Keating1986 on the ‘Aerodynamic Voicing Constraint’, and for detailed argumentation Beguš Reference Beguš2019), and all alternations have been well researched typologically. The alternations also differ in their degree of synchronic attestedness (see Fig. 3 below), providing a good basis for a comparison of different approaches to phonological typology.
2 Background
This paper makes use of several diachronic concepts from Beguš (Reference Beguš2019). First, it adopts the division of phonological processes into natural, unmotivated and unnatural. Natural processes, such as postnasal and intervocalic voicing and final devoicing, represent phonetically well-motivated universal phonetic tendencies. Unmotivated processes lack phonetic motivation, but do not operate against universal phonetic tendencies, which are defined by Beguš (Reference Beguš2019: 691) as ‘phonetic pressures motivated by articulatory or perceptual mechanisms … that passively operate in speech production cross-linguistically and result in typologically common phonological processes’. An example of an unmotivated process would be Eastern Ojibwe ‘palatalisation’ of /n/ to [ʃ] before front vowels (Buckley Reference Buckley2000). Unnatural processes not only lack phonetic motivation, but also operate against universal phonetic tendencies. Examples of unnatural alternations that operate against universal phonetic tendencies include postnasal devoicing, intervocalic devoicing and final voicing, which will be discussed in this paper.
We limit the modelling of sound change to a non-analogical phonetically driven sound change that targets a single feature value (Hyman Reference Hyman and Juilland1976). We also assume that a single sound change is a change of a single feature or a deletion of a feature matrix (the ‘minimality principle’; Picard Reference Picard1994). That a single sound change targets only one feature value is, at least in the great majority of cases, suggested by historical typology. Phonetic precursors also support the minimality principle: phonetic precursors that lead to sound change are usually articulatorily and perceptually minimal (Moreton Reference Moreton2008). For discussion, see Donegan & Stampe (Reference Donegan, Stampe and Dinnsen1979), Picard (Reference Picard1994) and Beguš (Reference Beguš2019).
This paper adopts two diachronic concepts for the derivation of typology within the channel bias approach that are proposed in Beguš (Reference Beguš2019): the Blurring Process and the Minimal Sound Change Requirement. Typological surveys of unnatural processes targeting the feature [voice] conducted in Beguš (Reference Beguš2018, Reference Beguš2019) and Beguš & Nazarov (Reference Beguš and Nazarov2018) identify thirteen languages in which postnasal devoicing has been reported either as a productive synchronic alternation or as a sound change. Based on this typological survey, a hypothesis about how unnatural processes arise diachronically is proposed: the Blurring Process, which states that unnatural alternations arise through a combination of a specific set of three natural (phonetically motivated) sound changes: (i) a sound change that leads to complementary distribution, (ii) a sound change that targets changed or unchanged segments in complementary distribution and (iii) a sound change that blurs the original complementary distribution (Beguš Reference Beguš2019). For example, postnasal devoicing results from three sound changes: (i) frication of voiced stops except postnasally ([b] > [ꞵ] / [―nas] _), (ii) unconditioned devoicing of voiced stops ([b] > [p]) and (iii) occlusion of voiced fricatives ([ꞵ] > [b]) (see §4.1).
This allows us to maintain the long-held position that sound change can only be acoustically or perceptually motivated (Garrett & Johnson Reference Garrett and Johnson2013, Garrett Reference Garrett, Bowern and Evans2015; for a discussion, see Beguš Reference Beguš2019).Footnote 3 This position is challenged by Blust (Reference Blust2005), who lists a number of unnatural sound changes. If, however, these unnatural sound changes result from combinations of natural sound changes (as argued by Beguš Reference Beguš2018, Reference Beguš2019 and Beguš & Nazarov Reference Beguš and Nazarov2018), we can maintain the position that sound change is always phonetically motivated.
Unnatural alternations thus cannot arise from a single sound change. Beguš (Reference Beguš2019) additionally argues that unnatural segmental alternations cannot arise from two sound changes either. If a change from ‘+’ to ‘―’ for a given feature [F1] is unnatural and therefore cannot result from a single sound change, some other feature ([F2]) has to change first, so that the change from [+F1] to [―F1] might be natural and motivated. For the full unnatural process to take place, however, that other feature ([F2]) has to change back to its original value. No such requirement exists for unmotivated processes: they can be the result of two sound changes. In sum, the Minimal Sound Change Requirement states that a minimum of three sound changes are required for an unnatural alternation to arise, a minimum of two sound changes for an unmotivated alternation and a minimum of one sound change for a natural alternation (see Beguš Reference Beguš2019).Footnote 4
3 Bootstrapping in order to estimate historical probabilities
The goal of this paper is to develop a model that will provide a quantification of probabilities of natural, unmotivated and unnatural processes which goes beyond the statement that natural processes are the most frequent, unmotivated less frequent and unnatural the least frequent. We can combine the Minimal Sound Change Requirement with the assumption that the probabilities of sound changes influence the probabilities of synchronic alternations. The probability that an alternation arises based on diachronic factors depends both on the number of sound changes that are required for the alternation to arise and on the probability of each individual sound change in the combination. Such probabilities are called historical probabilities (Pχ).
I propose that historical probabilities can be estimated with bootstrapping. Bootstrapping is a statistical technique within the frequentist framework for estimating sampling distribution (and consequently standard errors and confidence intervals for a statistic of interest) by random sampling with replacement (Efron Reference Efron1979, Efron & Tibshirani Reference Efron and Tibshirani1994, Davison & Hinkley Reference Davison and Hinkley1997).
3.1 The model
3.1.1 Individual sound changes
Probabilities of individual sound changes are estimated from a sample of successes (languages in a sample with a sound change Si) and failures (languages in a sample without the sound change Si), according to (1). If an alternation Ak requires only one sound change to arise and invariably occurs as a result of that change (i.e. Ak is natural), then we estimate its Pχ as in (1).
-
(1)

To estimate the historical probability of a sound change using the bootstrapping technique, we create samples from counts of languages (see §4.2). Languages with a sound change are treated as successes (coded as 1); languages without it as failures (coded as 0). The main advantage of the bootstrapping technique is that it estimates the confidence intervals of a historical probability. To estimate confidence intervals, we sample from this distribution of successes and failures 10,000 times (using ‘sampling with replacement’; Efron Reference Efron1979, Reference Efron1987). Each of these 10,000 samples is a probability of a success based on (1) (i.e. the proportion of 1s relative to 0s in the sample). These 10,000 probabilities constitute a sampling distribution, based on which standard errors and confidence intervals are calculated.
For example, when estimating the historical probabilities of processes targeting feature [voice], the successes and sample sizes are taken from surveys of sound changes (for exact counts, see §4.2). Sample sizes in our case range from 88 to 294, depending on the sound change (see §4.2). This repeated sampling with replacement yields a sampling distribution of historical probabilities: 10,000 data points for each process. From this sampling distribution, standard error, bias and 95% adjusted bootstrap (BCa) confidence intervals (CIs) that adjust for bias and skewness (Efron Reference Efron1979, Reference Efron1987) are computed.
The computation is implemented in the statistical software R (R Core Team 2016) with the boot package (Davison & Hinkley Reference Davison and Hinkley1997, Canty & Ripley Reference Canty and Ripley2016), using the functions boot() and boot.ci(). The R code used to implement the proposed technique is available in Appendix C.Footnote 5
3.1.2 Two or more sound changes
If an alternation Ak requires more than a single sound change, then the historical probability of Ak is estimated as a sum of the historical probabilities of each trajectory Tj that yields the alternation Ak, as shown in (2).
-
(2)

A trajectory Tj denotes a combination of sound changes that yields an alternation Ak. In theory, there are an infinite number of trajectories that yield any given alternation, but for practical purposes, we estimate only the trajectory that involves the least number of sound changes. Historical probabilities of trajectories that require more than three sound changes are assumed to be minor enough to be disregarded for practical purposes.
The historical probability of a trajectory Tj that requires more than a single sound change is estimated from the joint probability of the individual sound changes required for Tj, divided by the factorial of the number of sound changes in trajectory Tj if only one ordering results in the trajectory in question, as shown in (3).
-
(3)

Historical probability is a probability that a language L features an alternation Ak, regardless of the properties of L. In other words, we do not condition historical probabilities on languages that feature a certain property. The historical probability (Pχ) of the first individual sound change S1 is thus estimated from the number of successes (languages with S1) and the number of failures (languages without S1) according to (1), regardless of the phonemic inventories of languages in the sample.
For example, if the target of the first sound change S1 in a trajectory that results in an alternation Ak is a geminate stop, we estimate the historical probability of S1 from the number of languages with the sound change S1 divided by the number of all languages surveyed, including those that do not feature geminate stops. The historical probability of an alternation Ak that requires S1 is simply the probability that the alternation Ak arises in a language L, regardless of whether it features geminate stops.
Once the sound change S1 has operated, however, we know that language L necessarily has the target, result and context of S1. For this reason, we estimate the historical probability of the subsequent sound changes Pχ(S2) by dividing the number of successes (languages with S2) by the number of languages surveyed that feature the target, result and context of S1, if these are also the target of S2. The same is true for any subsequent sound change. Once we condition the probability of sound changes and estimate it from samples of sound changes, given that they have the target, result and context of the previous sound change, we can treat the probabilities of individual sound changes as independent events under the channel bias approach, and estimate Pχ from the product of the probabilities of individual sound changes, as in (4).
-
(4)

To estimate standard errors and BCa confidence intervals for a historical probability of Ak that requires more than a single sound change, the proposed technique samples with replacement from n individual binomial samples (one sample for each individual sound change, constructed as described above) computes the historical probability of each sound change (according to (1)) and then computes the product of the historical probabilities of each individual sound change divided by n!, according to (4). This process returns 10,000 bootstrap replicates of the historical probability of Ak, from which the standard errors and BCa confidence intervals are computed.
3.1.3 Comparison
The proposed technique also allows for the estimation of the difference between the historical probabilities of two alternations, which consequently enables inferential statements on the comparison, as in (5).
-
(5)

The difference between the historical probabilities of two alternations (ΔP χ) is estimated with a stratified non-parametric bootstrap, where Pχ of each individual alternation A1 and A2 is estimated as described in §3.1.1 and §3.1.2 (depending on whether A1 and A2 require trajectories that require one or more sound changes). To compare two historical probabilities, we calculate the difference between Pχ(A1) and Pχ(A2), which returns 10,000 bootstrap replicates, from which the standard errors and BCa confidence intervals are computed.
The proposed technique applied to a difference between two alternations enables a comparison of the two alternations with inferential statements. If the 95% BCa confidence intervals of the difference both fall either below or above 0, then Pχ(A1) and Pχ(A2) are significantly different, with α = 0.05.
3.2 Sample
Samples used for estimating historical probabilities are created from counts of occurrences of sound changes in typological surveys. The proposed technique is most accurate when typological surveys are large, well-balanced and representative. Sound changes in a survey should always be evaluated with respect to the target of the change, its result and its context. Sound-change occurrences in a typological survey should be properly counted: if two or more daughter languages show the result of a sound change that operated at the proto-stage of the two languages, the sound change should be counted as a single event in the proto-language. For a detailed description of how samples for the six alternations in this paper are created, see §4.2, and for lists of languages, see Appendix A.
The most elaborate currently available survey of sound changes used in the paper is the survey of consonantal sound changes in Kümmel (Reference Kümmel2007). One major advantage of Kümmel's survey is that it includes language families with a well-reconstructed prehistory and a well-established subgrouping. This allows for a more accurate coding of the occurrence of a sound change than competing surveys.Footnote 6
Sound changes are counted as single events if they operate at a proto-language stage. While it is sometimes difficult to reconstruct whether a sound change in two related languages operated at the proto-stage or independently in individual branches, especially for typologically frequent sound changes, the survey in Kümmel (Reference Kümmel2007) is the most comprehensive of all available surveys in this respect. Kümmel's subgrouping relies on historical methodology that includes information from phonological as well as morphological and other higher-level evidence.Footnote 7
Kümmel's survey includes approximately 294 languages and dialects of the Indo-European, Semitic and Uralic language families. While it is limited to only three language families, these are families with well-established subgroupings. This allows for proper coding, and at least partially compensates for the lack of representativeness. The results of the analysis can be affected by the fact that many language families are absent from the survey. However, it is likely that such effects are minor, because types of sound changes do not seem to be radically different across different language families (with recurrent sound changes appearing across all families; see Blevins Reference Blevins2007 and §5.3). Additionally, I am unaware of reasons to believe that the representativeness (or bias) of a sample is unequal across different sound changes. Because we are primarily interested in the comparison between historical probabilities of various alternations and less so in their absolute values, the model is less prone to influence from biased samples.
3.3 Assumptions
As with any diachronic model, the proposed technique has to make some simplifying assumptions. In order to estimate the joint probability of two or more sound changes as a product of the historical probabilities of each individual sound change (see (4)), it is assumed that each sound change is an independent event. The proposed model does account for the dependency between sound changes where one sound change alters the target or context of the following sound change. Probabilities of sound changes are estimated on the basis of their targets, results and contexts (§3.2) and, crucially, from samples conditioned on the result of the previous sound change (§3.1.2). Two crucial assumptions of independence remain: that sound change is (i) independent of previous sound changes when the dependence on targets, results and contexts of the previous sound change is controlled for (§3.1.2), and (ii) independent of the global phonemic properties of a language (those properties that do not immediately affect the conditions of sound changes in question).
The first assumption is not controversial when modelling typology within the channel bias approach. The proposed method aims to estimate only the channel bias influences on typology, which is why it has to assume that the probability of sound change is determined only by its frequency of operation, evaluated on a diachronic and unconditioned level.
The second assumption of independence is more problematic: broader phonemic inventories can influence the probabilities of sound changes, especially for vocalic changes (for example due to the effects described in the Theory of Adaptive Dispersion; Liljencrants & Lindblom Reference Liljencrants and Lindblom1972, Lindblom Reference Lindblom, Hardcastle and Marchal1990), but also for consonantal changes. The proposed technique does not model the dependency of sound changes on those phonemic properties that do not immediately affect the targets, results or contexts of the sound changes in question. The sample's representativeness should, however, at least partially cancel out potential dependencies. The sample of sound changes from which the historical probabilities are calculated includes languages with a diverse set of phonemic inventories (see Kümmel Reference Kümmel2007). Additionally, we do not condition estimations of historical probabilities on any specific property of phoneme inventories, which makes the dependency between sound change and more distant phonemic properties less crucial to our proposal. Finally, we are unaware of any properties of phonemic inventories that would affect the rate of the sound changes in question (e.g. intervocalic lenition, occlusion of fricatives, devoicing of stops).Footnote 8
As already mentioned, identification of individual trajectories leading to an alternation Ak is performed manually in the approach described here. While this task is facilitated by the Blurring Process, which describes mechanisms for unnatural processes to arise, it is nevertheless possible that some trajectories that would potentially influence the final result are missing from the estimation. If we assume that the estimated trajectory Tj is indeed the most frequent trajectory leading to Ak and that potential alternative trajectories do not crucially influence the overall historical probability of an alternation, we can generalise the historical probability of that particular trajectory to the historical probability of the alternation. If such an assumption is not met, however, then the proposed technique estimates only the probability that an alternation Ak arises from a trajectory Tj.Footnote 9 This paper assumes that the estimated trajectories are the most frequent, and that potential alternative trajectories do not crucially influence the results.
The proposed model aims to estimate the channel bias influences on typology. It is possible that learnability influences the probabilities of individual sound changes: learnability can increase or decrease the likelihood of a phonetic precursor being phonologised (as argued by Moreton Reference Moreton2008; for criticism, see Kapatsinski Reference Kapatsinski2011 and Yu Reference Yu2011). Even if the probabilities of individual sound changes are crucially influenced by learnability (and therefore by analytic bias), and even if learnability causes a higher rate of occurrence of certain sound changes in combination, the requirement that more than one sound change needs to operate in a language for unmotivated alternations and unnatural alternations to arise has to be independent of learnability. This means that at least a portion of the estimated probabilities needs to be influenced by the channel bias.
What is not accounted for in the model is the functional load of individual phonemes (Wedel Reference Wedel2012, Wedel et al. Reference Wedel, Kaplan and Jackson2013, Hay et al. Reference Hay, Pierrehumbert, Walker and LaShell2015), as well as other factors that could potentially influence probabilities of sound changes, such as lexical diffusion or lexical/morpheme frequency during the initial stages of sound change (Bybee Reference Bybee2002), language contact and sociolinguistic factors. The model makes no assumptions about how sound change is initiated or spread. These factors can mostly be disregarded, because the goal is to estimate the historical probability of alternation Ak operating in a language L with no conditional properties.
Finally, the proposed technique does not directly model the temporal dimension. In the absence of temporal information, we have to make some simplifying assumptions. These are not unique to the present proposal, and are to some extent desirable. The technique estimates historical probabilities within a timeframe that approximates the average timeframe of the languages in the sample. The model also assumes that in order for a resulting alternation to be productive, all sound changes need to operate within one language. While this might be too restrictive, it is desirable to limit the timeframe in which sound changes and corresponding processes have to operate productively for the resulting alternation to be productive. For example, the combination of sound changes (the Blurring Process) that would result in postnasal devoicing in Yaghnobi operates over three languages, and fails to result in a productive synchronic alternation (Beguš Reference Beguš2019). The model also assumes that once a sound change has occurred in a language, it can reoccur. This is a closer approximation to reality than to assume that a sound change cannot operate in daughter languages once it has already operated in the parent language.
The historical probability of an unnatural alternation depends not only on sound changes that are required for the alternation to arise, but also on the probability that the sound change with the opposite effect (in this case, the natural sound change) will operate on the unnatural system and destroy the evidence for it. Influences of potential natural sound changes are not modelled, because the historical probabilities of the natural sound changes are relatively similar for the processes estimated in this paper, and we do not expect this additional factor to alter the results significantly.Footnote 10 For other processes not estimated in this paper, the inclusion of the probability of the natural sound change in the model might alter the outcomes significantly.
4 Applications
4.1 Trajectories
The three natural alternations have obvious origins – three single natural sound changes: postnasal voicing, intervocalic voicing and final devoicing. For the unnatural alternations, we first identify sound changes in the Blurring Process (see §2) that yield the alternation in question. If A > B / X is a natural sound change, then B > A / X is unnatural. Tables Ia–c represent schematically how the unnatural B > A / X arises via the Blurring Process (see §2; Beguš Reference Beguš2018, Reference Beguš2019, Beguš & Nazarov Reference Beguš and Nazarov2018), together with the actual sound changes that yield the unnatural alternation. A combination of the following three natural and well-motivated sound changes yields postnasal devoicing in all known cases: the fricativisation of voiced stops in non-postnasal position, the unconditioned devoicing of voiced stops and the occlusion of voiced fricatives to stops (Table Ia).Footnote 11
Table I Blurring Processes yielding (a) postnasal devoicing, (b) intervocalic devoicing, (c) final voicing.
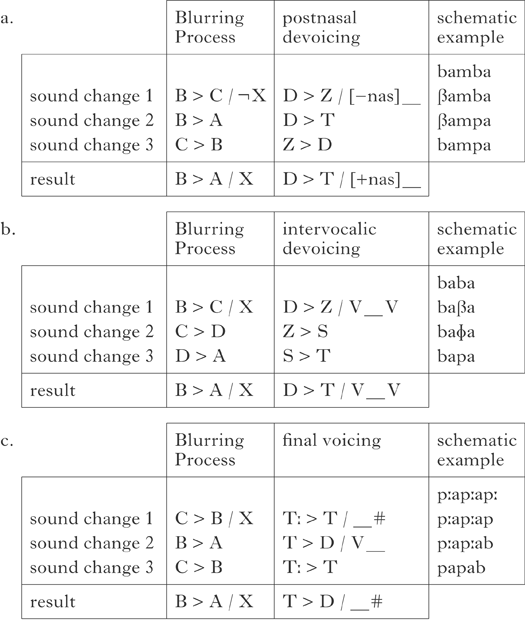
Beguš (Reference Beguš2018) argues that intervocalic devoicing results from three sound changes. Voiced stops fricativise intervocalically, voiced fricatives devoice and voiceless fricatives are occluded to stops (see Table Ib). The result is the unnatural intervocalic devoicing (D > T / V_V).
Final voicing is arguably unattested either as a synchronic alternation or as a sound change (Kiparsky Reference Kiparsky2006, Lipp Reference Lipp2016, Beguš Reference Beguš2018; for an opposing view, see Yu Reference Yu2004, Rood Reference Rood, Rudin and Gordon2016).Footnote 12 A number of diachronic scenarios exist, however, that would yield final voicing; these are identified in Kiparsky (Reference Kiparsky2006). Most of the scenarios either include more than three sound changes or do not result in a phonological alternation, but in a static phonotactic restriction (§4.2). One possible scenario that involves three sound changes and that would result in final voicing is Kiparsky's Scenario 1, which is used here for estimating the historical probability of final voicing.Footnote 13 For the sound changes in Scenario 1 to result in synchronic alternations, we need to assume that geminate simplification first operated word-finally, and only later targeted other geminates. Without this assumption, the sound changes in Scenario 1 would result in a phonotactic restriction. The three sound changes operating to yield final voicing in this scenario are geminate simplification in word-final position, voicing of postvocalic non-geminate stops and unconditioned geminate simplification (see Table Ic).
4.2 Counts
Samples of sound changes on the basis of which the estimations of historical probabilities are performed were constructed from counts of occurrences and languages surveyed (from Kümmel's Reference Kümmel2007 database). The count of sound-change occurrences was derived from the number of languages listed by Kümmel for each sound change. To avoid counting a single sound change that operates at a proto-stage and is reflected in several daughter languages as independent events, sound changes with exactly same outcome in closely related languages were counted as single events (as grouped together by Kümmel Reference Kümmel2007). While it is possible that some dependencies still exist in the data, it is difficult to estimate their number. We assume that potential dependencies do not crucially affect the results.
If a sound change is reported to target a subset of the three major places of articulation (labial, dorsal, velar), rather than the entire set, the counts for alternations that require more than one sound change were multiplied by a coefficient that proportionally penalises the counts. For example, counts of sound changes that target only two places of articulation are multiplied by two-thirds in order to reduce the possibility of final estimated probabilities being inflated: if the first sound change targets two places of articulation and the second sound change targets the third place of articulation, such a combination would not result in an unnatural process.
Postnasal voicing as a sound change is reported in approximately 28 languages by Kümmel, and intervocalic voicing (including postvocalic voicing) in approximately 38. Final devoicing is reported in approximately 24 languages (summarised in Table II). For raw counts, see Appendix A: §1–§3. Postnasal voicing, intervocalic voicing and final devoicing that target a single series of stops are counted without penalisation, together with cases in which these sound changes target more than a single place of articulation.
Table II Counts of sound changes in Kümmel (2007) for natural alternations.

The first sound change in the Blurring Process that results in postnasal devoicing, the fricativisation of voiced stops, is reported in approximately 66 languages. In 32 languages, the sound change is reported to target all three major places of articulation, in eleven languages the sound change targets two places of articulation and in 23 languages one place of articulation. The final count is thus ≈47 (32 + 11 × ⅔ + 23 × ⅓). Instances of intervocalic and postvocalic fricativisation are included in the count (not only cases with fricativisation in all but postnasal position), because the result of such fricativisation after the other two sound changes would also be a system analysed as postnasal devoicing.Footnote 14 The probability of the first of the sound changes in the Blurring Process that results in postnasal devoicing is estimated on the basis of number of successes (languages in the survey with that sound change) and the total number of languages surveyed (294), without conditioning on the sample. The sample for estimating the probability of the first sound change is unconditioned because the historical probability of Ak is the probability of Ak arising in a language, regardless of the properties of its phonemic inventory (see §3.1.2). Once the first sound change has operated, however, we know that the language in question needs to have voiced stops in its inventory. The historical probability of the second sound change, which targets voiced stops, is therefore estimated from the number of successes (languages in the survey with that sound change) and the number of languages with voiced stops. The second change (D > T) is found in ≈15 (13 + 1 × ⅔ + 3 × ⅓) languages (including cases of devoicing that are the result of chain shifts). Approximately 31 languages lack voiced stops in Kümmel's survey, meaning that Pχ is estimated on the basis of 294 ― 31 = 263 languages surveyed.Footnote 15 After the two sound changes operate, we also know that the language L has voiced fricatives. The historical probability of the last sound change is estimated on the basis of the number of languages with occlusion of voiced fricatives and the number of languages with voiced fricatives (allophonic or phonemic). Approximately 216 languages have voiced (bi)labial, alveolar/dental or velar non-strident fricatives (including the labiodental voiced fricative /v/), according to Kümmel. In ≈17 (1 + 5 × ⅔ + 38 × ⅓) languages, occlusion of fricatives is reported as a sound change. The counts for intervocalic devoicing are performed in the same manner as the counts for postnasal devoicing, and are given in Table III.
Table III Counts of sound changes in Kümmel (2007) for unnatural alternations.

The historical probability of final voicing is estimated on the basis of the one scenario in Kiparsky (Reference Kiparsky2006) that would result in an alternation involving final voicing. Scenarios that would lead to final voicing as a static phonotactic restriction and could involve fewer than three sound changes are excluded. There are three main reasons for distinguishing alternations from static phonotactic restrictions in a diachronic model (Beguš Reference Beguš2019), despite the two phenomena likely being part of the same synchronic grammatical mechanisms (Prince & Smolensky Reference Prince and Smolensky1993, Hayes Reference Hayes, Kager, Pater and Zonneveld2004, Pater & Tessier Reference Pater, Tessier, Slabakova, Montrul and Prévost2006). First, unnatural phonotactic restrictions provide considerably less reliable evidence for learners, because the evidence is distributional, rather than appearing within the same morphological unit. This means that it is more likely that a phonotactic process will not be acquired by the learners. Second, alternative analyses of data are often available in the case of phonotactic restrictions, but not for alternations, where evidence for a process comes from within the same morphological unit. Finally, typological surveys of phonotactic restrictions are considerably more difficult to carry out than typological surveys of alternations. In the absence of typological studies, it is difficult to evaluate the predictions that the channel bias model makes for phonotactic restrictions. In fact, final voicing as a phonotactic restriction might not be as rare as has been suggested, with at least two potential phonological systems attested in which voiceless stops do not surface word-finally, but voiced stops do (for example in Ho and some dialects of Spanish; see Beguš Reference Beguš2019).Footnote 16
Counts of the sound changes that lead to final voicing as an alternation are as follows. In three languages, word-final geminates are reported to simplify to singleton stops. (This sound change is necessary if we want the scenario to result in an unnatural alternation, rather than a static phonotactic restriction.) Because this is the first in the series of changes and we do not condition Pχ on any property of the language, as before, the historical probability is estimated from the total number of languages surveyed. The second sound change, postvocalic voicing of voiceless stops, is reported in approximately 23 languages (corrected for place of articulation). The intervocalic condition is excluded from the count, as voicing of intervocalic stops would not target final stops. Because all 294 languages surveyed have voiceless stops, they are all included in the count for estimating the historical probability of the second sound change.Footnote 17 Finally, simplification of geminates is reported in 21 languages. It is difficult to estimate how many languages in Kümmel (Reference Kümmel2007) allow geminate voiceless stops. While few languages have phonologically contrastive geminates, many more allow sequences of two identical stops at morpheme boundaries (so-called fake geminates; Oh & Redford Reference Oh and Redford2012). To estimate the number of languages that allow such sequences, Greenberg's (Reference Greenberg1965) survey of consonantal clusters and Ryan's (Reference Ryan2019) survey of phonemic geminates were used. At least 30% of languages in Greenberg's survey of approximately 100 languages allow stop–stop final clusters. The number of languages in our sample that allow homorganic stop–stop sequences can be approximated from the proportion of languages that allow phonemic geminates and from the proportion that allow sequences of stops. Languages that allow clusters of stops at morpheme boundaries should in principle allow clusters of homorganic stops: if geminate clusters were simplified, the sound change of simplification would be reported in our sample. The number is thus estimated at 88 (30% of 294 languages). That this estimate is accurate is suggested by a survey of phonemic geminates: Ryan Reference Ryan2019 estimates that approximately 35% of 55 genealogically diverse languages surveyed have phonemic geminates.
5 Results
5.1 Individual alternations
Table IV shows the Historical Probabilities with estimated 95% BCa confidence intervals for the six natural and unnatural alternations discussed above. Figure 1 shows the distributions of bootstrap replicates for the historical probabilities (Pχ) of these alternations. The results show a substantial difference between the historical probabilities of the natural and unnatural groups. The model thus predicts that the unnatural alternations will be substantially less frequent than their natural counterparts.
Table IV Estimated Pχ (in %) for natural and unnatural alternations with 95% BCa confidence intervals. We also compute profile CIs from an empty logistic regression, for comparison. The largest difference between the confidence intervals is 0.5%, which suggests that the proposed model estimates CIs with a high degree of accuracy.


Figure 1 Bootstrap replicates for natural and unnatural alternations. The plots show the observed Pχ (solid line) and the 95% BCa confidence intervals (CIs) (dashed line) for natural alternations (PNV = postnasal voicing, PND = postnasal devoicing, IVV = intervocalic voicing, IVD = intervocalic devoicing, FD = final devoicing, FV = final voicing). The vast majority of bootstrap replicates for unnatural alternations fall outside the limits of the plot.
5.2 Comparison of alternations
One of the advantages of the proposed model is that inferential statistics can be performed on the comparison between the historical probabilities of any two alternations. Significance testing is performed by estimating a difference between the historical probabilities of two alternations (see §3.1.3).
The historical probabilities of all three natural alternations in Fig. 1 are significantly higher than those of their unnatural counterparts. Table V includes estimates and 95% BCa confidence intervals of the difference in historical probabilities (ΔPχ) for each natural–unnatural alternation pair.
Table V Estimated ΔPχ (in %) for natural–unnatural alternation pairs with 95% BCa confidence intervals. * indicates significant differences.

We can also compare alternations within the unnatural group. Figure 2 shows bootstrap replicates of the individual historical probabilities of the three unnatural alternations. The figure shows that the historical probability of postnasal devoicing is higher than those of the other two unnatural alternations. By estimating the difference between two alternations, we can test, for example, whether Pχ(PND) and Pχ(IVD) or Pχ(PND) and Pχ(FV) are significantly different, as shown in (6).
-
(6)


Figure 2 Bootstrap replicates unnatural alternations. The plots show the observed Pχ (circle, triangle and square) and the 95% BCa CI (solid lines).
Because the 95% BCa CIs of the difference in historical probability between postnasal devoicing and final voicing and between postnasal devoicing and intervocalic devoicing lie above zero, it can be concluded that the historical probability of postnasal devoicing (Pχ(PND)) is significantly higher than the historical probabilities of final voicing (Pχ(FV)) and intervocalic devoicing (Pχ(IVD)) (with α = 0.05).
The proposed technique makes some simplifying assumptions that introduce confounds to the estimation of historical probabilities (see §3.2, §3.3 and §4). Because differences in the historical probabilities among unnatural alternations are considerably smaller than differences between natural and unnatural pairs (Fig. 1), estimation of these differences is substantially more likely to be influenced by these confounds, and therefore to be less reliable. Until more comprehensive surveys are available, however, the proposed model makes, as far as I know, the most accurate approximations of historical probabilities of alternations, both for natural–unnatural alternation pairs and for alternations within the unnatural group.
5.3 Comparing historical probabilities with observed synchronic typology
We can evaluate the model's predictions by comparing historical probabilities with independently observed typology of synchronic alternations.Footnote 18 Table VI compares historical and observed synchronic probabilities. Historical probabilities are estimated as described above (see §4 and Table IV). The synchronic typology is estimated with a non-parametric bootstrap technique, in the same way as described in §3.1.1, except that the estimation is based on the numbers of languages in a sample with and without a particular synchronic alternation. The database used for estimating synchronic typology is PBase (Mielke Reference Mielke2019), which surveys 629 languages in total. Postnasal voicing is attested in 28 languages, intervocalic voicing in 51 and final devoicing in 31 (the languages on the basis of which the count was performed are listed in Appendix B). All three alternations were counted, even if they target only one place of articulation. Neither the historical (Kümmel Reference Kümmel2007) nor the synchronic sample was constructed specifically for the purpose of establishing typology of processes that target feature [voice], making them less prone to biases.
Table VI A comparison of historical probabilities (Pχ) and observed synchronic typology with 95% BCa CIs for natural and unnatural processes.

The estimations of the synchronic typology of unnatural alternations can be computed (as in Table VI) from the surveys of unnatural processes in Beguš (Reference Beguš2018, Reference Beguš2019) and Beguš & Nazarov (Reference Beguš and Nazarov2018). Postnasal devoicing has been confirmed as a fully productive synchronic alternation in two related languages (Tswana and Shekgalagari) and as a morphophonological alternation in a number of others (e.g. Buginese and Nasioi; see Beguš Reference Beguš2019). For the purpose of comparison, only fully productive alternations were counted in the synchronic typology. Because Tswana and Shekgalagari are closely related, postnasal devoicing here was counted as a single occurrence. Intervocalic devoicing is attested only once as a morphologically conditioned synchronic process (Bloyd Reference Bloyd2015), although detailed descriptions are lacking. To the best of my knowledge, final voicing is not attested as a productive phonological alternation in any language, which is why its synchronic typological probability is estimated as less than P = 1/600 (an approximate estimate of languages surveyed in these surveys of unnatural alternations is 600).Footnote 19
Table VI and the corresponding plot of estimated historical and synchronic probabilities with 95% BCa CIs in Fig. 3 suggest that the model correctly predicts natural alternations to be considerably more frequent than their unnatural alternations. Historical probabilities and observed synchronic typology also match to the extent that the 95% BCa confidence intervals of both historical and synchronic typological probabilities overlap for the compared processes. It needs to be stressed here that, for unnatural processes, historical probabilities and observed synchronic typology are completely independent. In other words, the model estimates the probability of a combination of three sound changes, none of which is individually related to the unnatural synchronic alternation from which synchronic typological probabilities are estimated.

Figure 3 Observed historical (H; solid line) and synchronic (S; dashed line) probabilities (in %) with 95% BCa CIs from Table VI.
6 Implications
The technique employed here also helps in the identification of mismatches in predictions between the analytic bias and channel bias approaches to typology. If two typologically different alternations show no learnability differences, but have significantly different historical probabilities, it is reasonable to assume that the differences in the observed typology between the two alternations is influenced by the channel bias factor. On the other hand, if two typologically different alternations have the same historical probabilities and show differences in learnability, it is reasonable to assume that these differences result from the analytic bias factor.
The proposed model suggests that the observed rarity of unnatural alternations targeting feature [voice] is primarily influenced by the channel bias factor. The typology is predicted with relatively high accuracy (§5.3 and Fig. 3), whereas learning experiments found no differences between the natural and unnatural alternations for any of the three pairs (Seidl et al. Reference Seidl, Buckley and Cristià2007, Do et al. Reference Do, Zsiga and Havenhill2016, Glewwe Reference Glewwe2017, Glewwe et al. Reference Glewwe, Zymet, Adams, Jacobson, Yates, Zeng and Daland2018).
The model predicts not only that unnatural alternations will be rare (§4), but also that complex alternations will be less frequent than simple alternations. The minimality principle (cf. §2), which is at least a strong tendency, states that sound change is a change in one feature (or the deletion or reordering of feature matrices) in a given environment. This means that featurally complex alternations that change more than a single feature can only arise from the phonologisation of more than one sound change. Because the probability of a combination of two sound changes will be lower than the probability of one sound change, all else being equal, featurally complex alternations are predicted to be typologically less frequent within the channel bias approach. Exactly the same generalisation is, however, also predicted by the analytic bias approach to typology: numerous studies have confirmed that featurally complex alternations are consistently underlearned compared to featurally simple alternations (complexity bias; Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb).
There is a crucial mismatch between the predictions of the analytic bias and channel bias approaches with respect to unnatural alternations. The channel bias approach predicts that the more sound changes an alternation requires, the lower the historical probability of that alternation, regardless of its complexity (see Table VII). In other words, the prediction that complex alternations will be rare is violable: if the three sound changes of a Blurring Process result in a simple unnatural alternation, it will still be predicted that the simpler alternation will be less frequent than an unmotivated complex alternation, because the first requires three sound changes to arise and the latter only two (§2).
Table VII Mismatches in predictions (framed) between the channel bias approach (Pχ) and the complexity bias approach (Pcomplex) for postnasal devoicing. The sound-change column represents the three sound changes from which the unnatural process postnasal devoicing results, and the alternation column represents the synchronic alternation after each of the three sound changes. The Pχ column gives the estimated probability of each alternation with 95% BCa lower and upper 95% CIs. The features (F) column gives the number of features a learner has to learn for each synchronic alternation.

We can estimate the historical probabilities for each step in the Blurring Process that leads to unnatural alternations. Take as an example postnasal devoicing. The historical probabilities of each resulting alternation (after the first, second and third sound changes) were estimated as described in §3.Footnote 20 The Pχ columns in Table VII illustrate that each additional sound change decreases the historical probability of the resulting alternation.
On the other hand, the analytic bias approach predicts that structurally more complex alternations will be typologically less frequent because they are more difficult to learn than structurally simple alternations (complexity bias has been confirmed in many studies, almost without exception; e.g. Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb). While many criteria for complexity in phonological alternations can be invoked, I focus on the measure of complexity in Moreton et al. (Reference Moreton, Pater and Pertsova2017), which accounts for learnability asymmetries in several earlier studies (for an overview, see Moreton & Pater Reference Moreton and Pater2012a, Reference Moreton and Paterb), and is based on ‘concept learning’. The complexity of an alternation is derived primarily from the number of features manipulated by an alternation.
If we analyse each step in the Blurring Process in terms of such synchronic complexity, the first two sound changes indeed increase the complexity of the resulting alternation, but the third change decreases its complexity.Footnote 21 The alternation Z → T / [+nas] _ manipulates two feature values, [±continuant] and [±voice], while D → T / [+nas] _ (postnasal devoicing) manipulates only [±voice]. From a phonological perspective, the first is more complex than the latter (Moreton et al. Reference Moreton, Pater and Pertsova2017).
Complexity bias thus predicts that the alternations that arise from the first and second sound changes in the Blurring Process will be increasingly rare, but predicts that the structurally simpler alternations resulting from the combination of all three sound changes will be more frequent than the complex alternation requiring only two sound changes.
The mismatched predictions illustrated in Table VII provide new information for disambiguating analytic bias and channel biases. The analytic bias–channel bias complexity mismatch can be directly evaluated against the observed typology: if unmotivated structurally complex alternations that require two sound changes are typologically more common than structurally simpler unnatural alternations, channel bias has to be the leading cause of this particular typological observation. If, on the other hand, structurally more complex unmotivated alternations that require two sound changes are typologically less frequent than what would be predicted by the channel bias approach, we have a strong case in favour of the analytic bias influence, and more precisely in favour of complexity bias within the analytic bias approach to typology.
In fact, typological observations suggest that the complex synchronic alternation Z → T / [+nas] _ that results from the first two sound changes in a Blurring Process might be attested less frequently than would be predicted by channel bias, suggesting that complexity bias influences this distribution. The historical probability of Z → T / [+nas] _ is significantly higher than the historical probability of postnasal devoicing. The difference is estimated at ΔPχ(Z → T / [+nas] _) = 0.4%, [0.2%, 0.8%]. In other words, the historical probability of the alternation Z → T / [+nas] _ arising through two sound changes is predicted to be approximately fifty times as frequent as the historical probability of postnasal devoicing (see Table VII). Surface synchronic typology, however, does not conform to this generalisation.
A system in which postnasal devoiced stops contrast with voiced fricatives elsewhere (a complex alternation that arises via the combination of two sound changes) is synchronically confirmed in Konyagi, Punu, Pedi, Sie and potentially Nasioi (Dickens Reference Dickens1984, Santos Reference Santos1996, Hyman Reference Hyman, Hume and Johnson2001, Merrill Reference Merrill2014, Reference Merrill2016a, b, Brown Reference Brown2017).Footnote 22 Other languages are more difficult to classify, because some of them appear to feature full postnasal devoicing only for a subset of places of articulation. While Z → T / [+nas] _ indeed appears to be more frequent than postnasal devoicing, the magnitude of the difference is smaller than predicted by the channel bias.
Even more intriguing is the high frequency at which the third sound change in the Blurring Process, the occlusion of voiced fricatives to stops (Z > D), operates on synchronic systems that feature the alternation Z → T / [+nas] _ (after the first two changes). The historical probability of the third sound change that leads to postnasal devoicing, occlusion of voiced fricatives for languages that have voiced fricatives in the system, estimated independently of the Blurring Process (i.e. estimated from an unconditioned diachronic sample), is Pχ(Z > D) = 20.4% [14.8%, 25.5%]. Of the languages in the survey in Beguš (Reference Beguš2019) that undergo the first two sound changes in the Blurring Process, which leads to postnasal devoicing, six (out of ten) feature occlusion of stops for at least one place of articulation or in at least one position in the word.Footnote 23 If we take only cases in which the occlusion of fricatives targets more than two places of articulation, only Tswana, Shekgalagari, Makuwa and Murik would count. It does appear, however, that the occlusion of voiced fricatives in a synchronic system that undergoes the first two sound changes is more frequent than the model predicts for the occlusion of voiced fricatives in general.
To test the hypothesis that the last sound change operates with higher frequency than would be predicted by only the channel bias approach, we can compare the unconditioned historical probability of the occlusion of fricatives with the historical probability of the occlusion of fricatives in those languages that have already undergone the first two sound changes in the Blurring Process that lead to postnasal devoicing. In other words, we compare the probability of the occlusion of fricatives regardless of whether it simplifies the alternation (assuming only channel bias influences) with the probability of the occlusion of fricatives operating in the Blurring Process, where it simplifies the alternation and consequently its learnability. Counts for the unconditioned historical probability of the occlusion of fricatives are based on the survey of sound changes in Kümmel (Reference Kümmel2007). 44 languages with voiced fricatives (out of 216 surveyed) undergo the occlusion of voiced fricatives. As already mentioned, under the less conservative count, six out of ten languages with occlusion and fricative devoicing show occlusion for at least one place of articulation or for at least one context (word-initially in Nasioi).Footnote 24 The difference between the two counts is statistically significant (p = 0.009; Fisher's Exact Test). This means that the last sound change in the Blurring Process that decreases the complexity of the resulting alternation operates at significantly higher rates than would be predicted if we assumed only channel bias influences.Footnote 25
This suggests that the high rate of occurrence of the third sound change in the Blurring Process (in the case of postnasal devoicing, the occlusion of fricatives) is likely an influence of complexity bias within the analytic bias approach. While analytic bias probably does not crucially influence the probabilities of the first two sound changes in the Blurring Process in the direction that interests us, because they increase complexity and therefore would be predicted to reduce learnability, it is likely that the frequency of the third sound change, and therefore the lower probability of the more complex unmotivated alternation, is influenced precisely by complexity bias.Footnote 26 This paper has identified and described one such instance; investigation of further such cases should yield a better understanding on how learnability and sound-change frequency interact.
7 Conclusion
This paper has proposed a technique for estimating channel bias influences on phonological typology using the statistical technique of bootstrapping. Historical probabilities of alternations were estimated on the basis of two diachronic factors: the number of sound changes required for an alternation to arise and their respective probabilities.
The model was applied to six natural and unnatural alternations targeting the feature [voice]. It can (i) estimate the historical probability of any synchronic alternation, both attested and unattested, (ii) compare the historical probabilities of two alternations and perform inferential tests on the comparison and (iii) compare the historical probabilities to independently observed synchronic typology, in order to evaluate the channel bias influences on typology. Finally, we identified mismatches in predictions between the analytic bias and channel bias approaches, which yields new insights into the discussion of different influences on phonological typology. The results suggest that the typological difference between natural and unnatural alternations targeting the feature [voice] is primarily due to channel bias, but that the relatively low frequency of complex alternations and the higher rate of operation of sound changes that simplify an alternation are due to analytic bias.
These conclusions have direct theoretical implications. Synchronic grammar should ideally derive all observed patterns, and at the same time exclude impossible processes. Typological observations often prompt adjustments in grammar design. The proposed framework suggests that some typological gaps are historical accidents that need not be encoded in synchronic grammars, and quantifies these gaps. On the other hand, this paper has also suggested that some typological observations, such as the avoidance of complex alternations, cannot be explained only within the channel bias approach, and that these preferences should indeed be encoded in synchronic grammar. The paper limits the application of the technique to six alternations targeting feature [voice]. Estimation of channel bias and analytic bias influences should be performed on further alternations, in order to gain a better understanding of which observations result from constraints in synchronic grammar and which from diachronic development.















