Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T15:50:05.613Z Has data issue: false hasContentIssue false
  • English
  • Français

Coalescence as autosegmental spreading and delinking

Published online by Cambridge University Press:  01 March 2021

Joanna Zaleska Open the ORCID record for Joanna Zaleska [Opens in a new window]
Joanna Zaleska*
Affiliation:
Humboldt-Universität zu Berlin
*
*E-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Phonological coalescence, understood as a type of synchronic alternation in which two phonological elements seem to fuse into one, presents a prima facie challenge for versions of Optimality Theory that assume the principle of containment. If all underlying material has to be present in the output form, replacing two input elements with a single output element is not straightforward. I argue that, under the assumptions of Autosegmental Coloured Containment Theory, a distinct operation of coalescence is unnecessary, as all major types of coalescence patterns can be analysed in terms of (i) adding new association lines between some autosegmental nodes, and (ii) the underparsing of other nodes, leading to their phonetic non-realisation. The proposed analysis accurately reflects the heterogeneity of coalescence alternations, which are shown to fall into three different types.

Type
Articles
Information
Phonology , Volume 37 , Issue 4 , November 2020 , pp. 697 - 735
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

1 Introduction

For over two decades, the mainstream framework for phonological description and analysis has been Optimality Theory (OT; Prince & Smolensky Reference Prince and Smolensky1993), a model in which a set of surface candidates for a given input form is evaluated against a language-specific hierarchy of universal constraints. These include markedness constraints, which penalise certain structures, and faithfulness constraints, which require identity between the input and the output. A substantial body of research in Optimality Theory further assumes that faithfulness is mediated by a relation of correspondence between elements of the input and the output (McCarthy & Prince Reference McCarthy and Prince1994, Reference McCarthy, Prince, Beckman, Dickey and Urbanczyk1995). This approach allows for considerable freedom in how far an output candidate can in principle diverge from the input. Elements at both levels of representation are permitted to have multiple correspondents (manifested as coalescence or fission) or no correspondents at all (interpreted as deletion or epenthesis).

On an alternative interpretation of faithfulness, first put forward by Prince & Smolensky (Reference Prince and Smolensky1993), the input is treated as a substructure of the output. Underlying material that seems to have undergone deletion is never literally removed, but is ignored by the phonetic component, and hence remains unpronounced. Consequently, faithfulness constraints do not have to compare the input and the output, but can instead assess output structures. While the first implementation of this idea, Prince & Smolensky's Parse/Fill model, was rejected in favour of Correspondence Theory because of the former's unsatisfactory treatment of epenthesis and incorrect predictions in the area of reduplication, Coloured Containment Theory, an alternative approach developed by van Oostendorp (Reference Oostendorp2006, Reference Oostendorp2007) is argued not only to be free from the shortcomings of its predecessor, but also to have a number of advantages over Correspondence Theory. It has been shown that the assumption of covert output structures can be successfully employed to account for a wide array of data that pose a challenge to standard OT, including incomplete neutralisation (van Oostendorp Reference Oostendorp2008), phonological opacity (Trommer Reference Trommer2011), chain shifts (Popp Reference Popp2019) and grandfather effects (Trommer Reference Trommer2015), as well as additive and subtractive morphological length manipulation (Zimmermann Reference Zimmermann2017).

In spite of its appeal, Coloured Containment Theory has a potential drawback: it does not seem to offer a straightforward way to deal with phonological coalescence. In this framework, the restricted set of basic operations available to Gen does not include a direct equivalent of the two-to-one mapping possible in Correspondence Theory. Since candidate output forms are generated exclusively by delinking underlying association lines and/or adding new associations and autosegmental nodes to the input form, a hypothetical operation turning two input segments into one would be difficult to implement without considerable complication of the representational or algorithmic assumptions.

In this article, I argue that a distinct operation of coalescence is unnecessary if the assumptions of Autosegmental Coloured Containment Theory (Trommer Reference Trommer2011, Reference Trommer2014, Trommer & Zimmermann Reference Trommer and Zimmermann2014) are adopted. I offer an account of coalescence alternations that decomposes coalescence into independently motivated subcomponents: (i) the addition of association lines between underlyingly unassociated autosegmental nodes, and (ii) the underparsing of autosegmental nodes (and their ensuing non-realisation), resulting from delinking or non-prosodification, as in (1). As a starting point, I assume a classification of coalescence patterns into two broad types on the basis of their effect on the length of the affected string. In reductive coalescence, the number of underlying segments is reduced on the surface; in non-reductive coalescence, it remains the same, but the resulting structure is treated as a single unit for the purposes of other phonological processes. In the analysis proposed in this paper, the distinction is reflected in the position of the node that undergoes spreading: the daughter of an underparsed node in reductive coalescence, (1a), and its sister in non-reductive coalescence, (1b).Footnote 1

  1. (1)

In addition, I discuss arguments in favour of viewing reductive coalescence as encompassing two types of alternations: assimilatory coalescence, in which the apparent fusion of two segments results from the interaction of independently motivated processes of assimilation and spreading, and compensatory coalescence, which cannot be decomposed in this way. This distinction is captured by using different constraints as the drivers of the spreading subcomponent: Max[F] faithfulness, requiring the phonetic realisation of specific input features in compensatory coalescence, and general clones of markedness constraints, which assess both the overt and covert parts of an output candidate, in assimilatory coalescence.

The remainder of this article is structured as follows. §2 outlines the range of phenomena that have been viewed as coalescence in the literature, and motivates the three-way classification of coalescence patterns. §3 presents the basic principles and assumptions of Autosegmental Coloured Containment Theory, and develops a containment-based account of representative examples of coalescence. §4 compares the proposed approach to coalescence with alternative accounts, with a particular focus on Correspondence Theory and autosegmental phonology. §5 concludes.

2 Coalescence as a phenomenon

In the linguistic literature, the terms coalescence, contraction and fusion have been used to describe synchronic alternations where two phonological elements are replaced by a single one, as well as operations and transformations that lead to such alternations. In this section, I focus on the former use, and present the range of phenomena that have been subsumed under these terms. I classify coalescence alternations into two broad types, reductive and non-reductive, the former further subdivided into assimilatory and compensatory coalescence.

2.1 Reductive coalescence

A prototypical example of reductive coalescence involves an alternation in which a sequence of two adjacent underlying segments surfaces as a single output segment which has some properties of each of the input sources. This is most commonly seen in hiatus resolution. In languages such as Xhosa and Chumburung in (2), a sequence of vowels of different quality is simplified to a single vowel, which has the backness of one of the inputs, but the height or ATR specification of the other. In Xhosa, coalescence applies to resolve vowel hiatus across various morpheme boundaries, for example between the possessive marker /ɓa-/ and the vocalic class prefix of a noun it attaches to, or between a noun and the locative suffix /-ini/ (all Xhosa data in the paper are from Pahl et al. Reference Pahl, Pienaar and Ndungane1989, Mini & Tshabe Reference Mini and Tshabe2003 or Tshabe & Shoba Reference Tshabe and Shoba2006). Input /a-i/ and /a-u/ sequences formed across these boundaries are realised as output [e] and [o] respectively. Thus the resulting mid vowels are [―high], like the input /a/, but their values for [back] and [round] correspond to the second vowel in the input sequence. In Chumburung, where hiatus resolution affects vowel sequences spanning word boundaries, the resulting vowel has the [low], [back] and [round] specification of the second vowel in the underlying sequence, but may have the [ATR] and [high] values of the first one (all Chumburung data are from Snider (Reference Snider1989, Reference Snider2018) or from Keith Snider (personal communication)).Footnote 2

  1. (2)

While reductive coalescence is often discussed in the context of hiatus resolution, it can also affect consonant clusters and combinations of vowels and consonants. The latter can be observed in Chumburung. When the first vowel in an underlying sequence is rounded, it fuses with the preceding consonant, yielding a labialised segment, as in /átɔ́ àsá/ → [àtʷàsá] ‘three things’ (Snider Reference Snider2018: 103).

A classic example of coalescence affecting sequences of consonants is ‘nasal substitution’ in Indonesian (De Guzman Reference De Guzman1978, Pater Reference Pater, Kager, van der Hulst and Zonneveld1999, Reference Pater and Lombardi2001, Blust Reference Blust2004), where the final velar nasal in the active voice prefix /məŋ-/ seems to fuse with a stem-initial voiceless stop or fricative, creating a nasal with the place of articulation of the input obstruent, as in (3) (Lapoliwa Reference Lapoliwa1981: 106–107, Sneddon et al. Reference Sneddon, Adelaar, Djenar and Ewing2010).

  1. (3)

A less prototypical type of reductive coalescence includes non-local patterns, such as the one described for Chaha (Banksira Reference Banksira2013), where the exponent of the impersonal subject suffix, realised as [w] when it occurs between vowels, as in (4a), fuses with the nearest preceding labial or velar segment when it is underlyingly preceded by a consonant, skipping intervening vowels and coronal consonants, as in (b).

  1. (4)

Finally, reductive coalescence includes alternations in which the number of segments is reduced without loss of featural content, as could be argued for Polish, where a stem-final dental stop (e.g. in [studɛnt] ‘student’) and an alveolar fricative of the denominal adjectivising suffix /-sk/ (e.g. [xwɔp-skʲ-i] ‘peasant (adj)’; cf. [xwɔp] ‘peasant’) are simplified to a single affricate ([studɛn«ʦ»kʲ-i] ‘student (adj)’; Gussmann Reference Gussmann2007: 154).Footnote 3 It has also been argued that some apparent cases of segment deletion should instead be analysed as vacuous coalescence, whereby the fused output retains all the features of only one of the input segments. Vacuous coalescence has also been claimed to encompass cases of morphological haplology (Lawrence Reference Lawrence and Haraguchi1997, de Lacy Reference de Lacy, de Lacy and Nowak2000), in which an affix is absent in the context of a featurally identical or near-identical string.Footnote 4

The exact nature of reductive coalescence alternations has been the subject of considerable debate in phonological literature. One prominent claim is that coalescence is the effect of the interaction of two independent processes of assimilation and deletion, where deletion removes the source of the spreading feature, rendering assimilation ‘opaque’ (Kiparsky Reference Kiparsky and Dingwall1971, Reference Kiparsky and Fujimura1973). For example, Herbert (Reference Herbert1986: 252) analyses Austronesian nasal substitution as regressive nasal place assimilation followed by deletion of the triggering obstruent. A different analysis of Indonesian nasal substitution is suggested by McCarthy (Reference McCarthy2007: 88–91), who argues that it could be viewed as the opaque interaction of progressive nasality assimilation and deletion of coda nasals. Similarly, for hiatus resolution in both Xhosa (Aoki Reference Aoki1974) and Chumburung (Snider Reference Snider1989), analyses have been proposed in which a lowering rule affecting the second vowel in a sequence is made opaque by a later rule deleting the vowel that triggers lowering.

Other authors, however, have questioned whether this approach is feasible for all cases of reductive coalescence, citing typological and language-internal arguments. In this article, I follow Awobuluyi (Reference Awobuluyi1987) and Pater (Reference Pater, Kager, van der Hulst and Zonneveld1999) in assuming that while some patterns of coalescence, which I refer to as assimilatory, can be analysed as opaque interaction of assimilation and deletion, others (which I call compensatory) cannot. Below, I outline the diagnostics that have been proposed to differentiate between the two.

2.1.1 Assimilatory coalescence

Reductive coalescence has been argued to be assimilatory in nature when the language displays evidence for the presence of independent processes of assimilation and deletion whose interaction could yield the effect of apparent fusion of two segments. Such evidence can be found in two situations: (i) when the sets of strings affected by each of the putative processes do not fully overlap, and (ii) when the putative process of assimilation is applicable only to a subset of forms to which deletion applies, but assimilation can still be observed in isolation because the deletion rule is optional.

Alternations of the latter type can be found in some varieties of Modern Greek (such as the speech of older Athenian speakers, as described in Arvaniti Reference Arvaniti1999b and Arvaniti & Joseph Reference Arvaniti and Joseph2000), where at the juncture between certain proclitics (e.g. the accusative form of the feminine article /tin/ or the negative particles /ðen/ and /min/) and their hosts, a sequence of a nasal and a voiceless stop is optionally simplified to a single voiced obstruent, as in (5a.i). It may appear that the nasal and the stop have fused, with the resulting sound inheriting manner and place from the second segment and voicing from the first one. However, in forms in which the underlying nasal is retained, the stem-initial stop also surfaces as voiced, as shown in (5a.ii). This motivates an independent postnasal voicing process in the language. By the same token, nasal deletion can also be found in contexts where postnasal voicing is inapplicable. As shown in (5b), the final segment of the proclitics is also optionally deleted when followed by a voiced stop. Because nasal deletion targets the trigger of voicing, the apparent coalescence in (5a.i) can be interpreted as the result of the opaque interaction of these two processes (data from Arvaniti Reference Arvaniti1999b, Holton et al. Reference Holton, Mackridge and Philippaki-Warburton2004, Kalimeris et al. Reference Kalimeris, Mikros and Bakamidis2005).

  1. (5)

An example of assimilatory coalescence of the other type, where the sets of strings affected by two obligatory processes do not fully overlap, is offered by Snider (Reference Snider1989), who argues that the quality of the vowel resulting from simplification of hiatus formed across word boundaries in Chumburung in (2b) can be fully explained by reference to two postlexical spreading processes obscured by the application of vowel deletion. Both spreading processes are independently motivated by phrases in which hiatus does not arise. One is bounded progressive ATR vowel harmony affecting high [―ATR] vowels in the first syllable of a word preceded by a word whose last syllable contains a [+ATR] vowel, as in (6a.i). Another is a lowering process affecting words that begin with a high vowel when these are preceded by a word with a non-high vowel in the final syllable, as in (a.ii). Vowel deletion can be observed in isolation in phrases where vowel harmony and lowering are inapplicable, as in (b).

  1. (6)

As illustrated above, both Modern Greek and Chumburung have phonological processes whose opaque interaction could yield results identical to those of the genuine fusion of two segments. This raises the question of whether treating the data in (2b) and (5a.i) as the effect of a separate process of coalescence is warranted. The answer is clearly negative in rule-based approaches, where an evaluation metric based on the notions of economy and simplicity favours analyses in which complex patterns are derived from the interaction of few general rules. However, this kind of argument does not automatically translate into optimality-theoretic approaches, where positing an additional process does not involve adding a new rule to the grammar (which would increase its cost), but rather simply promoting the driving constraint to a position in which it can have an impact on the result of the evaluation. Nevertheless, an OT analysis that treats the alternations in (5a.i) and (2b) as unrelated to those in (5a.ii) and (6a, b) misses the generalisation that the spreading feature ([+ATR] and [―high] in Chumburung; [+voiced] in Modern Greek) is the same as the feature surfacing in the seemingly fused segment. In other words, the fact that the result of coalescence is a voiced obstruent in Modern Greek (rather than, say, a nasal stop, as in Austronesian nasal substitution) is treated as an accidental property of the grammar, unrelated to the presence of a voicing process in the language. To capture the apparent connection between the quality of the output segments in coalescence and in assimilation, the analysis should link the two processes.

2.1.2 Compensatory coalescence

Not all languages with reductive coalescence show evidence for independent processes of assimilation that could produce the effect of fusion when rendered opaque by a separate process of deletion. As pointed out by McCarthy (Reference McCarthy2007: 90), this in itself does not preclude treating a coalescence alternation as the result of the interaction of two processes whose structural descriptions just happen to be in a subset–superset relation, meaning that one of the processes can never be observed in isolation. However, two other kinds of criticism have been levelled at some analyses which decompose coalescence into assimilation and deletion.

One class of objections is typological: in some cases, one of the two interacting processes is never attested in isolation. This has been argued to be the case for the postnasal deletion of voiceless stops that would have to accompany regressive place assimilation to give the effect of nasal substitution. According to Pater (Reference Pater, Kager, van der Hulst and Zonneveld1999: 313–314), deletion of postnasal voiceless consonants is never observed without concomitant nasal place assimilation. The status of progressive nasalisation as a component of nasal substitution, as postulated by McCarthy, is less clear. Cross-linguistically, it is voiced obstruents that tend to undergo progressive nasalisation; voiceless obstruents in the same context generally undergo voicing instead (Hyman Reference Hyman, Hume and Johnson2001: 168–171, Recasens Reference Recasens2018: 147). However, in languages with nasal substitution, the process would have to be restricted to voiceless obstruents, as in Indonesian, where nasal + voiced consonant clusters surface faithfully. This kind of progressive nasalisation, which affects voiceless segments only, seems to be unattested without concomitant deletion of the triggering nasal.

The other type of arguments raised against assimilation + deletion analyses of coalescence alternations is language-internal: decomposition makes incorrect predictions for another part of the language, it misses a generalisation or the two processes seem to be inextricably linked, in the sense that if one of them fails to apply, so does the other (Stahlke Reference Stahlke1976). One example of such language-internal arguments against decomposition accounts can be found in Pater's (Reference Pater, Kager, van der Hulst and Zonneveld1999: 314) discussion of the putative postnasal deletion process in Indonesian, which would predict incorrect results for the interaction of nasal substitution with reduplication. Different problems arise with respect to McCarthy's decomposition of Indonesian nasal substitution into progressive nasality assimilation obscured by deletion of the trigger nasal. As argued by Pater (Reference Pater and Lombardi2001), nasal substitution applies exclusively at the left edge of a prosodic word, formed across a stem and a prefix. He interprets nasal substitution as a strategy to avoid a non-crisp ω edge, created by place assimilation across a ω boundary. This provides a natural explanation for the lack of coalescence in other contexts, for example, morpheme internally, (7a) or across a prefix–prefix boundary, (7b) (data from Lapoliwa Reference Lapoliwa1981: 60, Stevens & Schmidgall-Tellings Reference Stevens and Schmidgall-Tellings2010: 251–252).

  1. (7)

If nasal substitution is decomposed, the application of both nasal deletion and progressive assimilation has to be restricted to the relevant contexts. While morpheme-internal deletion could be blocked by reference to I-Contiguity (McCarthy & Prince Reference McCarthy, Prince, Beckman, Dickey and Urbanczyk1995: 371), it is less clear what could prevent it across a prefix–prefix boundary. Similarly, it is not clear how progressive nasalisation could be restricted to apply exclusively at a prefix–stem boundary.

2.2 Non-reductive coalescence

In addition to examples of coalescence similar to those described in the previous section, the literature contains reference to a different kind of fusion process, affecting adjacent identical or partially identical segments. This type of coalescence, which I refer to as non-reductive, often cannot be identified by looking at the phonetic realisation of the string, because the output contains the same number of segments as the input, with the same featural and tonal specifications. What distinguishes segments that have undergone non-reductive coalescence from those that have not is their phonological behaviour, with segments that have undergone the process behaving as a single unit for the purposes of other processes. This has been argued for adjacent tones and adjacent identical consonants.

A classic example from the domain of tone is offered by Myers (Reference Myers1987, Reference Myers1997) in his analysis of tonal patterns in the Zezuru dialect of Shona. Myers argues that the effect of Meeussen's Rule (Goldsmith Reference Goldsmith, Aronoff and Oerhle1984) in the dialect is best explained by the assumption that the process is preceded by fusion of adjacent underlying high tones into a single high tone. In Zezuru Shona, the application of Meeussen's Rule at the word level lowers a span of adjacent high-toned syllables, even when they are heteromorphemic, as in (8). (All Shona data in the paper are from Myers (Reference Myers1987, Reference Myers1997). The language has two level tones – high (ˊ) and low ( ) – and no contrastive contour tones. Square brackets indicate the boundaries of the constituents juxtaposed at the word stratum.)

  1. (8)

Myers (Reference Myers1997) provides evidence to show that the process is driven by a syllable-mediated OCP constraint, which penalises adjacent high tones associated to adjacent syllables. This means that in the examples in (8) it should be enough to lower the tone on just one of the syllables, giving *[í] [bangá], for example, rather than [í] [banga]. Myers explains the fact that the entire tonal span is affected by arguing that the high tones fused at a previous stratum. Thus, at the point at which Meeussen's Rule applies, it affects a single tonal element. Since this element is now associated to more than one syllable, the process has the effect of lowering an entire span.

Non-reductive coalescence has also been posited to explain a number of nearly universal characteristics of morpheme-internal geminates, such as geminate integrity and full alterability. Geminate integrity (Leben Reference Leben1980, Steriade Reference Steriade1982, Hayes Reference Hayes1986b, Schein & Steriade Reference Schein and Steriade1986) refers to the observation that epenthesis processes that break up consonant clusters tend not to affect geminate consonants, while full alterability (Keer Reference Keer1999) concerns the fact that feature-changing processes targeting structures present in a geminate in some lefthand environment tend to affect the entire geminate. Both facts can be explained if geminates are represented as a single melody associated to two timing units. This representation can be arrived at by coalescence of adjacent identical consonants.

3 Proposal: coalescence as spreading and delinking

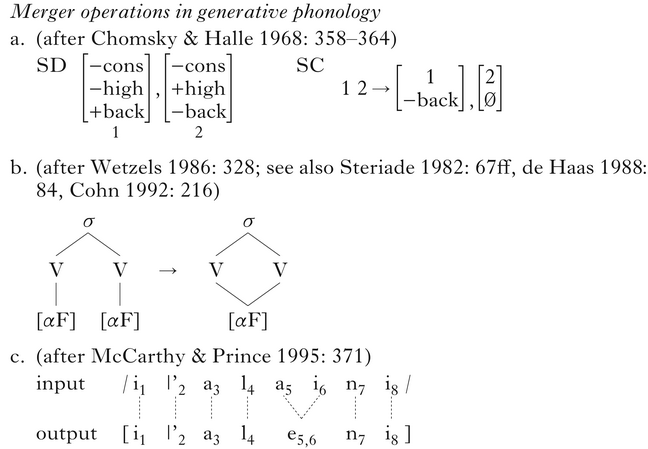
As shown in the previous section, a number of natural languages show alternations in which two input elements seem to fuse into one. Many theories of phonology have a dedicated operation designed specifically to deal with this type of alternation, for example a rewrite rule such as (9a), which replaces two segments with one, an autosegmental node merger rule or convention, as in (9b), or two-to-one mapping in optimality-theoretic Correspondence Theory, such as (9c).

  1. (9)

This kind of operation is not easy to implement in optimality-theoretic approaches to phonology that reject the Correspondence Theory view on the relation between the input and output, such as Coloured Containment Theory, and instead adopt the principle of containment, which holds that the input is a substructure of the output. In Coloured Containment Theory, the ways in which the phonological component can modify its input are highly limited. Gen can only create output candidates by adding elements of representation (autosegmental nodes and association lines) to the input and delinking underlying association lines, leading to the non-pronunciation of underparsed nodes. It does not rewrite substructures of the input, and therefore cannot remove, reorder or modify objects. By the same token, it cannot replace two objects with a single one.

In this section, I show that it is possible to analyse the three types of coalescence identified in §2 using the tools available in Coloured Containment Theory. The proposed analysis treats coalescence as the result of the underparsing of some autosegmental nodes (by virtue of either not linking them to higher prosodic structure or delinking underlying association lines), which results in their non-pronunciation, and adding new association lines between others. The resulting output structures are illustrated schematically in (10). In reductive coalescence, in (a), the reassociated autosegment is the daughter of the underparsed node. In the output, it docks onto a new host on the same tier as its phonetically unrealised mother. In non-reductive coalescence, in (b), a new association line is added between a sister of a delinked autosegment and the node that underlyingly dominates that autosegment.

  1. (10)

The output structures in (10) are reminiscent of pre-OT autosegmental analyses that treat assimilation as the effect of a delinking-cum-spreading operation (e.g. Halle & Vergnaud Reference Halle and Vergnaud1980, Steriade Reference Steriade1982: 42, Kiparsky Reference Kiparsky1985: 98, Hayes Reference Hayes1986a, Schein & Steriade Reference Schein and Steriade1986, de Haas Reference Haas1987: 188). However, in contrast to the rule-based analysis, in which delinking-cum-spreading is viewed as a single, though composite, structural change carried out in a single environment, in the analysis proposed here each of the subcomponents of coalescence (underparsing and spreading) are independent operations, driven by distinct constraints. Which constraints these are depends on the type of coalescence and processes involved.

In all types of coalescence, the underparsing subcomponent is the effect of a high-ranked markedness constraint that either (i) drives the delinking of some part of a marked structure or (ii) blocks the insertion of association lines leading to such a structure. In reductive coalescence, the driver is a sequential or syllable markedness constraint that can be satisfied by deleting a segment. In non-reductive coalescence, the driver of delinking is an OCP constraint prohibiting adjacent identical elements of a certain kind (Leben Reference Leben1973, Reference Leben and Fromkin1978, McCarthy Reference McCarthy1986, Myers Reference Myers1997).

The constraints driving the spreading subcomponent also depend on the type of coalescence. In compensatory coalescence, a high-ranked constraint mandating that some underlying feature be realised phonetically (Max[F]) enforces the reassociation of that feature when its dominating node is deleted. In assimilatory coalescence, adding an association line between a feature and another host is driven by a constraint from the Share family (McCarthy Reference McCarthy, Goldsmith, Hume and Leo Wetzels2010: 200), which, irrespective of whether they are pronounced or covert, penalises adjacent root nodes that do not share a certain feature. When the original host is not phonetically realised, spreading is opaque. In non-reductive coalescence, spreading is driven by a constraint from the Specify family, requiring that a certain node dominate a node on some lower tier. The domain of spreading is restricted to those hosts that have lost their daughters by means of a constraint penalising segments (or tone-bearing units) specified for the spreading feature, either covertly or overtly.

The effect of the abovementioned constraints in analyses of complementary, assimilatory and non-reductive coalescence is illustrated in §3.2, §3.3 and §3.5 respectively, with an excursus on vacuous coalescence in §3.4. But first, the basic tenets of Autosegmental Coloured Containment Theory are presented in §3.1.

3.1 Basic principles of Autosegmental Coloured Containment Theory

3.1.1 Representations

Autosegmental Coloured Containment Theory (ACC; Trommer Reference Trommer2011, Reference Trommer2014, Trommer & Zimmermann Reference Trommer and Zimmermann2014, Zimmermann Reference Zimmermann2013, Reference Zimmermann2017) is a revised implementation of the original version of OT proposed by Prince & Smolensky (Reference Prince and Smolensky1993). The framework adopts the standard representational assumptions of autosegmental phonology (Goldsmith Reference Goldsmith1976, Reference Goldsmith1990, McCarthy Reference McCarthy1979, Pulleyblank Reference Pulleyblank1986, Reference Pulleyblank1989), where phonological objects occupy positions on independent tiers, but may be linked by means of association lines. These objects (which I will collectively refer to as ‘nodes’) include segmental and tonal features (e.g. [+voiced], [―nasal], H), organisational nodes (e.g. the root node (•) and the place node) and higher prosodic units (e.g. the syllable (σ) and the phonological word (ω)). A further assumption is that phonological nodes are organised hierarchically, with nodes at higher-level tiers immediately dominating the nodes at lower-level tiers that they are associated with.

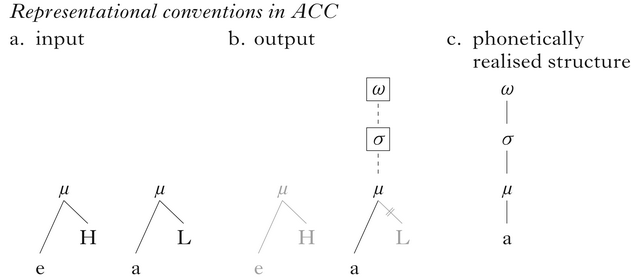
A core principle of Containment Theory is the assumption that autosegmental nodes can never be removed. Underlying nodes that seem to have undergone deletion are still present in the output, but are not interpreted in the post-phonological phonetic component, and are therefore not pronounced. Such elements have to be indicated in some way. This is usually done by adopting a convention akin to the concept of Stray Erasure (McCarthy Reference McCarthy1979, Steriade Reference Steriade1982, Itô Reference Itô1986, Reference Itô1989), which states that autosegments that are not properly integrated into higher prosodic structures are not pronounced. ACC extends the containment principle to association lines, requiring that these, too, not be removed from the input. To be able to express delinking of two underlyingly associated nodes, ACC expands its representational toolbox by adding a binary visibility parameter to association lines, and allowing the phonology to mark underlying association lines as invisible. Under this assumption, properly integrated and hence phonetically realised nodes are those that are linked to the highest prosodic node through an uninterrupted path of visible association lines. If a node is not linked to a higher structure at all, or if some of the association lines in the path linking it to the highest node are marked as invisible, it is not interpreted by the phonetic component.

The final representational assumption concerns morphosyntactic information. ACC adopts the theory of morphological colours (van Oostendorp Reference Oostendorp2003, Reference Oostendorp2006, Reference Oostendorp2007, Reference Oostendorp2008, Revithiadou Reference Revithiadou2007), in which every morpheme is assumed to have a unique identifier, referred to as its colour.Footnote 5 All phonological elements – nodes and association lines – that form part of a morpheme share its colour. Morphological colouring means that the phonology is able to distinguish between elements belonging to different morphemes, as well as between underlying and epenthetic elements, as the latter are not affiliated with any morpheme and are therefore colourless. ACC departs from the original implementation of the containment idea, the Parse/Fill model, in which epenthetic segments are represented as empty prosodic positions, in allowing all phonological elements (association lines, prosodic nodes and features) to be inserted. This addresses objections raised against the previous treatment of epenthesis, where the quality of epenthetic material was determined by a post-phonological interpretive component. The assumption of colour in ACC can afford special formal status to any epenthetic element, thus allowing for reference to the quality of epenthetic material by markedness constraints.

(11) shows the graphical conventions used in ACC to indicate epenthesis, delinking and proper integration, using the hypothetical input /é-à/. In the output, prosodic structure has been built over the second mora. Epenthetic nodes (σ and ω) are set off in boxes, and epenthetic association lines are dashed (morphological colour is not indicated in the paper, as it will not be directly relevant to any of the analyses). The association line linking the righthand mora to the low tone in the input is marked as invisible and, as a result, the tone remains unpronounced, although it is still present in the output form. The invisibility of the association line is indicated by ‘=’. Additionally, for ease of identification, phonetically uninterpreted association lines and nodes are in grey. (11) also demonstrates that being linked to a higher node is not a sufficient condition for phonetic realisation. Even though the lefthand vowel and tone are both associated to a mora with visible association lines, the mora is not linked to any higher structure. Consequently, the entire structure remains unpronounced.

  1. (11)

3.1.2 Candidate generation

In classical OT with Correspondence, Gen, which is responsible for providing candidate output forms for a given input, can be thought of as supplying correspondence relations between elements (typically, individual segments) of that input and all members of the universal set of all possible structures over some alphabet (McCarthy & Prince Reference McCarthy, Prince, Beckman, Dickey and Urbanczyk1995: 263, McCarthy et al. Reference McCarthy, Kimper and Mullin2012: 178). In ACC, Gen has to be reconceptualised. It is interpreted as a component that produces output candidates by performing one or more basic operations on an underlying form. The set of licit operations is limited to those in (12).

  1. (12)

Every phonological process can be decomposed into one or more of the primitive operations in (12). For example, epenthesis involves inserting a node (operation (a)) and associating it to the remaining structure by inserting a colourless association line (operation (b)). Feature spreading involves inserting colourless association lines between nodes that are not associated in the input, while deletion (or, strictly speaking, phonetic non-realisation resulting from underparsing) involves either not inserting association lines to link the given node to higher structures (not operation (b)) or marking such association lines as invisible (operation (c)). In the present proposal, phonological coalescence is decomposed into the insertion of an association line between some nodes (operation (b)) and the underparsing of others (operation (c)/not operation (b)).

3.1.3 Markedness constraints and the Cloning Hypothesis

In ACC, covert material may influence the realisation of phonetically realised structures, leading to opacity (Kiparsky Reference Kiparsky and Dingwall1971, Reference Kiparsky and Fujimura1973), where the reason for the application or non-application of some phonological process is obscured in the surface form (here the output of the phonetic component). This influence can be exerted exclusively by a class of general markedness constraints (or ‘clones’), which assess the well-formedness of the entire output form, including invisible association lines, and nodes that are not properly integrated into higher prosodic structure. I follow Trommer (Reference Trommer2011) in assuming that the range of possible general markedness constraints is restricted to clones of articulatorily, perceptually or computationally grounded phonetic markedness constraints, sensitive to overt (i.e. visible and properly integrated) parts of the output form, as in (13), adapted from Trommer (Reference Trommer2020: 10).

  1. (13)

The most important difference between the two classes of constraints is that general clones are insensitive to delinking and improper integration. Since they treat overt and covert material on a par, a structure that is evaluated as ill- or well-formed by a general clone is equally ill- or well-formed if association lines belonging to this structure are marked as invisible. Phonetic clones, in contrast, do not mark the target structure as ill- or well-formed if some part of this structure is not realised phonetically. As will be shown in what follows, this property of general clones makes it possible for covert structures to act as opaque drivers or opaque non-blockers, leading to overapplication opacity (McCarthy Reference McCarthy1999, Baković Reference Baković2007), or as opaque blockers, leading to underapplication.

3.2 Compensatory reductive coalescence

Recall that in reductive coalescence two underlying segments are simplified to one, which typically bears features from each of the input segments. I analyse this as underparsing of one of the root nodes, coupled with the reassociation of a feature or features from the underlying host to a neighbouring one; cf. (10a). In compensatory reductive coalescence, underparsing and reassociation seem inextricably linked, with no evidence for independent processes of deletion and assimilation whose interaction could produce the effect of fusion.

I propose that compensatory coalescence should be analysed as a subclass of a broader phenomenon of autosegmental stability under deletion. Stability effects, first discussed by Goldsmith (Reference Goldsmith1976) as an argument for autosegmental representations, refer to situations in which elements on some tier or tiers are deleted, but elements on lower tiers to which the deleted elements were associated are preserved. Although most commonly discussed in reference to tonal patterns, stability effects have been argued to extend to other autosegmental tiers, including the skeletal or moraic tier (Hayes Reference Hayes1989) and featural tiers (e.g. Mascaró Reference Mascaró, Wetzels and Sezer1985, Prunet Reference Prunet1986, Wetzels Reference Wetzels1995, Vaux Reference Vaux1998). This idea was extended to patterns of reductive coalescence in early OT analyses of hiatus resolution (Casali Reference Casali1996) and patterns of consonantal coalescence in Navajo and Chipewyan (Causley Reference Causley1997). This section presents an ACC adaptation of an analysis of Xhosa vowel coalescence outlined by Casali (Reference Casali1996) as a means to familiarise the readers with the notations and conventions used in the article, and to serve as a basis for later comparison with the analysis of assimilatory coalescence in §3.3 and for further theoretical discussion in §4.

In reductive coalescence, underparsing, resulting in a reduction in the number of phonetically realised host nodes, is the effect of a high-ranked markedness constraint satisfied by a candidate in which an underlying root node fails to be integrated into higher prosodic structure. The identity of the markedness constraint depends on the segments forming the penalised structure; for all alternations discussed here, the driver can be assumed to be a sequential or syllable markedness constraint. For hiatus resolution, as in Xhosa and Chumburung in (2), the constraint is *Hiatus in (14) (adapted from Pulleyblank Reference Pulleyblank and Bobda2008: 127), which prohibits adjacent vowels. The constraint is a phonetic clone, indicated by underlining. The phrase ‘in P’ in the definition refers to P-structure, i.e. the overt part of an output candidate.

  1. (14)

To block the prosodification of one of the input root nodes, the markedness constraint has to outrank faithfulness constraints that are violated by underparsing. Here, the relevant constraint is Max(•) in (15a), which penalises covert underlying material (here, coloured root nodes that are not properly integrated).Footnote 6

  1. (15)

Max(•) and other faithfulness constraints violated by underparsing have to be outranked by faithfulness and markedness constraints that militate against other hiatus-resolution strategies, such as consonant epenthesis, which is prohibited by Dep(•) in (15b). Additionally, the driver has to be supplemented by constraints that govern the directionality of deletion (i.e. whether the first or the second segment in a sequence is not prosodified; for example, underparsing the leftmost rather than the rightmost H node in (10a)). Casali (Reference Casali1996: 27, Reference Casali1997: 508) proposes an account in which the deletion of the first vowel in a sequence spanning the root–suffix boundary is favoured by a positional faithfulness constraint requiring the preservation of morpheme-initial segments. An ACC version of this constraint protects the leftmost element in a span of nodes with the same morphological colour, as in (16).Footnote 7

  1. (16)

The interaction of the constraints discussed above can be illustrated with a set of Xhosa forms in which hiatus is resolved by deletion, rather than coalescence, such as those in (17), where the high front stem-final vowel is deleted before the initial vowel of the locative suffix /-ini/.

  1. (17)

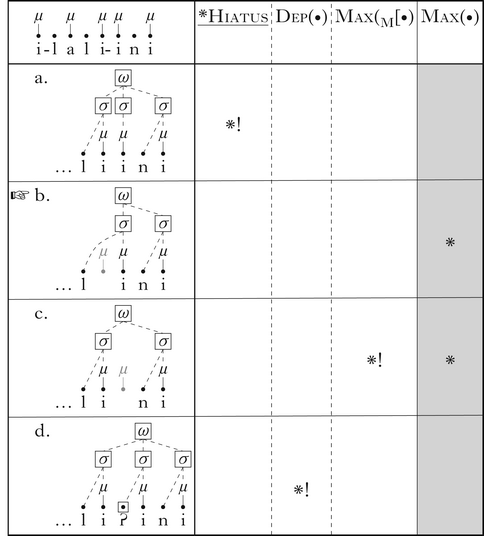
The tableau in (18) shows the evaluation of the word /i-lali-ini/ → [elalini] ‘village (loc)’.

  1. (18)

If all parts of the input are fully integrated into higher prosodic structure, as in candidate (a), *Hiatus is fatally violated. The winning candidate, (b), avoids this violation by leaving the stem-final root node unsyllabified. This results in the non-realisation of the first vowel in the sequence and the violation of Max(•). Candidates that involve other ways of circumventing the violation of *Hiatus are either harmonically bounded, like (c), in which the failure to integrate the suffix-initial root node incurs a superfluous violation of the positional faithfulness constraint Max(M[•), or fall foul of higher-ranked constraints, like (d), where splitting the vowel sequence with an epenthetic consonant violates Dep(•).

In coalescence alternations, the non-pronunciation of a root node is accompanied by the reassociation of some features underlyingly dominated by that root node onto a different, phonetically realised, host. In Xhosa hiatus resolution, this feature is [―high]. In an OT analysis that treats the reassociation as a stability effect, the operation is driven by a high-ranked constraint mandating that some underlying node be realised phonetically. Here, the relevant constraint is Max[―high], whose ACC definition is given in (19).

  1. (19)

Compensatory coalescence arises when separate Max constraints require the preservation of two disconnected nodes that form part of (or are dominated by) the same marked structure. Repairing the structure by deleting one segment would violate some Max[F] constraint; deleting another segment would violate another feature-preservation constraint (Max[G]) or a positional Max constraint. Reassociating the feature protected by Max[F] from its host to a node protected by positional faithfulness (or to a node dominating another protected feature) and deleting the host is a win–win strategy that makes it possible to retain both protected nodes while repairing the marked structure. This is shown in (20) for the Xhosa word /i|’ala-ini/ → [e|’aleni] ‘side (loc)’.

  1. (20)

As in (18), *Hiatus is fatally violated by the segmentally faithful candidate, (a). The newly introduced featural faithfulness constraint Max[―high] eliminates candidate (b), in which the first vowel in the hiatus is deleted.Footnote 8 Deleting the suffix-initial high vowel, as in candidate (c), incurs a fatal violation of Max(M[•). The coalescence candidate, (d), is optimal, because it retains both the suffix-initial vowel and the [―high] feature, at the cost of violating low-ranked Max(•) and Max[+high].

The same type of analysis can be applied to other patterns of compensatory coalescence, such as nasal substitution in Indonesian (cf. (3)), where Max[+nas] would drive the reassociation subcomponent. Non-local coalescence patterns, such as the one in Chaha in (4), where the back glide fuses with the nearest preceding labial or velar segment, are also amenable to an analysis in terms of feature stability, here driven by Max[+round]. Long-distance reassociation can be enforced by a segmental markedness constraint which prevents certain combinations of features. Since the [+round] feature in Chaha docks onto velars or labials, the relevant constraint is *[cor]ʷ in (21), which penalises labialised coronals.

  1. (21)

The fact that a feature can reassociate onto a non-adjacent host raises the question of how the locality of reassociation should be constrained, not only in Chaha, where the feature lands on a suitable segment closest to the underlying host, but also in languages where coalescence is fully local, with reassociation only allowed between underlyingly adjacent segments. To this end, ACC has two constraint families at its disposal, NoSkipping in (22a), which penalises skipping nodes in association, and NoCrossing in (22b), which penalises crossing association lines (cf. Trommer Reference Trommer2011: 54).

  1. (22)

The directionality of reassociation is governed by a class of constraints that penalise epenthetic association to nodes preceding or following an underlyingly associated node, as in (23).

  1. (23)

The effect of these constraints is shown in (24) for Chaha /gəfər-w-p-a-m/ → [gəfʷərpam] ‘one released to her detriment’ (Banksira Reference Banksira2000: 29). I assume that the deletion subcomponent of coalescence is driven by constraints on syllable structure, collectively referred to as Syll: *Complex, penalising complex syllable margins, and *Coda(G), violated by glides in the coda position. To save space, (24) and the following tableaux only include detailed phonological representations of the relevant segments, and the specifications for some features are shown above the root nodes that dominate them. All prosodic structure above the level of the root node is omitted. A greyed-out node on the highest tier shown should be taken to be unintegrated into any higher structure, by analogy with the greyed-out root nodes in (18) and (20).

  1. (24)

The fully prosodified candidate, (a), violates a constraint governing syllable structure (depending on the syllabification, either *Complex or *Coda(G)), while candidate (b), in which the underlying glide is left unsyllabified, falls foul of the Max constraint protecting the feature [+round]. In the remaining candidates, the feature is rescued by reassociation to a different segment in the word. In candidates (c) and (d), the reassociation is local, leading to violation of high-ranked constraints controlling the directionality of reassociation, (c), or the quality of segments in the surface inventory, (d). The directionality constraint is a general clone, which assesses the entire output form. Consequently, it is violated by the rightward spreading, even though one of the association lines involved in the marked structure is not realised phonetically. The same is true of the NoSkipping constraint, which ensures that the feature [+round] lands on the rightmost non-coronal consonant that underlyingly precedes the source of the feature, (e), rather than one further away, (f).Footnote 9 Even though the overt subparts of the two candidates do not include a [+round] feature shared between two non-adjacent root nodes, this configuration is covertly present in each candidate, and incurs as many violations of NoSkipping as there are root nodes separating the original and the new host.

3.3 Assimilatory reductive coalescence

Constraints from the Max[F] family make it possible to account for most examples of reductive coalescence, and could in principle be used to derive patterns of assimilatory coalescence, such as those in Chumburung in (2b) and Modern Greek in (5a.i). Nevertheless, as pointed out in §2.1.1, viewing coalescence as the result of the opaque interaction of assimilation and deletion does seem warranted in some cases. Treating such patterns as cases of feature stability has a drawback, in that it fails to express the relationship between the quality of the feature preserved in coalescence and the quality of the feature that spreads in an independently observed process of assimilation.

ACC offers a way to link the two. Recall that in this framework, covert material, which remains unpronounced but is nevertheless present in the output, can affect the shape of overt material via general markedness constraints, i.e. clones of independently motivated phonetic constraints that assess the entire structure, not just its properly integrated subpart. This makes it possible to treat assimilatory coalescence as a case of the overapplication of assimilation, whereby the process is driven by a constraint that demands spreading of a given feature irrespective of whether its host is properly integrated (and hence phonetically realised). In ACC, opaquely driven overapplication opacity is effected by general clones of positive markedness constraints, which penalise structures lacking a certain property, and can therefore drive its insertion or spreading.

Under the assumption that postnasal voicing in Modern Greek is an NC̥ effect, the (opaque) spreading of [+voice] can be driven by a positive reformulation of Pater's (Reference Pater, Kager, van der Hulst and Zonneveld1999) *NC̥ constraint (which assigns a violation for every nasal stop followed by a voiceless obstruent) as a constraint of the Share family (McCarthy Reference McCarthy, Goldsmith, Hume and Leo Wetzels2010: 200, Trommer Reference Trommer2011: 230), which penalises adjacent segments in a nasal–obstruent sequence that are not associated to the same [+voice] node, as in (25).Footnote 10

  1. (25)

I follow Arvaniti (Reference Arvaniti1999a) in assuming that Modern Greek deletion is driven by *Coda. As shown in the evaluation of the relevant fragment of /tin ˈkɐpɐ/ → [ti ˈgɐpɐ] in (26), the constraints mentioned above are sufficient to account for the voicing + deletion pattern in Modern Greek.Footnote 11

  1. (26)

In (26), the faithful candidate, (a), violates two high-ranked markedness constraints, Share[+vd]NC and *Coda. In candidate (b), voicing spreads from the nasal onto the following stop, which satisfies Share[+vd]NC. However, the coda nasal still violates *Coda. In (c), the nasal is not prosodified. This leads to *Coda being satisfied, but not Share[+vd]NC, since the latter constraint assesses the entire output structure, which still contains a sequence of root nodes that do not share the [+voice] feature. The optimal output is candidate (d), in which voicing spreads from the covert nasal.

The same kind of analysis, with the general clone of a positive markedness constraint driving the spreading of a feature from a phonetically unrealised source, can be applied to vowel coalescence in Chumburung in (2b). In addition to the presence of independently motivated processes of vowel deletion in (6b) and spreading of the features [+ATR] and [―high] in (6a), the language provides theory-internal evidence against treating the reassociation of [+ATR] in terms of feature stability driven by a Max[+ATR] constraint. First, the two assimilatory processes illustrated in (6a) interact in an opaque manner: although progressive ATR harmony does not normally affect [―high] vowels (e.g. [bùnì bàsà] ‘butterfly's needle’, [bùnì bɔ̀tɪ́] ‘butterfly's sack’; Snider Reference Snider2018: 122–123), it does apply to mid vowels derived from high ones by the lowering process, as evidenced by the first example in (6a.ii). As explained above, an ACC account of this type of overapplication requires the constraint driving progressive ATR harmony to be a positive general clone. If this is the case, then the process is predicted to overapply not only when the target vowel is lowered, but also when the source vowel is not realised phonetically, producing the effect of coalescence, as in the phrase /ìwú ɪ̀sá/ → [ìwí↓sá] ‘three thorns’. Under these circumstances, adding a Max[+ATR] constraint to the evaluation has no effect on the outcome. A further potential problem for an ATR-stability analysis (noted by Casali Reference Casali1990: 337 in his discussion of possible [+round] stability in Nawuri) is that, due to a word-level harmony process, all vowels within a Chumburung word (save for syllable-final low vowels) have the same [ATR] value. If word-level harmony is understood as sharing a single [ATR] feature, then deleting the last vowel in a polysyllabic word does not lead to a violation of Max[+ATR], and reassociation is not expected. Since in Chumburung, [+ATR] reassociates even when the first word is polysyllabic (as in /ìpésí ɪ̀sá/ → [ìpésí↓sá] ‘three brooms’; Keith Snider personal communication), an analysis that treats [+ATR] reassociation as a genuine case of assimilatory coalescence seems more appropriate.

3.4 Excursus: vacuous coalescence

As noted in §2.1, some instances of apparent segmental deletion have been argued to involve vacuous coalescence instead. In some cases, the deletion analysis is a by-product of the correspondence-theoretic constraint ranking. As pointed out by Wheeler (Reference Wheeler2005a), languages in which sequences of segments are simplified in the same context by either coalescence or deletion, depending on the quality of the segments involved, require that both types of reduction be treated as a two-to-one mapping. This is because a correspondence-based analysis necessitates a ranking in which any constraint violated by a coalescence candidate, such as Uniformity, is ranked lower than constraints militating against other repairs, including Max, which penalises segmental deletion. In deletion contexts, this ranking will eliminate candidates in which one input segment has no output correspondents, in favour of coalescence candidates in which an output segment corresponds to two inputs, but happens to preserve all features of only one of them.

As illustrated by the analysis of Xhosa hiatus resolution in §3.2, this ‘once coalescence, always coalescence’ interpretation of segment-reduction patterns is not necessary in the proposed account. In words in which the first vowel in hiatus is [+high], the optimal candidate is one in which one root node, together with all the features it dominates, remains unpronounced, as in (18). It is only when the first vowel in hiatus is [―high] that underparsing of the root node is accompanied by reassociation of the protected feature to a neighbouring host, producing the effect of coalescence, as in (20). Nevertheless, ACC still makes it possible to describe a kind of vacuous coalescence involving vacuous spreading, where the reassociating feature lands on a segment dominating a feature with an identical value. In contrast to the correspondence-based analysis, however, such a candidate does not have to be the winner, as it can be eliminated by a high-ranked constraint against root nodes dominating identical features.

In addition to analyses involving vacuous coalescence as a ‘by-product’, arguments have been put forward for analysing some segment–zero alternations as cases of crucial vacuous coalescence, on the basis of language-internal or typological evidence against deletion accounts. One case in point is the reduction of syllable-final homorganic clusters in (Central) Catalan, as in [punˈt-ɛt] ‘bridge (dim)’ vs. [pɔn] ‘bridge’ (Wheeler Reference Wheeler2005a, Reference Wheeler2005b: 221). Baković (Reference Baković2017) argues that treating this pattern as coalescence makes it possible to uphold his theory of antigemination (Baković Reference Baković2005), which states that avoidance of ‘sufficiently similar’ adjacent consonants is the result of the interaction of two constraints: NoGem, a strict antigemination constraint against fully identical adjacent consonants, and some constraint enforcing assimilation of the features ignored in the determination of identity (e.g. Agree or Share). Catalan homorganic cluster reduction constitutes a prima facie counterexample to this theory, since it incorrectly predicts that all but place features should assimilate in the language. Baković (Reference Baković2017) points out that this prediction is not made if the Catalan pattern is treated as coalescence driven by a constraint against complex codas. In this case, the reduction is not the result of avoidance of segments that are similar enough. Rather, all sequences of tautosyllabic segments are disfavoured, but only those that have the same place of articulation can be fused, as this does not involve loss of featural information.

There are two ways to retain Baković's (Reference Baković2017) insight in an ACC analysis, and thus treat the reduction as driven by *ComplexCoda ranked above Max(•). One is to assume that Catalan cluster simplification involves vacuous spreading and that the surface segment dominates two identical place nodes (e.g. [coronal] in [pɔn]). This makes it possible to block deletion of segments in heterorganic clusters by ranking two constraints above *ComplexCoda: Max[place], which ensures that deletion can only apply if the place features dominated by the deleted root node can be associated with another, properly integrated, host, and *Contour, which militates against root nodes dominating non-identical place features. Another way to view the data is to assume that segment deletion is preceded by non-reductive coalescence (discussed in §3.5), resulting in homorganic sequences sharing a single set of place features. In this case, cluster reduction of heterorganic codas can be blocked by a Max[place] constraint. The constraint is satisfied when a segment in a homorganic sequence is deleted, because the place feature it dominates is still properly integrated, thanks to its association to the retained host.

Another kind of data that has been argued to involve crucial vacuous coalescence pertains to morphological haplology, where an affix or a part thereof apparently fails to surface in the context of a featurally identical or near-identical string. De Lacy (Reference de Lacy, de Lacy and Nowak2000) argues for an analysis in which haplology is driven by a general markedness constraint, such as *Struc, rather than any specific identity-avoidance constraint. *Struc is satisfied by fusion of identical segments, as this is the only way to reduce structure without loss of featural information. De Lacy provides evidence against treating at least some cases of morphological haplology, in Japanese and in French, as the result of deletion of the repeated material, either from the stem or from the affix. In Japanese, the evidence is related to the way haplology interacts with accentuation, while in French it is related to the restrictions on the shape of morphemes that can haplologise.

An attempt at an ACC analysis of morphological haplology that treats it as vacuous spreading of individual features or subsegmental nodes (as suggested above for the place node in Catalan) is unlikely to be successful, as it would involve massive violations of constraints on locality, making it impossible to restrict haplology to adjacent strings. However, the framework offers a different way to derive the patterns described by de Lacy, by extending the ACC analysis of subtractive morphology developed by Zimmermann (Reference Zimmermann2013, Reference Zimmermann2017) and Trommer & Zimmermann (Reference Trommer and Zimmermann2014) to morphological haplology. In their proposal, subtractive morphology (shortening or deletion of a segment or segments) is attributed to the affixation of a prosodically defective morpheme, which either lacks some prosodic structure (a mora or a syllable) or consists of floating prosodic nodes that are not associated to any melody. An analysis of haplology in these terms could treat it as the affixation of drifting melodic material to stems prosodified at a previous stratum, resulting in the affix ‘usurping’ some of the stem's prosodic nodes, leading to delinking of the melody that they underlyingly dominate. In contrast to general subtractive morphology, usurpation would have to be controlled by *Contour constraints which would only allow association to prosodic nodes affiliated with the stem if the segments dominated by those nodes are identical.

While a full analysis of haplology as subtractive morphology would take us too far afield, I briefly outline how this approach could be used to analyse Japanese and French haplology in terms of the underparsing of stem material. In Japanese, haplology affects the Classical Japanese predicative suffix [-ɕi], which repels a stem-final accent in underlyingly accented stems, shifting it to the stem-penultimate syllable, e.g. [ɕíɾo-ɕi] ‘white (classical.pred)’ vs. [ɕiɾó-i] ‘white (modern.pred)’ (Lawrence Reference Lawrence and Haraguchi1997: 382). When the suffix is attached to accented stems ending in [ɕi], the haplologised form carries the accent on the penultimate syllable, e.g. [ɯɾé«ɕi»] ‘happy (classical.pred)’; cf. [ɯɾeɕí-i] ‘happy (modern.pred)’ (Lawrence Reference Lawrence and Haraguchi1997: 382). According to de Lacy, this argues against deletion of stem material, as it would predict accent shift to the stem-initial vowel (*[ɯ́ɾe∅-ɕi]). A containment-based account, however, makes it possible to view the haplologised form as one in which the stem syllable is not realised phonetically, but is nevertheless counted by the accent shift if the constraint that drives it is a general clone sensitive to the entire output structure.

In French, haplology affecting words formed with the nominal derivational suffix /-ist/, e.g. /bodis/ ‘Baudis (name)’ + /ist/ → [bod«is»t], /maʁini/ ‘Marini (name)’ + /ist/ → [maʁin«i»st] (Corbin & Plénat Reference Corbin and Plénat1992, de Lacy Reference de Lacy, de Lacy and Nowak2000), fails to apply when the stem ends in [ist], that is, when it is fully identical to the suffix, e.g. /ametist/ ‘amethyst’ + /ist/ → [ametistist], *[amet«ist»]. According to de Lacy, this speaks against viewing the process as deletion of the stem material, as it makes is impossible to block deletion when it would result in the non-realisation of a morpheme. In a usurpation account, where the suffix is represented as a melody without any prosodic structure, attached to prosodified stems, the restriction can be reinterpreted as a ban, enforced by a general clone constraint on syllable codas, on associating a fricative to a (covert) coda containing an obstruent cluster with falling sonority.

3.5 Non-reductive coalescence

Non-reductive coalescence affects two or more identical lower nodes in a feature-geometric tree, yielding a single node that is associated to multiple immediately dominating nodes. I propose that this type of coalescence should be decomposed into two operations: (i) delinking of all but one of the lower nodes in a sequence of adjacent identical nodes, leaving them uninterpreted phonetically, and (ii) spreading the remaining, phonetically realised, node onto the hosts that have lost their daughters, as in (10b).

I illustrate my account with a reanalysis of high-tone coalescence in Zezuru Shona, which, as noted in §2.2, has two level tones, high (ˊ) and low ( ). When a sequence of high tones is created across a stem boundary, one of two word-level lowering processes applies. If a high-toned stem is preceded by a sequence of more than one consecutive high-toned syllable, the last one of these is lowered by a process that Myers (Reference Myers1987, Reference Myers1997) calls Tone Slip, illustrated in (27a). If the stem is preceded by a single high-toned syllable, Meeussen's Rule lowers the tone of the stem, as in (b) (cf. (8) above).

  1. (27)

Meeussen's Rule treats a sequence of adjacent high-toned syllables within a stem as a single unit, which results in lowering of the entire span. Myers accounts for this by arguing that the high tones had fused at the previous stratum. At the point at which Meeussen's Rule applies, the sequence of syllables is associated to a single high-toned node. A constraint protecting the left edge of a tonal span, Anchor(H)-L, ranked higher than Max(H), eliminates candidates in which only the leftmost stem syllable is lowered, favouring instead forms in which all syllables linked to the same tone have been affected.

Myers (Reference Myers1997) attributes coalescence at the stem level and tonal alternations at the word level to the Obligatory Contour Principle (OCP; Leben Reference Leben1973, Reference Leben and Fromkin1978, McCarthy Reference McCarthy1986). He assumes a version of the OCP constraint mediated by the syllable (the tone-bearing unit), whose ACC definition is given in (28).

  1. (28)

A syllable-based definition of the OCP constraint is crucial, because Myers (Reference Myers1997: 853–854) assumes, on the basis of the phonological and phonetic inertness of the low tone, that the two surface tones are represented in terms of a privative opposition between the presence (high tone) and absence of tone (low tone). Forms containing two high-toned syllables separated by a phonetically low-toned, and hence phonologically toneless, syllable (where identical tones are adjacent at the tonal tier, but are not associated to adjacent TBUs) are shown to be grammatical, even though they would violate the generalised version of the constraint.

Myers (Reference Myers1997: 870–871) explains the difference in OCP-repair strategies at the stem and word levels by adopting a stratal organisation of the phonological component, in which progressively larger morphological domains are evaluated by grammars with potentially different rankings, with the output of one level of evaluation serving as input to the following level. In his analysis, the constraint ranking responsible for coalescence is restricted to the stem stratum. At the word stratum, the ranking is reversed in such a way that coalescence is no longer the optimal repair strategy for OCP(H) violations, which is why Meeussen's Rule applies instead. I adopt this approach, and additionally assume a ‘clean-up’ operation introduced by Trommer (Reference Trommer2011: 76), which applies between strata, removing any improperly integrated nodes and association lines, and assigning one common morphological colour to all remaining elements.

In the ACC reanalysis of the Shona tonal patterns, the OCP(H) constraint, ranked above Max(H), is responsible for the non-realisation of some input high tones, both as an independent repair at the word level and as a subcomponent of non-reductive coalescence at the stem level. The stem-level spreading subcomponent of coalescence is driven by Specify(σ,T), a phonetic clone of a constraint mandating that syllables be associated to tonal nodes, formulated in (29a).

  1. (29)

To ensure satisfaction by high-tone spreading rather than high-tone epenthesis, Dep(T) has to be ranked higher than *Long(T) in (29b), a markedness constraint against multiply-linked tones. On its own, this ranking predicts that high tones should spread onto all toneless syllables, whether they are underlyingly underspecified or are linked to underlying high tones via association lines that have been made invisible in order to satisfy OCP(H), in violation of Specify(σ,T).Footnote 13 This is not the case. As shown in (30a), high tones in Shona do not spread leftwards onto toneless syllables at all. Rightwards, no spreading applies in nouns and adjectives either, as in (b).Footnote 14

  1. (30)

To restrict spreading to those syllables that dominate delinked tones, Specify(σ,T) has to be outranked by a constraint that can block spreading onto underlyingly toneless syllables. This can be achieved with *σ´ in (31a), the general clone of a constraint penalising high-toned TBUs.

  1. (31)

On this analysis, the spreading subcomponent of non-reductive coalescence displays a type of phonologically derived environment effect (Kiparsky Reference Kiparsky and Fujimura1973, Reference Kiparsky, Hargus and Kaisse1993), whereby a process only applies to structures derived by the application of another process.

The tableau in (32) illustrates the interaction of the relevant constraints with a stem-level evaluation of [sékúru] ‘grandfather’.

  1. (32)

In the faithful candidate, (a), the initial and the second syllable each dominate a separate high tone. This configuration incurs a fatal violation of OCP(H). In candidates (b)–(d), this violation is avoided by delinking one of the offending tones, at the cost of violating Max(H). In (32b), delinking results in the candidate having two TBUs that are not overtly specified for tone. This does not help remove violations of *σ´, since it is a general clone which assesses the entire output structure, where the second TBU is still associated to a high tone. On the other hand, the next constraint in the hierarchy, Specify(σ,T), is a phonetic clone, which only assesses properly integrated material. Consequently, even though the second TBU dominates a covert high tone, this information is not accessible to Specify(σ,T), leading to a second violation and the elimination of the candidate. In (c), the retained tone spreads onto the syllable that has lost its underlying tone. The additional violation of Specify(σ,T) is therefore avoided. Spreading the first high tone onto the underlyingly high-toned following syllable violates *Long(T) and *Contour(T) in (31b), a general clone of a constraint penalising syllables associated to more than one tone, but these constraints are low-ranked, and do not affect the result. The evaluation also includes a candidate, (d), in which the retained high tone spreads even further, onto the underlyingly unspecified final syllable. This removes the last violation of Specify(σ,T), but incurs an additional violation of the higher-ranked *σ´, which results in the elimination of the candidate.

To recapitulate, non-reductive coalescence in Shona can be decomposed into the delinking of all but one of the adjacent high tones associated to neighbouring syllables, driven by a syllable-mediated OCP(H) constraint, accompanied by spreading of the retained tone onto the syllables whose association to underlying tones has been lost. Spreading is driven by Specify(σ,T), and kept in check by a general markedness constraint against high-toned syllables, *σ´, which prevents spreading onto underlyingly underspecified syllables.

At the word level, coalescence is no longer the optimal repair for OCP(H). This can be achieved by ranking *Contour(T), the constraint that militates against spreading onto an underlyingly specified syllable by penalising syllable nodes dominating multiple tonal nodes (covert or overt), above Specify(σ,T). Under this ranking, delinking a high tone becomes the optimal strategy to satisfy OCP(H). If delinking a tone from a single syllable results in the modification of the left edge of a tonal span (understood as a single tone associated to multiple TBUs), the associations linking it to all dominating TBUs are delinked instead, which has the effect of lowering an entire tonal span.

4 Discussion

In this paper, I have shown that a range of alternations that have been labelled as ‘coalescence’ or ‘fusion’ in the literature can be analysed in Autosegmental Coloured Containment Theory without recourse to a dedicated operation replacing two elements of phonological representation with a single one. In addition to accounting for both reductive coalescence, in which two elements (typically segments) are simplified to one that has some features of both input elements, and non-reductive coalescence, in which a sequence of adjacent features is replaced by a single multiply-linked feature, the proposed analysis captures the distinction between two subtypes of reductive coalescence: assimilatory, which results from the interaction of two independently motivated processes of assimilation and spreading, and compensatory, which cannot be so decomposed.

The property of ACC that allows it to account for the opaque interaction of assimilation and deletion is the assumption of containment, which holds that the input is (covertly) present in the output form and can affect its shape. This potentially very powerful principle is kept in check by the Cloning Hypothesis in (13), which limits the influence of covert structures on overt ones to the effect of general clones of markedness constraints, which assess the entire output structure. As shown in §3.3, general clones of positive markedness constraints such as Share can act as opaque drivers, where a spreading process is triggered by covert material, yielding overapplication opacity. A different type of overapplication can result from opaque non-blocking, where a structure penalised by the constraint (e.g. high-toned TBUs in Shona) can only be created when already covertly present. As well as providing an account of overapplication opacity, general markedness constraints have been shown to offer a way to account for underapplication, including chain shifts. For example, Popp (Reference Popp2019) observes that general clones of negative segmental markedness constraints, assigning a violation for a certain combination of features dominated by the same root node, can opaquely block a process spreading one of these features onto a segment that dominates another one, even if the latter has been delinked and is therefore not pronounced, as in (33). Popp utilises this property to analyse partial height harmonies, where underlying mid vowels raise to high but mid vowels derived by raising do not, arguing that raising in one fell swoop is blocked by a general constraint prohibiting [+high, +low] vowels. (‘×’ indicates blocking.)

  1. (33)

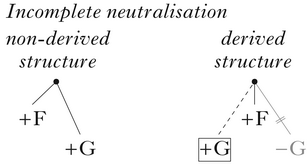
While correspondence-based Optimality Theory, enhanced with some opacity-specific device such as Sympathy Theory (McCarthy Reference McCarthy1999) or targeted constraints (Wilson Reference Wilson2000), is capable of deriving underapplication and overapplication opacity (and hence also the difference between compensatory and assimilatory coalescence), the advantages of the assumption that apparently deleted elements are still present in the output go further. For example, Trommer (Reference Trommer2015: n. 7) observes that general negative markedness constraints can be used to explain ‘grandfather effects’, where a certain structure is tolerated when underlying, but not when created by a phonological process (McCarthy Reference McCarthy2003): they are mute on underlyingly marked structures (so, for example, the constraint used in (33) cannot drive the repair of underlying [+F, +G] segments), but can block the creation of new ones. Furthermore, the assumption of covert structure has been argued to offer a way to analyse incomplete neutralisation, i.e. subtle phonetic differences between segments which belong to the same category in the output, but are derived from different inputs (Port & O'Dell Reference Port and O'Dell1985). As pointed out by van Oostendorp (Reference Oostendorp2008), in Coloured Containment Theory, derived and non-derived segments are represented differently, as in (34). Given a phonetic implementation component sensitive to structures that are not properly integrated, incomplete neutralisation facts can be accounted for.

  1. (34)

Another difference between ACC and correspondence-based OT is their treatment of locality constraints on coalescence. Both frameworks are able to impose a limit on the distance of the fused segment from its underlying source(s), by means of NoSkipping and Linearity constraints respectively. However, only a framework that views coalescence as involving autosegmental spreading can also block long-distance coalescence across segments of a certain quality, using a constraint against line crossing. This has been argued to be necessary by Cain (Reference Cain2000) on the basis of long-distance coalescence in Dhivehi, where hiatus formed across a stem-final high front vowel and a vowel-initial suffix (such as the indefinite suffix /-ek/) is resolved by fusing the former with the vowel in the preceding syllable, creating a diphthong, as in (35a), unless a retroflex segment intervenes, in which case glide insertion applies instead, as in (b).

  1. (35)

Cain explains this pattern by assuming that both retroflexes and front vowels are [+coronal, ―anterior] segments (following Lahiri & Evers Reference Lahiri, Evers, Paradis and Prunet1991) and arguing that the feature [―anterior] from the high front vowel cannot spread across a retroflex consonant, as this would involve crossing of association lines.

The two properties of Autosegmental Coloured Containment Theory mentioned above, i.e. the ability to account for opaque interactions and for the blocking of coalescence across intervening segments, are also found in rule-based autosegmental phonology. Thus the analyses of coalescence patterns proposed in this article could be recast in terms of a sequence of ordered rules of spreading, delinking and node merger. What distinguishes ACC from autosegmental phonology is its treatment of conspiracies. As an optimality-theoretic framework, it has a direct way of characterising the functional unity of various processes in the language, by linking them to a single constraint on the output form. This can be illustrated with tonal processes in Zezuru Shona, where, as shown by Myers (Reference Myers1997), the OCP(H) constraint not only drives three different tonal processes (coalescence, Meeussen's Rule and Tone Slip), but also acts as a blocker, preventing bounded tonal spreading if the syllable following the target one is associated to a H tone, as in (36).

  1. (36)

While a rule-based analysis could describe the tonal patterns of Shona, it could not capture the fact that they all share the common goal of avoiding a marked structure.

5 Summary

Coalescence is a heterogeneous phenomenon, encompassing three different types of alternations. Although lacking a dedicated fusion operation, Autosegmental Coloured Containment Theory is able to account for all three by decomposing them into independently motivated subcomponents: (i) spreading of some autosegmental nodes, and (ii) delinking (or non-linking) of others. In reductive coalescence, two types of constraints can act as the drivers for the spreading subcomponent. In compensatory coalescence, interpreted as a kind of feature stability, the driver is Max[F], which requires the preservation of a certain feature. In assimilatory coalescence, understood as the opaque interaction of assimilation and deletion, the driver is a general Share constraint, capable of triggering spreading from a covert node. In non-reductive coalescence, spreading is driven by a constraint from the Specify family. It is limited to targets that underlyingly dominate an identical feature by means of a general markedness constraint.

The ACC framework combines three properties that allow it to successfully capture the heterogeneity of coalescence processes and their relation to other alternations in a given language. First, as an optimality-theoretic framework, it can explain conspiracies linking coalescence with other processes. Second, its representational assumptions, which it shares with autosegmental phonology, make it possible to express locality restrictions on long-distance coalescence. Finally, the adoption of the principle of containment, and the idea that covert structures can influence the shape of the output, allow it to capture the opacity involved in some coalescence patterns.

Footnotes

I would like to thank three anonymous reviewers, as well as the Phonology editorial team, for their constructive and challenging comments, which have led to considerable improvement of this paper. I am also indebted to Eva Zimmermann, Jochen Trommer, Jelena Stojković, Gereon Müller, Andrew Murphy, Greg Kobele and Eric Baković for helpful discussion at various stages of this work. Finally, I am very grateful to Keith Snider, Andrew Kostakis, Mike Berger and Will Bennett for generously sharing their language expertise and/or otherwise inaccessible sources. This work was carried out as part of the DFG research training group GRK 2011 (Interaction of Grammatical Building Blocks).

1 All representational conventions used in the paper are discussed in §3.1.

2 In the transcriptions in this article, morpheme boundaries are marked with a hyphen; segments that cannot be assigned to a single morpheme due to coalescence are enclosed in «». Glossing abbreviations follow those found in the Leipzig Glossing Rules (Comrie et al. Reference Comrie, Haspelmath and Bickel2015), with the following additions: cl = class, imps = impersonal, mal = malefactive, mvm = main verb marker, rem = remote, term = terminal verb suffix.

3 The fact that the two input segments have been replaced with a single one can be detected auditorily by native speakers of Polish, as the language has a surface contrast between affricates and stop–fricative sequences, exemplified by minimal pairs such as [ɔʦala] ‘saves’ vs. [ɔtsala] ‘desalinates’, and [vʲjɛʧnɨ] ‘eternal’ vs. [vʲjɛtʃnɨ] ‘windy’.

4 I am grateful to an anonymous reviewer for bringing this point to my attention.

5 Although the names ‘colour’ and ‘visibility’ both use a visual metaphor, they are different attributes: colour is a property of all underlying material – both nodes and association lines – and cannot be modified by the phonology, while visibility is exclusively a property of association lines. The phonological component can make an underlying association line invisible.

6 Constraints that have this effect are also known by other names in the Coloured Containment Theory literature, e.g. Parse-σ in van Oostendorp (Reference Oostendorp2007, Reference Oostendorp2008) and PhoneticVisibility (PVis) in Zimmermann (Reference Zimmermann2017). I adopt Max, used in Trommer (Reference Trommer2011, Reference Trommer2014) and Zimmermann (Reference Zimmermann2013), as the most widely recognised name, although it should be borne in mind that the constraint is redefined here as compared to its correspondence-theoretic counterpart.

7 Recall that the phonological component has limited access to the colour, i.e. the morphological affiliation, of nodes and association lines, in that it can distinguish between material with different colours (i.e. belonging to different morphemes) and between coloured (underlying) and colourless (epenthetic) structures.

8 Although tableau (20) does not illustrate this, Max[―high] has to be ranked lower than the driver of deletion, *Hiatus (and also lower than constraints penalising other repairs). This is because segment deletion violates not only Max(•) but also Max[F] constraints for the features dominated by the deleted root node. Ranking Max[―high] above *Hiatus would block deletion in forms in which the hiatus involves two non-high vowels, such as [ɓ-aɓa-fundi] ‘of students’ (cf. [aɓa-fundi] ‘students’), yielding *[ɓa-aɓa-fundi].

9 To prevent reassociation to a vowel (e.g. resulting in [gəforpam] in (24)), it is necessary to employ a more specific NoSkipping constraint, penalising segments intervening between two vowels linked to the same [+round] feature, ranked above the general NoSkipping constraint. This is because reassociation to vocalic segments is allowed in Chaha but only when it is local, as in [fixe-t«o»] ‘one having proliferated’ (used adverbially; proliferate-cvbt-imps), cf. [fixe-tə-w-i] ‘one having proliferated’ (used as a verb; proliferate-cvbt-imps-mvm) (Banksira Reference Banksira2013: 167).

10 A general clone of the *NC̥ constraint as formulated by Pater (Reference Pater, Kager, van der Hulst and Zonneveld1999) would be insufficient to account for the opaque interaction of spreading and deletion. This is because, in the original formulation, the constraint is negative. General clones of negative markedness constraints cannot drive spreading (coupled with the delinking of the offending feature), because, irrespective of whether spreading applies, the marked structure (here, a nasal stop followed by a voiceless obstruent) is still covertly present in the output, causing a violation.

11 To derive the optional pattern in which voicing applies without the concomitant deletion of the nasal, it would be necessary to adopt the assumptions of a stochastic framework, such as Stochastic OT (Boersma Reference Boersma1997, Boersma & Hayes Reference Boersma and Hayes2001) or Noisy Harmonic Grammar (Boersma & Pater Reference Boersma, Pater, McCarthy and Pater2016), which would make it possible to (temporarily) reverse the ranking of Max(•) with respect to *Coda.

12 The high tone in [véreng-a] is not underlying; it is derived by a word-level process of bounded high-tone spreading.

13 If full specification and a H–L distinction were assumed, then the constraints mentioned above (together with a markedness constraint penalising high-toned TBUs ranked lower than an analogous constraint for low tones) would be sufficient to derive the coalescence pattern, as spreading would be correctly limited to those syllables that become unspecified for tone, and hence ill-formed due to their violation of Specify(σ,T).

14 In verbs, the high-tone span does not extend beyond the two-syllable window created by a process of ternary spreading. This will be set aside here.

References

Aoki, Paul K. (1974). An observation of vowel contraction in Xhosa. Studies in African Linguistics 5. 223–241.Google Scholar
Arvaniti, Amalia (1999a). Greek voiced stops: prosody, syllabification, underlying representations or selection of the optimal? In Proceedings of the 3rd International Linguistics Conference for the Greek language. Athens: Ellinika Grammata. 883–890.Google Scholar
Arvaniti, Amalia (1999b). Standard Modern Greek. Journal of the International Phonetic Association 29. 167–172.CrossRefGoogle Scholar
Arvaniti, Amalia & Joseph, Brian D. (2000). Variation in voiced stop prenasalization in Greek. Glossologia 11–12. 131–166.Google Scholar
Awobuluyi, Ọladele (1987). Towards a typology of coalescence. Journal of West African Languages 17. 5–22.Google Scholar
Baković, Eric (2005). Antigemination, assimilation and the determination of identity. Phonology 22. 279–315.CrossRefGoogle Scholar
Baković, Eric (2007). A revised typology of opaque generalisations. Phonology 24. 217–259.CrossRefGoogle Scholar
Baković, Eric (2017). Apparent ‘sufficiently similar’ degemination in Catalan is due to coalescence. Proceedings of the Linguistic Society of America 2. https://doi.org/10.3765/plsa.v2i0.4037.CrossRefGoogle Scholar
Banksira, Degif Petros (2000). Sound mutations: the morphophonology of Chaha. Amsterdam: Benjamins.CrossRefGoogle Scholar
Banksira, Degif Petros (2013). Chaha labialization and palatalization as coalescence. Brill's Annual of Afroasiatic Languages and Linguistics 5. 159–190.CrossRefGoogle Scholar
Blaho, Sylvia, Bye, Patrik & Krämer, Martin (eds.) (2007). Freedom of analysis? Berlin & New York: Mouton de Gruyter.CrossRefGoogle Scholar
Blust, Robert (2004). Austronesian nasal substitution: a survey. Oceanic Linguistics 43. 73–148.CrossRefGoogle Scholar
Boersma, Paul (1997). How we learn variation, optionality, and probability. Proceedings of the Institute of Phonetic Sciences of the University of Amsterdam 21. 43–58.Google Scholar
Boersma, Paul & Hayes, Bruce (2001). Empirical tests of the Gradual Learning Algorithm. LI 32. 45–86.Google Scholar
Boersma, Paul & Pater, Joe (2016). Convergence properties of a Gradual Learning Algorithm for Harmonic Grammar. In McCarthy, John J. & Pater, Joe (eds.) Harmonic Grammar and Harmonic Serialism. London: Equinox. 389–434.Google Scholar
Cain, Bruce D. (2000). An OT account of coalescence and compensatory lengthening in Dhivehi (Maldivian). Working Papers of the Cornell Phonetics Laboratory 13. 1–33.Google Scholar
Casali, Roderic F. (1990). Contextual labialization in Nawuri. Studies in African Linguistics 21. 319–347.Google Scholar
Casali, Roderic F. (1996). Resolving hiatus. PhD dissertation, University of California, Los Angeles.Google Scholar
Casali, Roderic F. (1997). Vowel elision in hiatus contexts: which vowel goes? Lg 73. 493–533.Google Scholar
Causley, Trisha (1997). Identity and featural correspondence: the Athapaskan case. NELS 27. 93–105.Google Scholar
Chomsky, Noam & Halle, Morris (1968). The sound pattern of English. New York: Harper & Row.Google Scholar
Cohn, Abigail (1992). The consequences of dissimilation in Sundanese. Phonology 9. 199–220.CrossRefGoogle Scholar
Comrie, Bernard, Haspelmath, Martin & Bickel, Balthasar (2015). The Leipzig glossing rules. https://www.eva.mpg.de/lingua/resources/glossing-rules.php.Google Scholar
Corbin, Danielle & Plénat, Marc (1992). Note sur l'haplologie des mots construits. Langue française 96. 101–112.CrossRefGoogle Scholar
De Guzman, Videa P. (1978). A case for nonphonological constraints on nasal substitution. Oceanic Linguistics 17. 87–106.CrossRefGoogle Scholar
de Lacy, Paul (2000). Morphological haplology and correspondence. In de Lacy, Paul & Nowak, Anita (eds.) UMOP 24: papers from the 25th reunion. Amherst: GLSA. 51–88.Google Scholar
Goldsmith, John A. (1976). Autosegmental phonology. PhD dissertation, MIT.Google Scholar
Goldsmith, John A. (1984). Meeussen's Rule. In Aronoff, Mark & Oerhle, Richard T. (eds.) Language sound structure. Cambridge, Mass.: MIT Press. 245–259.Google Scholar
Goldsmith, John A. (1990). Autosegmental and metrical phonology. Oxford & Cambridge, Mass.: Blackwell.Google Scholar
Gussmann, Edmund (2007). The phonology of Polish. Oxford: Oxford University Press.Google Scholar
Haas, Wim G. de (1987). An autosegmental approach to vowel coalescence. Lingua 73. 167–199.CrossRefGoogle Scholar
Haas, Wim G. de (1988). A formal theory of vowel coalescence: a case study of Ancient Greek. PhD dissertation, University of Nijmegen.Google Scholar
Halle, Morris & Vergnaud, Jean-Roger (1980). Three dimensional phonology. Journal of Linguistic Research 1. 83–105.Google Scholar
Hayes, Bruce (1986a). Assimilation as spreading in Toba Batak. LI 17. 467–499.Google Scholar
Hayes, Bruce (1986b). Inalterability in CV phonology. Lg 62. 321–351.Google Scholar
Hayes, Bruce (1989). Compensatory lengthening in moraic phonology. LI 20. 253–306.Google Scholar
Herbert, Robert K. (1986). Language universals, markedness theory, and natural phonetic processes. Berlin: Mouton de Gruyter.CrossRefGoogle Scholar
Holton, David, Mackridge, Peter & Philippaki-Warburton, Irene (2004). Greek: an essential grammar of the modern language. London: Routledge.Google Scholar
Hyman, Larry M. (2001). On the limits of phonetic determinism in phonology: *NC revisited. In Hume, Elizabeth & Johnson, Keith (eds.) The role of speech perception in phonology. San Diego: Academic Press. 141–185.Google Scholar
Itô, Junko (1986). Syllable theory in prosodic phonology. PhD dissertation, University of Massachusetts, Amherst. Published 1988, New York: Garland.Google Scholar
Itô, Junko (1989). A prosodic theory of epenthesis. NLLT 7. 217–259.Google Scholar
Kalimeris, Constandinos, Mikros, George & Bakamidis, Stelios (2005). Assimilation and deletion phenomena involving word-final /n/ and word-initial /p, t, k/ in Modern Greek: a codification of the observed variation intended for use in TTS synthesis. Interspeech 2005: Proceedings of the 9th European Conference on Speech Communication and Technology, Lisbon. 2940–2943.Google Scholar
Keer, Edward (1999). Geminates, the OCP and the nature of Con. PhD dissertation, Rutgers University.Google Scholar
Kiparsky, Paul (1971). Historical linguistics. In Dingwall, William Orr (ed.) A survey of linguistic science. College Park: University of Maryland Linguistics Program. 576–642.Google Scholar
Kiparsky, Paul (1973). Abstractness, opacity, and global rules. In Fujimura, Osamu (ed.) Three dimensions in linguistic theory. Tokyo: TEC. 57–86.Google Scholar
Kiparsky, Paul (1985). Some consequences of Lexical Phonology. Phonology Yearbook 2. 85–138.CrossRefGoogle Scholar
Kiparsky, Paul (1993). Blocking in nonderived environments. In Hargus, Sharon & Kaisse, Ellen M. (eds.) Studies in lexical phonology. San Diego: Academic Press. 277–313.CrossRefGoogle Scholar
Lahiri, Aditi & Evers, Vincent (1991). Palatalization and coronality. In Paradis, Carole & Prunet, Jean-François (eds.) The special status of coronals: internal and external evidence. New York: Academic Press. 79–100.CrossRefGoogle Scholar
Lapoliwa, Hans (1981). A generative approach to the phonology of Bahasa Indonesia. Canberra: Australian National University.Google Scholar
Lawrence, Wayne P. (1997). Haplology and vowel underspecification. In Haraguchi, Shosuke (ed.) Report of the special research project for the typological investigation of the languages and cultures of the East and West. Tsukuba: University of Tsukuba. 381–388.Google Scholar
Leben, William R. (1973). Suprasegmental phonology. PhD dissertation, MIT.Google Scholar
Leben, William R. (1978). The representation of tone. In Fromkin, Victoria A. (ed.) Tone: a linguistic survey. New York: Academic Press. 177–219.CrossRefGoogle Scholar
Leben, William R. (1980). A metrical analysis of length. LI 11. 497–509.Google Scholar
McCarthy, John J. (1979). Formal problems in Semitic phonology and morphology. PhD dissertation, MIT.Google Scholar
McCarthy, John J. (1986). OCP effects: gemination and antigemination. LI 17. 207–263.Google Scholar
McCarthy, John J. (1999). Sympathy and phonological opacity. Phonology 16. 331–399.CrossRefGoogle Scholar
McCarthy, John J. (2003). Comparative markedness. Theoretical Linguistics 29. 1–51.CrossRefGoogle Scholar
McCarthy, John J. (2007). Hidden generalizations: phonological opacity in Optimality Theory. Sheffield & Bristol, Conn.: Equinox.Google Scholar
McCarthy, John J. (2010). Autosegmental spreading in Optimality Theory. In Goldsmith, John A., Hume, Elizabeth & Leo Wetzels, W. (eds.) Tones and features: phonetic and phonological perspectives. Berlin & Boston: De Gruyter Mouton. 195–222.Google Scholar
McCarthy, John J., Kimper, Wendell & Mullin, Kevin (2012). Reduplication in Harmonic Serialism. Morphology 22. 173–232.CrossRefGoogle Scholar
McCarthy, John J. & Prince, Alan (1994). The emergence of the unmarked: optimality in prosodic morphology. NELS 24. 333–379.Google Scholar
McCarthy, John J. & Prince, Alan (1995). Faithfulness and reduplicative identity. In Beckman, Jill N., Dickey, Laura Walsh & Urbanczyk, Suzanne (eds.) Papers in Optimality Theory. Amherst: GLSA. 249–384.Google Scholar
Mascaró, Joan (1985). Compensatory diphthongization in Majorcan Catalan. In Wetzels, Leo & Sezer, Engin (eds.) Studies in compensatory lengthening. Dordrecht: Foris. 133–146.Google Scholar
Mini, B. M. & Tshabe, S. L. (eds.) (2003). The greater dictionary of isiXhosa. Vol. 2: K to P. Alice: University of Fort Hare.Google Scholar
Myers, Scott (1987). Tone and the structure of words in Shona. PhD dissertation, University of Massachusetts, Amherst.Google Scholar
Myers, Scott (1997). OCP effects in Optimality Theory. NLLT 15. 847–892.Google Scholar
Oostendorp, Marc van (2003). Comparative markedness and containment. Theoretical Linguistics 29. 65–75.CrossRefGoogle Scholar
Oostendorp, Marc van (2006). A theory of morphosyntactic colours. Ms, Meertens Institute, Amsterdam. Available (December 2020) at https://www.researchgate.net/profile/Marc_Oostendorp.Google Scholar
Oostendorp, Marc van (2007). Derived environment effects and consistency of exponence. In Blaho et al. (2007). 123–148.Google Scholar
Oostendorp, Marc van (2008). Incomplete devoicing in formal phonology. Lingua 118. 1362–1374.CrossRefGoogle Scholar
Pahl, Herbert Walter, Pienaar, A. M. & Ndungane, T. A. (eds.) (1989). The greater dictionary of Xhosa. Vol. 3: Q–Z. Alice: University of Fort Hare.Google Scholar
Pater, Joe (1999). Austronesian nasal substitution and other NC̥ effects. In Kager, René, van der Hulst, Harry & Zonneveld, Wim (eds.) The prosody–morphology interface. Cambridge: Cambridge University Press. 310–343.CrossRefGoogle Scholar
Pater, Joe (2001). Austronesian nasal substitution revisited: what's wrong with NC̥ (and what's not). In Lombardi, Linda (ed.) Segmental phonology in Optimality Theory: constraints and representations. Cambridge: Cambridge University Press. 159–182.CrossRefGoogle Scholar
Popp, Marie-Luise (2019). Why mid vowels are not always mid vowels. NELS 49:3. 39–48.Google Scholar
Port, Robert F. & O'Dell, Michael L. (1985). Neutralization of syllable-final voicing in German. JPh 13. 455–471.Google Scholar
Prince, Alan & Smolensky, Paul (1993). Optimality Theory: constraint interaction in generative grammar. Ms, Rutgers University & University of Colorado, Boulder. Published 2004, Malden, Mass. & Oxford: Blackwell.Google Scholar
Prunet, Jean-François (1986). Spreading and locality domains in phonology. PhD dissertation, McGill University.Google Scholar
Pulleyblank, Douglas (1986). Tone in Lexical Phonology. Dordrecht: Reidel.CrossRefGoogle Scholar
Pulleyblank, Douglas (1989). Nonlinear phonology. Annual Review of Anthropology 18. 203–226.CrossRefGoogle Scholar
Pulleyblank, Douglas (2008). Yoruba vowel patterns: asymmetries through phonological competition. In Bobda, Augustin Simo (ed.) Explorations into language use in Africa. Frankfurt am Main: Peter Lang. 125–157.Google Scholar
Recasens, Daniel (2018). The production of consonant clusters: implications for phonology and sound change. Berlin: Mouton de Gruyter.CrossRefGoogle Scholar
Revithiadou, Anthi (2007). Colored turbid accents and containment: a case study from lexical stress. In Blaho et al. (2007). 149–173.CrossRefGoogle Scholar
Schein, Barry & Steriade, Donca (1986). On geminates. LI 17. 691–744.Google Scholar
Sneddon, James Neil, Adelaar, Alexander, Djenar, Dwi Noverini & Ewing, Michael C. (2010). Indonesian reference grammar. 2nd edn. Crows Nest: Allen & Unwin.Google Scholar
Snider, Keith L. (1989). Vowel coalescence in Chumburung: an autosegmental analysis. Lingua 78. 217–232.CrossRefGoogle Scholar
Snider, Keith L. (2018). Tone analysis for field linguists. Dallas: SIL International.Google Scholar
Stahlke, Herbert F. W. (1976). Segment sequences and segmental fusion. Studies in African Linguistics 7. 41–63.Google Scholar
Steriade, Donca (1982). Greek prosodies and the nature of syllabification. PhD dissertation, MIT.Google Scholar
Stevens, Alan M. & Schmidgall-Tellings, A. Ed. (2010). A comprehensive Indonesian–English dictionary. 2nd edn. Athens, Oh.: Ohio University Press.Google Scholar
Trommer, Jochen (2011). Phonological aspects of Western Nilotic mutation morphology. Habilitationsschrift, University of Leipzig.Google Scholar
Trommer, Jochen (2014). Moraic prefixes and suffixes in Anywa. Lingua 140. 1–34.CrossRefGoogle Scholar
Trommer, Jochen (2015). Moraic affixes and morphological colors in Dinka. LI 46. 77–112.Google Scholar
Trommer, Jochen (2020). The subsegmental structure of German plural allomorphy. NLLT. https://doi.org/10.1007/s11049-020-09479-7.CrossRefGoogle Scholar
Trommer, Jochen & Zimmermann, Eva (2014). Generalised mora affixation and quantity-manipulating morphology. Phonology 31. 463–510.CrossRefGoogle Scholar
Tshabe, S. L. & Shoba, F. M. (eds.) (2006). The greater dictionary of isiXhosa. Vol. 1: A to J. Alice: University of Fort Hare.Google Scholar
Vaux, Bert (1998). The laryngeal specifications of fricatives. LI 29. 497–511.Google Scholar
Wetzels, Leo (1986). Phonological timing in Ancient Greek. In Wetzels, Leo & Sezer, Engin (eds.) Studies in compensatory lengthening. Dordrecht: Foris. 297–344.CrossRefGoogle Scholar
Wetzels, W. Leo (1995). Mid-vowel alternations in the Brazilian Portuguese verb. Phonology 12. 281–304.CrossRefGoogle Scholar
Wheeler, Max W. (2005a). Cluster reduction: deletion or coalescence? Catalan Journal of Linguistics 4. 57–82.CrossRefGoogle Scholar
Wheeler, Max W. (2005b). The phonology of Catalan. Oxford: Oxford University Press.Google Scholar
Wilson, Colin (2000). Targeted constraints: an approach to contextual neutralization in Optimality Theory. PhD dissertation, Johns Hopkins University.Google Scholar
Zimmermann, Eva (2013). Vowel deletion as mora usurpation: the case of Yine. Phonology 30. 125–163.CrossRefGoogle Scholar
Zimmermann, Eva (2017). Morphological length and prosodically defective morphemes. Oxford: Oxford University Press.CrossRefGoogle Scholar