2.1 Stress

Stress is realised as acoustic prominence on one or more syllables in a word. The study of stress is as old as the study of phonology in generative grammar. Because of the wide variety of patterns in the typology of stress, it makes for a lucrative testing ground for formal theories of linguistics. For some previous work that engages large tracts of the stress typology, see Hyman (Reference Hyman1977), Booij (Reference Booij1983), Halle & Vergnaud (Reference Halle and Vergnaud1987), Dresher & Kaye (Reference Dresher and Kaye1990), Bailey (Reference Bailey1995), Hayes (Reference Hayes1995); Gordon (Reference Gordon2002); and Heinz (Reference Heinz2009).

2.2 Finite-state representations of stress

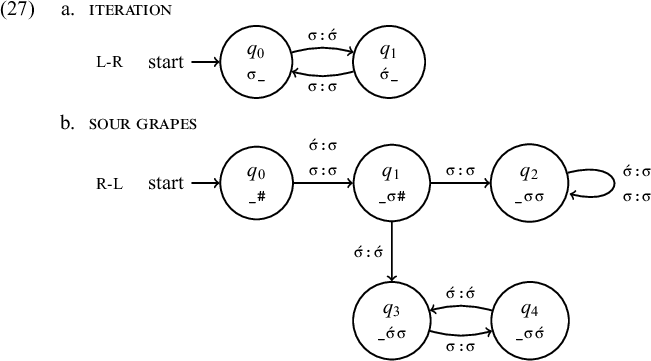
In this article, I study stress as a mapping from an input string of syllables that are unmarked for stress to an output string of syllables that are marked for stress. To study the formal properties of these mappings, I represent them using finite-state transducers (FSTs; Kaplan & Kay Reference Kaplan and Kay1994; Mohri Reference Mohri1997; see Sakarovitch Reference Sakarovitch2006 for an introduction). An FST is a kind of directed graph where a set of states are connected by transitions between those states. FSTs provide a medium to study the abstract computational properties a function has by making it clear what kind of information the function is sensitive to. In this article, the relevant information encoded by a certain state is given as a label appearing on the state. The transitions are labelled with input–output pairs, where the input symbol is given to the left of a colon and the output symbol appears to the right. When moving through a machine, the current state of the transduction encodes information that is relevant to the function it represents. The function represented by (6) deletes an input b that appears immediately after an input a:

When the transduction is in $q_0$ , this indicates either the start of the string, or that the symbol most recently read was a b: all transitions leading to $q_0$ have an input b. Thus, b is the minimal suffix leading to $q_0$ , and so state $q_0$ is labelled b _, indicating that the transducer has just read (if anything) a b, and that it is now ready to read the symbol immediately to the right of that b. State $q_1$ is the ‘a state’: all transitions leading to $q_1$ have an input a, and so it is labelled a _. When in $q_1$ , if the next input symbol is a b, the transition to $q_0$ is taken and the empty string λ is written to the output. This type of transition with λ can be used to model deletion, or when the function needs to wait for more information before deciding what to output for a given input. The transitions leaving $q_0$ and $q_1$ labelled with $\#$ indicate reading of the word boundary and the end of the word. As word boundaries have no phonetic content, they contribute λ to the output. Throughout the article, I exclude these where they are irrelevant – that is, when the word boundary does not affect the behaviour of a particular function. The direction in which the transduction applies is noted with ‘L-R’ or ‘R-L’ under the transducer. This is for clarity for the reader, and is not part of the formal definition of an FST. A transduction that applies left to right starts by reading the symbol at the left edge of the string, and vice versa. The transduction derives the following outputs for the example inputs:

To demonstrate the application of a transduction to a string, consider the following derivation for input (7a). Diagrams such as the one in (8) are helpful in interpreting transducers, and so feature throughout the article. The input and output lines represent the respective input and output strings. The line of states indicates what transition was taken in the machine. For instance, the sequence can be interpreted as starting in state $q_0$ and taking a transition to state $q_1$ , taking the symbol above the arrow as input and outputting the symbol below the arrow. The transducer in (6) reads the string left to right, and so the function starts at the beginning of the word.

Reading the string left to right, the first input symbol is an a, so the transducer outputs a corresponding a and moves to $q_1$ , where it will remain until it encounters a b or the end of the string. The next two symbols are also a, so the transducer remains in $q_1$ . The fourth symbol is a b, which causes the transducer to output λ and return to $q_0$ . The remaining input symbols are all b, and so the transducer remains in $q_0$ until it reaches the end of the string. The input $aaabbb$ is thus mapped to the output $aaabb$ . Note that FSTs such as this one describe not just a single input–output pair, but will map any input to the correct output for a particular pattern.

Studying phonological patterns in this way reveals the abstract computational properties that phonology has. It indicates which patterns are more, less or equally complex in a mathematically defined way. FSTs are thus an invaluable tool in the pursuit of the most restrictive characterisation of linguistic phenomena such as stress. The input–output mappings in (9) exemplify stress assignment according to the Latin pattern in (3):

An FST for Latin is shown in (10):Footnote ⁴

The transducer reads the input string right to left. The final syllable is never stressed, and so it is output faithfully whether it is light or heavy in the transition from $q_0$ to $q_1$ . That syllable weight is irrelevant at this point is reflected in the label _σ on $q_1$ , which indicates that the transducer has just read an input heavy or light syllable. From there, if a light syllable is seen, it is output as unstressed, as stress avoids light penults. Intuitively, this is the information that is encoded in $q_2$ , as indicated in the label: a light penult has just been read in the input. The next syllable – the antepenult – will then be marked as stressed regardless of its weight. Alternatively, going back to $q_1$ , if a heavy penult is encountered instead, it is stressed in the transition from $q_1$ to $q_3$ . Once $q_4$ is reached, all other input symbols are left unchanged, as the end of the three-syllable window has been reached. Interestingly, the state information makes explicit that some QS languages are sensitive to weight in certain positions, rather than the entire word – the penult is the only syllable where weight matters in Latin, for example.

Consider the following derivations for inputs LLL and LHL. This transducer reads the string right to left, and so the function starts at the end of the word:

It should be noted that finite-state analyses of linguistic patterns are not an assertion that the phonological grammar as it is instantiated in the brain is a series of finite-state machines. Rather, FSTs are merely a useful analytical tool for representing phonological functions. This is because the properties of the transducers tell us about the properties of the functions themselves with regard to computational complexity. For the purposes of this article, the most important property is what kind of information determines movement through the states of the transducer. Is it local to the input or output, or is it non-local information? Does it apply in any part of the word or is it tethered to an edge? These different classes of transducers play distinct roles in the theory of iterative stress presented here, and are discussed in detail here.

3.1 EO functions

In this section, I introduce the EO functions, which implement the cleanup functions necessary when iteration of stress alone fails to capture all aspects of an iterative pattern. Intuitively, EO functions are those for which any changes made to the input string only occur in a fixed window at the edge of the word. More formally, in an FST for an EO function, only a finite number of strings can reach a non-identity transition. Therefore, given a string of sufficient length, the transduction always reaches a state where no further changes can be made to the word. The transitions from these states are self-loops that provide identity mappings – the restriction prevents a return to a state with a non-identity transition. In graph-theoretic terms, these properties mean that the largest subgraph of an EO transducer that can reach a non-identity transition is a directed acyclic graph.

Requiring that only a finite number of input sequences can be followed by a change ensures that EO functions can only make alterations to their input in a fixed window at the word edge. Returning to the Latin transducer in (10), for example, L#, H#, LL# and LH# are the only input sequences that can reach a state with a non-identity transition: $q_1$ or $q_2$ . No transitions return to earlier states, as this would permit an in principle unlimited number of changes to apply to an input, eliminating a necessary property of EO functions that ensures their restrictiveness. In (10), arriving in $q_4$ indicates that the necessary span to determine the behaviour of the function has been read. The function does not ‘care’ about any further input symbols – they are always left unchanged.Footnote ⁵ In the EO transducers throughout this article, such states are labelled with the maximal span of input symbols leading to them, making explicit the size of the window that determines the behaviour of the function. For the Latin transducer, $q_4$ is labelled _σσσ, as this three-syllable window at the right word edge is the maximal span needed to determine the correct output of the Latin stress pattern.

The iterative stress patterns that we observe on the surface are conditioned by a number of atomic stress generalisations that are separate from the iteration of stress itself, such as non-finality, clash and lapse. EO functions encode these atomic properties of iterative stress in a straightforward and restrictive manner, as they are always tethered to an edge in attested iterative patterns. In a non-finality function, for example, the only string leading to a non-identity transition is the right word boundary, # (remembering that the function reads the string from right to left). The next input syllable is output as unstressed, and the rest of the word is left unchanged. The behaviour of the function is determined by a small, local window at the word edge. EO functions provide a direct characterisation of this property of stress atoms. Prioritising the word edge is a property of stress patterns in general: single stress patterns (final stress, penultimate stress, etc.) never place stress more than three syllables away from an edge, nor do iterative patterns begin farther from an edge than that (Hyman Reference Hyman1977; Gordon Reference Gordon2002). EO thus provides a testable hypothesis for iterative stress – a substantive claim couched in computational terms that goes beyond categorisation of surface patterns to explain why iterative patterns appear the way that they do.

3.2 OSL functions

Another relevant class of functions is the OSL class (Chandlee Reference Chandlee2014; Chandlee et al. Reference Chandlee, Eyraud and Heinz2015; Chandlee & Heinz Reference Chandlee and Heinz2018). Intuitively, an OSL function is a function that is calculated based entirely on information in the output string. Processes where application of a rule is iterative, such as spreading of a feature, are in general OSL (Chandlee Reference Chandlee2014; Dolatian et al. Reference Dolatian, Koser, Rawski, Strother-Garcia, Bennett, Bibbs, Brinkerhoff, Kaplan, Rich, Rysling, Van Handel and Cavallaro2021). OSL functions are separated into left and right subclasses (L-OSL and R-OSL). L-OSL functions can express different generalisations than R-OSL functions, as they process the string in opposite directions and so describe iterative patterns only in their respective directions. This output centredness is reflected in OSL transducers, where the states in the machine correspond to sequences of symbols read in the output that are relevant to the changes imposed by the function.

An example of an L-OSL function is left-to-right iteration of stress, as found in Murinbata (Street & Mollinjin Reference Street, Mollinjin and Waters1981):

Placement of iterative stress depends on the output string. Intuitively, this is because the next application of stress depends on where it was last placed, and so this information can only be located in the output; the input contains no stresses. The states of an OSL transducer thus correspond to the most recent output:

The transducer outputs the first syllable it encounters with stress, moving to state $q_1$ . The next syllable is output as unstressed, and the transduction moves back to $q_0$ . In other words, the current state in an OSL transducer encodes information about the output string. Reliance on the output is a defining feature of OSL transducers. Formally, a process is called OSL $_k$ if there is some k such that any two strings with the same $k-1$ suffixes in the output string arrive in the same state. The function represented in (14) is thus OSL $_2$ : any string for which the transduction has just output arrives in $q_1$ , and any string for which the transduction has just output arrives in $q_0$ . The process repeats for the remainder of the word, applying stress iteratively:

Any output string ending in will land in $q_0$ , whereas any output string ending in will be in state $q_1$ . This makes the output-oriented nature of OSL functions explicit: the states do not encode any information about input syllables, but all output strings ending in or will land in their respective state. This is seen in (15), where the five-syllable form ends in $q_1$ , whereas the six-syllable form ends in state $q_0$ .

A consequence of this is that OSL transducers cannot have a ‘waiting’ transition between two states in which the empty string λ is written to the output, unlike the transducer in (18), presented below in §3.3. This configuration in a transducer means that there are infinite pairs of strings with the same output suffix that will land in different states – $q_2$ or $q_3$ in (18) – which is an explicit indication that the function itself is not OSL.

OSL functions can generate some iterative stress patterns, but not all. As will be shown below, for stress assignment where iteration is the only factor, an OSL mapping is sufficient. Placement of further stresses in an iterative chain depends on the previous stress in the output – the input of bare syllables is not enough information. However, if there are other stress phenomena in play, such as clash or non-finality, an OSL function alone is insufficient. This is because such patterns require a small amount of lookahead – information other than the most recent output, which is not available to OSL functions. This article proposes that in such cases, the stress map is the composition of an OSL and EO function, where the first handles the iteration of stress and the second accounts for other factors in the pattern. This provides a unified account of iterative stress patterns that is based on properties of their computation.

Alongside the OSL class is the ISL class (Chandlee Reference Chandlee2014; Chandlee & Heinz Reference Chandlee and Heinz2018). The input-centred counterpart of OSL functions, ISL functions are calculated based entirely on information in the input string. The ISL class includes many common phonological processes such as deletion and epenthesis, and so may seem a natural hypothesis for the cleanup functions of iterative stress. However, I demonstrate below that ISL functions do not provide the correct restriction for the cleanup functions in iterative stress maps.

3.3 Subsequential functions

Another relevant class of functions is the subsequential class (Schützenberger Reference Schützenberger1977; Mohri Reference Mohri1997). Subsequential functions are those that are computable deterministically on their input in a single direction. Subsequential functions are more powerful than EO, ISL or OSL functions, but are still important in the study of phonology. They are subregular, have well-understood automata-theoretic and learnability properties and represent an important division in the space of possible functions that includes many phonological patterns and excludes many non-phonological ones (Oncina et al. Reference Oncina, Garcia and Vidal1993; Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013; Chandlee Reference Chandlee2014; Jardine Reference Jardine2016; Luo Reference Luo2017; Payne Reference Payne2017). Though there are notable exceptions (Jardine Reference Jardine2016; Hao & Andersson Reference Hao, Andersson, Nicolai and Cotterell2019; McCollum et al. Reference McCollum, Baković, Mai and Meinhardt2020; Koser & Jardine Reference Koser, Jardine, Baek, Takahashi and Yeung2020b), most phonological processes are subsequential.

An example of a subsequential stress pattern comes from the default to opposite (DTO) languages. These languages stress a right/leftmost heavy syllable, or the first/last syllable in the opposite direction if no heavies are present. Kwakw’ala exhibits a ‘leftmost heavy or right’ (LHOR) pattern (Bach Reference Bach1975; Hayes Reference Hayes1995):

Reading the string left to right, the first heavy syllable encountered is stressed. If no heavy syllables are encountered, the final light syllable is stressed instead. This type of pattern loses the property of locality that is characteristic of EO, ISL or OSL classes. This is because, to determine if any given H or a final L should be stressed, the function must keep track of the lack or presence of heavy syllables for the entire length of the word up to that point (arrows indicate tracking of information through the string):

The transducer in (18) will generate the LHOR stress pattern:

The transduction proceeds left to right. The transition from $q_0$ to $q_1$ takes an input L and ‘waits’ with λ – no output can be written until more input symbols are seen. If the word is light syllables only, the transduction loops in $q_1$ , outputting Ĺ when the word ends, as seen in the exit transition on input #. If at any point a heavy is seen, it is output with stress and the transduction moves to $q_2$ , where no further changes are made. In intuitive terms, being in $q_1$ means that only light syllables have been read, whereas being in $q_2$ means that at least one heavy has been read. Note that this is not local information; LHOR is a long-distance pattern. That the transducer encodes this information about an arbitrary previous number of symbols it has seen makes the function properly subsequential. The following derivations for LLLL and LLHL demonstrate the LHOR mapping:

When evaluating whether any position in the string, light or heavy, should surface with stress, the function depends on information about the – in principle unbounded – sequence of symbols preceding the current one. The loop in $q_1$ allows for an arbitrarily long sequence of L inputs before stress is ultimately applied. State $q_1$ corresponds to only having read input L for the duration of the transduction, whereas $q_2$ corresponds to having seen at least one H somewhere in the string. The pattern cannot be determined locally, and so it is not OSL, ISL or EO.

One property of properly subsequential functions that separates their expressive power from OSL functions is lookahead. Subsequential functions may contain lookahead – the ‘waiting’ as in (18) for some coming input before making a decision on what to output. OSL functions, however, must write a symbol to the output whenever there is a transition from one state to another. They cannot provide lookahead.

As a consequence of this, some patterns that appear local in an intuitive sense require a properly subsequential function to describe. One example is the stress pattern of Pintupi (Hansen & Hansen Reference Hansen and Hansen1969):

Stress iterates left to right starting from the initial syllable and avoids the final syllable. The pattern combines iteration, demonstrated to be OSL below, with the addition of a non-finality requirement. Though this may seem inconsequential in terms of the computation of the pattern, this non-finality requirement necessitates a properly subsequential function because it requires lookahead. In other words, a single-function analysis of Pintupi is not OSL. In the trisyllable, for example, the third syllable is unstressed. However, in the four-syllable form, the third syllable does bear stress. This means that a transducer for the pattern cannot simply alternate between outputting stressed and unstressed syllables, because the same syllable may be output differently if it is final or not. The transducer is shown in (21):

The transducer must wait whenever it takes an odd syllable (other than the first) as its input. This waiting behaviour was also observed for LHOR stress in (18). In order to know what to output for a given odd syllable, the stress function needs to know whether there is another syllable after it. State $q_2$ thus corresponds to an output , but $q_3$ is a waiting state – an ‘odd syllable’ state. It corresponds to some odd-numbered input syllable, and does not correspond to any additional output beyond that encoded in $q_2$ . This means that information other than recent local outputs is needed to compute the function, and so it is not OSL:

An important question, then, is whether or not this properly subsequential characterisation of Pintupi is appropriate. It suggests that the subsequential boundary bisects the typology of iterative stress patterns and that adding a non-finality generalisation to basic iteration of stress somehow makes the pattern ‘long-distance’, like the LHOR pattern. It also implies that any subsequential pattern may appear in the typology of iterative stress. However, it is not the case that any subsequential function is also a possible stress pattern. For example, a pattern that stresses every odd heavy syllable in a word is definable with a subsequential function:

Such a pattern is clearly pathological and should not be included in the predicted typology of stress patterns. To provide a better hypothesis regarding the typology of iterative stress, I argue that patterns like Pintupi are fundamentally local in a way that properly subsequential patterns are not. To make this property of stress computation explicit, it is proposed that the best characterisation of iterative stress is as the composition of an OSL and EO function into a combined map. The apparent need for lookahead in some iterative patterns suggests subsequential functions, but the compositional analysis shows that reference to this level of power is unnecessary: iterative patterns are merely the composition of different stress primitives that are formally local. I demonstrate that the OSL plus EO composed map is a better hypothesis for iterative stress than one that claims subsequential power, as it excludes patterns like (23).

3.4 Function composition

When two functions are composed, the output of the first function becomes the input for the second function. Application of successive rules in a derivational phonological analysis, such as in SPE, is a kind of function composition (Johnson Reference Johnson1972; Kaplan & Kay Reference Kaplan and Kay1994). I argue that iterative stress mappings are best expressed as the composition of one OSL function and some (small) number of EO functions providing ‘cleanup’ that act in place of lookahead to derive the correct output. Thus, the phonological grammar is composed of these individual stress atoms, and the grammar knows which order they must apply in. To demonstrate, consider the pattern of Pintupi in (20). Instead of using a single properly subsequential function as in (21), here it is separated into an OSL function dubbed iteration, which achieves the basic iteration of stress, and an EO function dubbed non-finality, which removes a final stress when one is present. Here and for the remainder of the article, where there are multiple transducers, they apply in the order of their alphabetical label:

The L-OSL function iteration in (24a) applies alternating stress, beginning with the initial syllable. The EO function non-finality in (24b) takes the output of the first function as its input. If the first syllable it encounters is stressed, it removes the stress. Otherwise, it outputs syllables faithfully. Since the first symbol it reads is really the last syllable, this amounts to deletion of stress on a final syllable, encoding the non-finality property of Pintupi. The only input substring that leads to a non-identity transition is the word boundary, # (which implicitly leads to the start state in (24b)), and so non-finality is EO. Reaching $q_1$ indicates that the relevant span of input symbols (one) to calculate the pattern has been seen, and so the only transitions leaving $q_1$ are identity-mapping loops back to $q_1$ .

Examples of how the two functions interact are given here for five- and six-syllable forms. These diagrams should be read top to bottom; note how the output of iteration lines up vertically with and matches the input for non-finality:

iteration and non-finality interact to produce the correct outputs for Pintupi. It is merely the composition of local stress atoms, and requires no reference to a properly subsequential function. This is because, at a fundamental computational level, it is not a long-distance pattern. However, as demonstrated above, a single-function analysis does require use of a properly subsequential function.

The restriction to EO cleanup functions in the composition is a crucial requirement. Composition in general is powerful in that it can result in a mapping that is more expressive than any of its constituent functions. For example, Heinz and Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) show that sour-grapes harmony (Padgett Reference Padgett, Suzuki and Elzinga1995; Wilson Reference Wilson2003) can be derived from the composition of two subsequential functions working in opposite directions, even though sour grapes itself is not subsequential. McCollum et al. (Reference McCollum, Baković, Mai and Meinhardt2020) further demonstrate that restrictions on interaction are necessary to avoid overgeneration in the interaction of subsequential functions.

These effects are in part because of how directionality affects function composition. When composing functions, the directionality has a direct impact on the expressive power of the generalisations the composition can express. This is because the first function can essentially provide unbounded lookahead by marking the string in some way that informs the behaviour of the second function. Thus, adherence to unidirectionality in the functions constrains the complexity. For example, it is known that the composition of two unidirectional subsequential functions cannot produce a combined map that is more expressive than one that a single subsequential function could produce (Elgot & Mezei Reference Elgot and Mezei1965).

However, this is not true of compositions of subsequential functions operating in opposite directions. Heterodirectional subsequential functions can describe the stress map for DTS stress patterns, which are not subsequential (Hao & Andersson Reference Hao, Andersson, Nicolai and Cotterell2019; Koser & Jardine Reference Koser, Jardine, Baek, Takahashi and Yeung2020b). The composition of a left and right OSL function can also describe non-subsequential functions such as the hypothetical sour-grapes stress pattern from (5), repeated in (26):

Stress iterates through the word only if it is of even length. Though parity counting is in general properly regular for stringsets (Heinz Reference Heinz2007b; Rogers et al. Reference Rogers, Heinz, Fero, Hurst, Lambert, Wibel, Morrill and Nederhof2013; Graf Reference Graf2017), such a stress map can be described as the composition of two heterodirectional OSL functions:

(27a) is iteration, like (24a). It reads the string from left to right, placing stress on every other syllable throughout the word starting with the first syllable. (27b) is the sour grapes function, producing the pathological aspect of the combined map. Application of iteration means that words of even length will end in an unstressed syllable, whereas words of odd length will end in a syllable bearing stress. Sour grapes makes explicit use of this markup information. Reading the string right to left, the final syllable is always output as unstressed in the transition to $q_1$ . The next syllable, the penult, gives the second function the crucial information it needs. A stressed penult indicates a string of even length, and so the transduction moves to $q_3$ which, alternating with $q_4$ , faithfully outputs the input unchanged, preserving the stresses. An unstressed penult instead indicates an odd-parity word, and so the transduction moves to $q_2$ , where all stresses are removed. The composition of the two OSL functions correctly derives the pathological stress map:

Though this is a logically possible stress map, it is clearly pathological and is disallowed by the theory of iterative stress adopted here, which only permits OSL plus EO compositions. Only one OSL function is needed to achieve the basic iteration of stress, while the EO cleanup functions encode edge-adjacent stress generalisations that complete each individual pattern. Sour grapes is clearly not EO, as it may delete stresses that occur at any point in the word. Thus, allowing multiple OSL functions is not only unnecessary, it allows the generation of pathological patterns such as sour grapes stress. Adherence to OSL plus EO compositions places important constraints on the predicted typology of iterative patterns, which I conjecture removes not only sour-grapes patterns but pathological properly subsequential patterns as in (23) as well. I now turn to an analysis of various iterative stress patterns.

3.5 Relationships between function classes

The classes of functions described above form a nested hierarchy based on their expressive power, that is, the types of generalisations that functions from each class can describe. EO functions are also ISL, as they are local to the word edge in the input. Some – but not all – EO functions are OSL.Footnote ⁶ Not every OSL or ISL function is EO. For example, any OSL or ISL function that may apply anywhere in the word and is not tied to a word edge is not EO. The difference emerges partially from that fact that OSL and ISL are defined in terms of output and input substrings, whereas EO is defined in terms of finite distance to the word edge. In other words, they are calculated based on distinct intensional requirements, even when the extensional results of the functions are the same.

EO is partially motivated by the fact that reference to OSL and ISL alone does not provide a sufficiently restrictive characterisation of iterative patterns. This is because the cleanup functions necessary for iterative stress maps are both ISL and OSL.Footnote ⁷ For example, a non-finality requirement could be computed input-locally by searching for the substring ‘ ’ (i.e. final stress) in the input. It could also be computed output-locally if the function instead enforces ‘ ’ in the output at the end of the word, whether the input was stressed or not. Thus, a limitation to OSL plus ISL fails to achieve the correct restrictiveness, because the particular cleanup functions in this article are both ISL and OSL. With no further restrictions, this is then an implicit hypothesis that cleanup functions may be OSL in general. In §3.4, I demonstrated that OSL plus EO compositions provide better typological predictions for iterative stress than when OSL is composed with OSL or ISL.

It is not difficult to determine that the class of EO functions does not overlap completely with the OSL or ISL class. The OSL iteration function in (14) is not EO, as it applies stress throughout the entire word. For example, given an input of bare syllables , an EO function can only stipulate the specific location for stress in a bounded window at the word edge (i.e. stress n, stress $n+2$ , stress $n+4$ , etc.) for all cases of stress. Not only is this insufficient to handle words of all lengths in a finite manner, it is not really iteration at all; it is an enumeration of all possible stress locations. Note that this is the same reason that an ISL function cannot describe iterative stress. Similarly, any attempt to use EO to describe an ISL function that may apply anywhere in the word results in an enumeration of the cases as the size of the word grows. In other words, while all EO functions are ISL and some are OSL, their restriction to the word edge means they are not general enough to describe all ISL or OSL patterns. For the cleanup functions in iterative stress maps discussed in this article, this is a desirable property that increases the restrictiveness of the theory while still capturing the target patterns.

4.1 Iteration of stress

4.2 Non-finality

In systems with non-finality, iteration of stress is disrupted by a requirement that the final syllable surface as unstressed. As discussed in §3.3, one QI example is Pintupi (Hansen & Hansen Reference Hansen and Hansen1969), which has the pattern in (20), repeated in (43):

The iteration function alone does not capture the Pintupi pattern. Unlike Murinbata, the pattern requires a small amount of lookahead that is not available to OSL functions. Rather, a transducer for Pintupi as a single function, as in (21), is properly subsequential, because information other than the most recent output or input is required to compute the function.

Though this suggests that iteration of stress in some languages is more complex than in other languages, it was demonstrated that separating the limited lookahead from the iteration of stress by dividing the map into two different functions reveals underlying similarities among iterative patterns and provides a more restrictive theory of stress than allowing the full range of subsequential functions. It preserves the formal notion of locality present in OSL and EO functions but absent in properly subsequential functions. Both Pintupi and Murinbata use the OSL iteration function, whereas Pintupi requires an additional cleanup step that acts in place of lookahead to enforce non-finality. This comes in the form of the EO function that removes a final stress if present, seen in (24).

A QS version of non-finality appears in Wergaia (Hercus Reference Hercus1986; Hyde Reference Hyde, Oostendorp, Ewen, Hume and Rice2011). As shown in (44), stress iterates from left to right, starting with the first syllable. An odd-numbered final syllable will be stressed if it is heavy, as in (44d), but stress avoids light final syllables, as in (44e) and (44f).

Though this binary weight distinction for non-finality sets Wergaia apart from Pintupi in a descriptive sense, the computation of the stress map is of equal complexity. This is because the decision whether to output an odd-numbered light syllable as stressed depends on whether the current position is at the end of the word. Like the single-function analysis for Pintupi, this is not OSL: it is properly subsequential because of the waiting. It is also amenable to the same compositional analysis as Pintupi, separating the iteration of stress from the non-finality requirement:

The L-OSL transducer in (45a) is an iteration function, placing stress on every odd-numbered syllable regardless of weight. This means that, despite the different input and output symbols, the application of the function is identical to the QI iteration function in (24a). The transducer in (45b) is QS non-finality. Just as in the QI non-finality function of Pintupi in (24b), the only input substring leading to a non-identity transition is the word boundary #, and so it is EO. Taking the output of the first function as its input and working from right to left, it removes stress from final light syllables, otherwise outputting the word faithfully and modelling the weight-specific non-finality requirement of Wergaia. This highlights the fact that, despite the different alphabets, the information encoded in the states is identical to that of Pintupi in (24), reinforcing the fact that the computation of the functions in both cases is the same.

Derivations for odd-parity inputs with light and heavy final syllables are shown in (47):

Despite the differences in the surface generalisations of Pintupi and Wergaia, the fundamental properties underlying the calculation of stress in the two languages are identical. This kind of compositional analysis makes the computational properties of different stress phenomena explicit: iteration of stress is OSL and non-finality is EO, regardless of weight-sensitivity.

4.3 Internal lapse

Languages that display an internal lapse can also be analysed compositionally in this way. QI examples include Garawa (Furby Reference Furby, Furby, Hercus and Kilham1974) and Piro (Matteson Reference Matteson1965). To the best of my knowledge, there are no iterative QS internal-lapse counterparts. The pattern of Garawa is as in (48):

The initial syllable is always stressed. Stress iterates right to left from the penult, but avoids the peninitial syllable if a stress there would create a clash. Since iteration in this case must apply R-L, the OSL function will fail to stress the initial syllable and erroneously stress the peninitial syllable in odd-parity forms. This is again due to the lack of lookahead in the OSL function: a fully subsequential function could provide the necessary lookahead, but an OSL function cannot. This means that two EO cleanup steps are necessary, one placing an initial stress where absent, and a second to resolve clashes that the first would produce:

The R-OSL iteration transducer in (49a) iterates stress right to left starting with the penult. Taking the output of the first function as its input and reading the string left to right, the initial stress function in (49b) adds an initial stress if it is absent, but otherwise leaves the string unchanged. Then, the anti-clash function in (49c) resolves any potential clashes this would create in the transition from $q_1$ to $q_2$ . For Garawa, this clash resolution results in the characteristic internal lapse in odd-parity forms. The rest of the string is left unchanged. Both initial stress and anti-clash are EO, as a finite number of strings lead to a state that could apply a change to the input. For initial stress, this is the word boundary #, and for anti-clash, the sole input sequence is # . The following examples demonstrate the effect of the composed mapping:

Even-parity forms, as in (50a), are unchanged by the EO functions: the action of the OSL function alone provides the correct output. Odd-parity forms, as in (50b), have the first two syllables altered by the EO functions, creating an internal lapse. Though Garawa features a pair of EO functions instead of just one as in Pintupi, the generalisations in both languages adhere to the single-OSL restriction with EO cleanup functions acting in place of the lookahead seen in the subsequential transducers. This indicates that along with non-finality, the forces that create internal lapse are also EO when viewed as atomic stress elements. For clarity, the following derivation shown begins after the iteration function in (49a) has already applied:

4.4 Clash

Thus far, the patterns examined have explicitly avoided placing two stresses next to each other. Clash patterns do the opposite, allowing adjacent stresses. A QI example comes from Ojibwe (Kaye Reference Kaye, Piggott and Kaye1973), shown here:

Stress iterates left to right from the peninitial syllable, and the final syllable is always stressed, even if this results in a clash. In odd-parity forms, binary iteration will not add a final stress, and so an EO function does the job instead.

Like Pintupi, this pattern requires bounded lookahead. The decision to stress the third syllable, for example, cannot be made until the next symbol is read. Whereas Pintupi must avoid stressing the final syllable, Ojibwe is required to do so:

Iteration in (53a) iterates stress left to right starting from the peninitial. This is identical to the Garawa transducer in (49a), 5but operating in the opposite direction. The function in (53b), dubbed finality, adds a final stress if one is absent, but otherwise leaves the string unchanged. This is the inverse of the non-finality function seen for Pintupi in (24b). Just like non-finality, the only input substring leading to a non-identity transition is the word boundary #, and so finality is also EO:

Once again, the EO function demonstrates that the lookahead required to describe the pattern as a single subsequential function is unnecessary in a compositional analysis. Above, it was shown that non-finality and lapse creation are EO. Now, clash can be added to this group of EO stress functions. Example derivations for five- and six-syllable words are given in (55):

In QS languages, a clash may occur incidentally when heavy syllables fall next to another stress that resulted from binary iteration, if the language requires all heavy syllables to be stressed. This can be seen for Fijian in (32). Another interesting case is that of Cayuga (Foster Reference Foster1982). In Cayuga, stress iteratively falls on even-numbered syllables counting from the left, with some further requirements. When the penult is even, it receives main stress regardless of weight, as in (56a) and (56b). An odd penult also receives main stress if it is heavy, as in (56c). If the penult is odd and light, however, the antepenult is stressed instead, as in (56d):

Relying not only on weight but on an apparent even/odd parity distinction, the pattern of Cayuga looks on the surface to be more complex than the others discussed to this point. However, it too breaks down into an OSL iteration function and an EO cleanup function. This is partly because the iterative placement of stress provides a pseudo-parity count on the surface in a way that is local, without explicitly tracking the parity of the entire word or a specific syllable:

The L-OSL function in (57a) is another example of binary iteration. It applies stress to every other syllable starting from the peninitial, regardless of weight. The function cayuga stress in (57b) corrects overapplications of stress. When it encounters an unstressed final syllable, this indicates that the penult is even and stressed, and so the transduction moves to $q_1$ where everything is output faithfully. If instead it encounters a stressed final syllable, it removes the stress and moves to $q_2$ . From here, a heavy syllable is stressed, whereas a light syllable is left unchanged, after which the transducer moves to $q_1$ .

Despite some conceptual similarities to the sour grapes function discussed in §3.4, (57b) is EO – the only input substring leading to a non-identity transition is # – whereas the sour grapes function in (27b) is not. Thus, the composed map adheres to the stated single-OSL plus EO restriction:

Derivations for inputs LLLHL and LLLLLL are given in (59):

So far it has been shown that bounded lookahead is a property shared by a wide range of unidirectional iterative patterns in both QI and QS stress. The inability of the OSL stress iteration function to provide any lookahead is made up for by EO cleanup functions that instantiate the phonological properties of clash, lapse, and non-finality in way that is restrictive and captures their limitation to the word edge. Despite the descriptive differences and apparent surface complexity of some of the patterns, the explicit compositional analyses confirm that they all share fundamental OSL-plus-EO computational properties, described here as the atomic properties of stress. While surface differences that appear quite substantial suggest a more disparate typology for stress when taken at face value, the systems are actually of equal complexity.