Article contents
What Price Substitutivity? A Note on Probability Theory
Published online by Cambridge University Press: 01 April 2022
Extract
Teddy Seidenfeld recently claimed that Kolmogorov's probability theory transgresses the Substitutivity Law. Underscoring the seriousness of Seidenfeld's charge, the author shows that (Popper's version of) the law, to wit:
If (∀D)(Pr(B,D) = Pr(C,D)), then Pr(A,B) = Pr(A,C),
follows from just
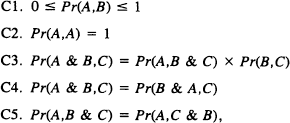
five constraints on Pr of the most elementary and most basic sort.
- Type
- Research Article
- Information
- Copyright
- Copyright © 1981 by the Philosophy of Science Association
Footnotes
The paper was sketched in July 1979 while I served as visiting Professor of Philosophy at Dalhousie University, Halifax; it was completed in the Spring of 1980 while I held a Study Leave from Temple University. Thanks are due to Teddy Seidenfeld, who read the text at each stage and on one major issue set it to rights. Thanks are also due to the referee for his criticisms and advice.
References
- 6
- Cited by


