Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T00:24:41.108Z Has data issue: false hasContentIssue false
  • English
  • Français

The Classical Limit as an Approximation

Published online by Cambridge University Press:  01 January 2022

Benjamin H. Feintzeig
Get access Rights & Permissions [Opens in a new window]

Abstract

I argue that it is possible to give an interpretation of the classical 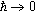ℏ→0 limit of quantum mechanics that results in a partial explanation of the success of classical mechanics. The interpretation is novel in that it allows one to explain the success of the theoretical structure of classical mechanics. This interpretation clarifies the relationship between physical quantities and propositions in quantum theories and provides a precise notion of a quantum theory holding “approximately on certain scales.”

Type
Research Article
Information
Philosophy of Science , Volume 87 , Issue 4 , October 2020 , pp. 612 - 639
Copyright
Copyright © The Philosophy of Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

I would like to thank Samuel Fletcher, Jeremy Butterfield, Neil Dewar, Adam Koberinski, Klaas Landsman, Michael Miller, Kasia Rejzner, and James Weatherall for helpful discussions on these topics. Furthermore, I am indebted to the anonymous referees for greatly improving the quality of this article.

References

Arageorgis, A. 1995. Fields, Particles, and Curvature: Foundations and Philosophical Aspects of Quantum Field Theory in Curved Spacetime. PhD diss., University of Pittsburgh.Google Scholar
Batterman, R. 1991. “Chaos, Quantization, and the Correspondence Principle.” Synthese 89 (2): 189–227..CrossRefGoogle Scholar
Batterman, R.. 2002. The Devil in the Details: Asymptotic Reasoning in Explanation, Reduction, and Emergence. Oxford: Oxford University Press.Google Scholar
Binz, E., Honegger, R., and Rieckers, A.. 2004a. “Construction and Uniqueness of the C*-Weyl Algebra over a General Pre-symplectic Space.” Journal of Mathematical Physics 45 (7): 2885–907..CrossRefGoogle Scholar
Binz, E., Honegger, R., and Rieckers, A.. 2004b. “Field-Theoretic Weyl Quantization as a Strict and Continuous Deformation Quantization.” Annales de l’Institut Henri Poincaré 5:327–46.Google Scholar
Bratteli, O., and Robinson, D.. 1987. Operator Algebras and Quantum Statistical Mechanics. vol. 1. New York: Springer.CrossRefGoogle Scholar
Clifton, R., and Halvorson, H.. 2001. “Are Rindler Quanta Real? Inequivalent Particle Concepts in Quantum Field Theory.” British Journal for the Philosophy of Science 52:417–70.CrossRefGoogle Scholar
Emch, G. 1983. “Geometric Dequantization and the Correspondence Problem.” International Journal of Theoretical Physics 22 (5): 397–420..CrossRefGoogle Scholar
Feintzeig, B. 2015. “On Broken Symmetries and Classical Systems.” Studies in History and Philosophy of Modern Physics B 52:267–73.Google Scholar
Feintzeig, B.. 2017. “On Theory Construction in Physics: Continuity from Classical to Quantum.” Erkenntnis 82 (6): 1195–210..CrossRefGoogle Scholar
Feintzeig, B.. 2018a. “The Classical Limit of a State on the Weyl Algebra.” Journal of Mathematical Physics 59 (11): 112102.CrossRefGoogle Scholar
Feintzeig, B.. 2018b. “On the Choice of Algebra for Quantization.” Philosophy of Science 85 (1): 102–25..CrossRefGoogle Scholar
Feintzeig, B.. 2018c. “Toward an Understanding of Parochial Observables.” British Journal for the Philosophy of Science 69 (1): 161–91..CrossRefGoogle Scholar
Feintzeig, B., Manchak, J., Rosenstock, S., and Weatherall, J.. 2019. “Why Be Regular?” Pt. 1. Studies in History and Philosophy of Modern Physics 65:122–32.Google Scholar
Feintzeig, B., and Weatherall, J.. 2019. “Why Be Regular?” Pt. 2. Studies in History and Philosophy of Modern Physics 65:133–44.Google Scholar
Fletcher, S. 2019. “On the Reduction of General Relativity to Newtonian Gravitation.” Studies in History and Philosophy of Modern Physics 68:1–15.CrossRefGoogle Scholar
Fletcher, S.. 2020. “On Representational Capacities, with an Application to General Relativity.” In “Hole Argument.” Special issue, Foundations of Physics 50:228–49.CrossRefGoogle Scholar
Fraser, D. 2019. “The Development of Renormalization Group Methods for Particle Physics: Formal Analogies between Classical Statistical Mechanics and Quantum Field Theory.” Synthese, forthcoming. https://doi.org/10.1007/s11229-018-1862-0.CrossRefGoogle Scholar
Gamow, G. 1993. Mr. Tompkins in Paperback. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Kadison, R., and Ringrose, J.. 1997. Fundamentals of the Theory of Operator Algebras. Providence, RI: American Mathematical Society.Google Scholar
Landsman, N. P. 1998. Mathematical Topics between Classical and Quantum Mechanics. New York: Springer.CrossRefGoogle Scholar
Landsman, N. P.. 2007. “Between Classical and Quantum.” In Handbook of the Philosophy of Physics, Vol. 1, ed. Butterfield, J. and Earman, J., 417–553. New York: Elsevier.CrossRefGoogle Scholar
Landsman, N. P.. 2017. Foundations of Quantum Theory: From Classical Concepts to Operator Algebras. New York: Springer.CrossRefGoogle Scholar
Lupher, T. 2008. “The Philosophical Significance of Unitarily Inequivalent Representations in Quantum Field Theory.” PhD diss., University of Texas.Google Scholar
Manuceau, J., Sirugue, M., Testard, D., and Verbeure, A.. 1974. “The Smallest C*-Algebra for the Canonical Commutation Relations.” Communications in Mathematical Physics 32:231–43.Google Scholar
Nagel, E. 1998. “Issues in the Logic of Reductive Explanations.” In Philosophy of Science: The Central Issues, ed. Curd, M. and Cover, J., 905–21. New York: Norton.Google Scholar
Nickles, T. 1973. “Two Concepts of Intertheoretic Reduction.” Journal of Philosophy 70:181–201.CrossRefGoogle Scholar
Petz, D. 1990. An Invitation to the Algebra of Canonical Commutation Relations. Leuven: Leuven University Press.Google Scholar
Post, H. 1971. “Correspondence, Invariance, and Heuristics: In Praise of Conservative Induction.” Studies in History and Philosophy of Modern Science 2 (3): 213–55..Google Scholar
Primas, H. 1998. “Emergence in Exact Natural Sciences.” Acta Polytechnica Scandinavica 91:83–98.Google Scholar
Radder, H. 1991. “Heuristics and the Generalized Correspondence Principle.” British Journal for the Philosophy of Science 42 (2): 195–226..CrossRefGoogle Scholar
Reed, M., and Simon, B.. 1980. Functional Analysis. New York: Academic Press.Google Scholar
Rieffel, M. 1989. “Deformation Quantization of Heisenberg Manifolds.” Communications in Mathematical Physics 122:531–62.CrossRefGoogle Scholar
Rieffel, M.. 1993. Deformation Quantization for Actions of ℝd. Memoirs of the American Mathematical Society 506. Providence, RI: American Mathematical Society.Google Scholar
Rieffel, M.. 1994. “Quantization and C*-Algebras.” Contemporary Mathematics 167:67–97.Google Scholar
Rohrlich, F. 1989. “The Logic of Reduction: The Case of Gravitation.” Foundations of Physics 19 (10): 1151–70..CrossRefGoogle Scholar
Rohrlich, F.. 1990. “There Is Good Physics in Theory Reduction.” Foundations of Physics 20 (11): 1399–412..CrossRefGoogle Scholar
Rohrlich, F.. 2002. “The Validity Limits of Physical Theories: Response to the Preceding Letter.” Physics Letters A 295:320–22.Google Scholar
Rosaler, J. 2015a. “‘Formal’ versus ‘Empirical’ Approaches to Quantum-Classical Reduction.” Topoi 34 (2): 325–38..CrossRefGoogle Scholar
Rosaler, J.. 2015b. “Local Reduction in Physics.” Studies in History and Philosophy of Modern Physics 50:54–69.CrossRefGoogle Scholar
Rosaler, J.. 2016. “Interpretation Neutrality in the Classical Domain of Quantum Theory.” Studies in History and Philosophy of Modern Physics 53:54–72.CrossRefGoogle Scholar
Rosaler, J.. 2018. “Generalized Ehrenfest Relations, Deformation Quantization, and the Geometry of Inter-model Reduction.” Foundations of Physics 48:355–85.CrossRefGoogle Scholar
Rosaler, J., and Harlander, R.. 2019. “Naturalness, Wilsonian Renormalization, and ‘Fundamental Parameters’ in Quantum Field Theory.” Studies in History and Philosophy of Modern Physics 66:118–34.CrossRefGoogle Scholar
Ruetsche, L. 2011. Interpreting Quantum Theories. New York: Oxford University Press.CrossRefGoogle Scholar
Scheibe, E. 1973. The Logical Analysis of Quantum Mechanics. Oxford: Pergamon.Google Scholar
Scheibe, E.. 1986. “The Comparison of Scientific Theories.” Interdisciplinary Science Reviews 11 (2): 148–52..CrossRefGoogle Scholar
Waldmann, S. 2015. “Recent Developments in Deformation Quantization.” Contribution to the proceedings of the 2014 Regensburg Conference on Quantum Mathematical Physics. https://arxiv.org/abs/1502.00097v1.Google Scholar
Weatherall, J. 2018. “Regarding the ‘Hole Argument.’” British Journal for Philosophy of Science 69 (2): 329–50..CrossRefGoogle Scholar