Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Arthmar, Rogério
and
Brady, Michael Emmett
2010.
An Analysis that Answers F.Y.Edgeworth's Question, Put to the Logicians and Philosophers Who Read the Journal <i>Mind</i>, Concerning the Importance of Evaluating the Role Played by Keynes's Conventional Coefficient of Risk and Weight, C, in Decision Making.
SSRN Electronic Journal,
Brady, Michael Emmett
2010.
A Comparison-Contrast of Adam Smith, JM Keynes and Jeremy Bentham on Probability, Risk, Uncertainty, Optimism-Pessimism and Decision Making with Applications Concerning Banking, Insurance and Speculation.
SSRN Electronic Journal,
Brady, Michael Emmett
2010.
How to Use Keynes’s Conventional Coefficient of Risk and Weight, c, to Clear Up Misunderstandings and Confusions About Keynes’s Views on the Use on His Principle of Indifference Versus the Use of Laplace’s Principle of Nonsufficient Reason.
SSRN Electronic Journal,
Brady, Michael Emmett
2012.
John Maynard Keynes’s Upper and Lower Valued Probabilities: A Study of How Statisticians, Philosophers, Logicians, Historians, and Economists Failed to Comprehend Keynes’s Breakthrough Application of G.Boole’s Interval Approach to Probability in the 20th Century.
SSRN Electronic Journal,
Bickel, David R.
2012.
Coherent Frequentism: A Decision Theory Based on Confidence Sets.
Communications in Statistics - Theory and Methods,
Vol. 41,
Issue. 8,
p.
1478.
Brady, Michael Emmett
2013.
Adam Smith's Theory of Probability and the Roles of Risk and Uncertainty in Economic Decision Making.
SSRN Electronic Journal,
Brady, Michael Emmett
2014.
Indeterminate Probabilities and Smithian and Keynesian Uncertainty.
SSRN Electronic Journal,
Brady, Michael Emmett
2014.
Adam Smith on Uncertainty, Degrees of Uncertainty and Public Policy Impacts.
SSRN Electronic Journal,
Brady, Michael Emmett
2014.
How Is It Possible for Keynes's Theory of Logical Probability to Be 'Non-Probabilistic'? Answer. Only If You Have Been Confused by Reading Frank P. Ramsey's Reviews of Keynes's <i>A Treatise on Probability</i>.
SSRN Electronic Journal,
Brady, Michael Emmett
2014.
Interval Probabilities, and Not Ordinal Probabilities, are the Foundation of J M Keynes's Approach to Probability.
SSRN Electronic Journal,
Brady, Michael Emmett
2014.
Adam Smith's Definition of Uncertainty and His Application of His Uncertainty Concept in Part I, Chapter XI of the Wealth of Nations.
SSRN Electronic Journal,
Brady, Michael Emmett
2014.
From Adam Smith to John Maynard Keynes and Back to Adam Smith: The Circle Closes. The Old Economic Thinking of Smith and Keynes Combined is Still Superior to Any "New Economic Thinking".
SSRN Electronic Journal,
Brady, Michael Emmett
2014.
A Study of Ramsey's Extremely Poor Reading of Chapter III of J. M. Keynes's A Treatise on Probability and the Refutations Made by J. M. Keynes and Bertrand Russell.
SSRN Electronic Journal ,
Masterton, George
2015.
Equivocation for the Objective Bayesian.
Erkenntnis,
Vol. 80,
Issue. 2,
p.
403.
Brady, Michael Emmett
2016.
J M Keynes's Logical Theory of Probability Is Based on Interval Valued Probability, Not Ordinal Probability: How the Keynesian Fundamentalists Runde, Skidelsky, Carabelli, OODonnell, Meeks Got It All Wrong.
SSRN Electronic Journal ,
Brady, Michael Emmett
2016.
A Rationale Supporting a Decision by Pope Francis and the Arch Bishop of Canterbury to Remove All Economic Advisors from Any Advisory Role Concerning Church Proclamations on Income Inequality, Unemployment and Social Justice: 'Economics' is Not a Positive Science, But an Ethical System Based on Benthamite Utilitarianism.
SSRN Electronic Journal ,
Brady, Michael Emmett
2017.
A Comparison Contrast of the Technical Understanding Exhibited by F.Y. Edgeworth in His Two 1922 Book Reviews of J. M. Keynes's a Treatise on Probability with that of the Keynesian Fundamentalists, Such As Runde, Skidelsky, OODonnell, Carabelli, Feduzi and Lawson, between 1980 and 2016 A Problem of Lost Knowledge.
SSRN Electronic Journal,
Brady, Michael Emmett
2017.
What Emile Borel, the Great, Famous, French Mathematician, Missed by Skipping Part II of the a Treatise on Probability in His 1924 Review of that Book: The Impact of the Ignorance of Part II of the a Treatise on Probability on Modern Assessments of J M Keynes's Logical Theory of Probability.
SSRN Electronic Journal,
Brady, Michael Emmett
2017.
On J M Keynes's Clear Cut Discussion of Interval Valued Probability in Chapter III of the a Treatise on Probability.
SSRN Electronic Journal ,
Brady, Michael Emmett
2017.
A Guide to Help Prepare Readers for J M Keynes's A Treatise on Probability (1921).
SSRN Electronic Journal ,
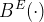 $B^{E}(\cdot) $
should be
$B^{E}(\cdot) $
should be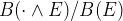 $B(\cdot \wedge E) / B(E) $
. Probability is also important in classical statistics, where it is generally supposed that probabilities are frequencies, and that inference proceeds by controlling error and not by conditioning. I will focus on the tension between these two approaches to probability, and in the main part of the paper show where and when Bayesian conditioning conflicts with error based statistics and how to resolve these conflicts.
$B(\cdot \wedge E) / B(E) $
. Probability is also important in classical statistics, where it is generally supposed that probabilities are frequencies, and that inference proceeds by controlling error and not by conditioning. I will focus on the tension between these two approaches to probability, and in the main part of the paper show where and when Bayesian conditioning conflicts with error based statistics and how to resolve these conflicts.