Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T00:58:10.842Z Has data issue: false hasContentIssue false
  • English
  • Français

Severity and Trustworthy Evidence: Foundational Problems versus Misuses of Frequentist Testing

Published online by Cambridge University Press:  10 February 2022

Aris Spanos
Aris Spanos*
Affiliation:
Virginia Tech, Blacksburg, VA, USA
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For model-based frequentist statistics, based on a parametric statistical model 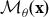${{\cal M}_\theta }({\bf{x}})$ , the trustworthiness of the ensuing evidence depends crucially on (i) the validity of the probabilistic assumptions comprising ${{\cal M}_\theta }({\bf{x}})$ , (ii) the optimality of the inference procedures employed, and (iii) the adequateness of the sample size (n) to learn from data by securing (i)–(ii). It is argued that the criticism of the postdata severity evaluation of testing results based on a small n by Rochefort-Maranda (2020) is meritless because it conflates [a] misuses of testing with [b] genuine foundational problems. Interrogating this criticism reveals several misconceptions about trustworthy evidence and estimation-based effect sizes, which are uncritically embraced by the replication crisis literature.

Type
Article
Information
Philosophy of Science , Volume 89 , Issue 2 , April 2022 , pp. 378 - 397
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of the Philosophy of Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Thanks are due to two anonymous reviewers for many valuable comments and suggestions that helped to improve the discussion significantly.

References

Berkson, Joseph. 1938. “Some Difficulties of Interpretation Encountered in the Application of the Chi-Square Test.” Journal of the American Statistical Association 33:526–36.CrossRefGoogle Scholar
Cohen, Jacob. 1988. Statistical Power Analysis for the Behavioral Sciences (2nd ed.). NJ: Lawrence Erlbaum.Google Scholar
Devroye, Luc. 1986. Non-Uniform Random Variate Generation. NY: Springer.CrossRefGoogle Scholar
Fisher, Ronald A. 1922. “On the Mathematical Foundations of Theoretical Statistics.” Philosophical Transactions of the Royal Society A 222:309–68.Google Scholar
Fisher, Ronald A. 1925. “Theory of Statistical Estimation.” Mathematical Proceedings of the Cambridge Philosophical Society 22(5):700–25.CrossRefGoogle Scholar
Gigerenzer, Gerd. 1993. “The Superego, the Ego, and the Id in Statistical Reasoning.” A Handbook for Data Analysis in the Behavioral Sciences: Methodological Issues, 311–39.Google Scholar
Hacking, Ian. 1965. Logic of Statistical Inference. Cambridge: Cambridge University Press.Google Scholar
Hald, Anders. 2007. A History of Parametric Statistical Inference from Bernoulli to Fisher, 1713–1935. New York: Springer.Google Scholar
Ioannidis, John P. A. 2005. “Why Most Published Research Findings Are False.” PLoS Medicine 2:e124.CrossRefGoogle ScholarPubMed
Lehmann, E. L., and Romano, Joseph P.. 2005. Testing Statistical Hypotheses. New York: Springer.Google Scholar
Mayo, Deborah G. 1996. Error and the Growth of Experimental Knowledge. Chicago: The University of Chicago Press.CrossRefGoogle Scholar
Mayo, Deborah G. 2018. Statistical Inference as Severe Testing: How to Get Beyond the Statistical Wars. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Mayo, Deborah G., and Spanos, Aris. 2004. “Methodology in Practice: Statistical Misspecification Testing.” Philosophy of Science 71:1007–25.CrossRefGoogle Scholar
Mayo, Deborah G., and Spanos, Aris. 2006. “Severe Testing as a Basic Concept in a Neyman-Pearson Philosophy of Induction.” The British Journal for the Philosophy of Science 57:323–57.CrossRefGoogle Scholar
Mayo, Deborah G., and Spanos, Aris. 2011. “Error Statistics.” In Handbook of Philosophy of Science, vol. 7: Philosophy of Statistics, ed. Gabbay, D., Thagard, P., and Woods, J., 151–96. Elsevier.Google Scholar
Neyman, J. 1937. “Outline of a Theory of Statistical Estimation based on the Classical Theory of Probability.” Philosophical Transactions of the Royal Statistical Society of London, A 236:333–80.Google Scholar
Neyman, Jerzy. 1952. Lectures and Conferences on Mathematical Statistics and Probability, 2nd ed. Washington, D. C.: U.S. Department of Agriculture.Google Scholar
Neyman, Jerzy, and Pearson, Egon S.. 1933. “On the Problem of the Most Efficient Tests of Statistical Hypotheses.” Philosophical Transactions of the Royal Society, A 231:289–337.Google Scholar
Pratt, John W. 1961. “Book Review: Testing Statistical Hypotheses, by E. L. Lehmann.” Journal of the American Statistical Association 56:163–67.CrossRefGoogle Scholar
Rochefort-Maranda, Guillaume. 2020. “Inflated Effect Sizes and Underpowered Tests: How the Severity Measure of Evidence Is Affected by the Winner’s Curse.” Philosophical Studies https://doi.org/10.1007/s11098-020-01424-z Google Scholar
Spanos, Aris. 1986. Statistical Foundations of Econometric Modelling. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Spanos, Aris. 2006. “Where Do Statistical Models Come from? Revisiting the Problem of Specification.” In Optimality: The Second Erich L. Lehmann Symposium, ed. Rojo, J., Lecture Notes-Monograph Series, vol. 49, Institute of Mathematical Statistics. OH, Beachwood.Google Scholar
Spanos, Aris. 2010. “Akaike-type Criteria and the Reliability of Inference: Model Selectionvs. Statistical Model Specification.” Journal of Econometrics 158:204–20.CrossRefGoogle Scholar
Spanos, Aris. 2013a. “A Frequentist Interpretation of Probability for Model-Based Inductive Inference.” Synthese 190:1555–85.CrossRefGoogle Scholar
Spanos, Aris. 2013b. “Who Should Be Afraid of the Jeffreys-Lindley Paradox?” Philosophy of Science 80:73–93.CrossRefGoogle Scholar
Spanos, Aris. 2014. “Recurring Controversies about P values and Confidence Intervals Revisited.” Ecology 95 (3):645–51.CrossRefGoogle ScholarPubMed
Spanos, Aris. 2018. “Mis-Specification Testing in Retrospect.” Journal of Economic Surveys 32:541–77.CrossRefGoogle Scholar
Spanos, Aris. 2019. Introduction to Probability Theory and Statistical Inference: Empirical Modeling with Observational Data, 2nd ed. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Spanos, Aris, and McGuirk, Anya. 2001. “The Model Specification Problem from a Probabilistic Reduction Perspective.” Journal of the American Agricultural Association 83:1168–76.Google Scholar
Yule, George U. 1916. An Introduction to the Theory of Statistics, 3rd ed. London: Griffin.Google Scholar
Yule, George U. 1926. “Why Do We Sometimes Get Nonsense Correlations between Time Series: A Study in Sampling and the Nature of Time Series. ” Journal of the Royal Statistical Society 89:1–64.CrossRefGoogle Scholar