Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T00:13:24.860Z Has data issue: false hasContentIssue false
  • English
  • Français

A Fourier Companion Matrix (Multiplication Matrix) with Real-Valued Elements: Finding the Roots of a Trigonometric Polynomial by Matrix Eigensolving

Published online by Cambridge University Press:  28 May 2015

John P. Boyd
John P. Boyd*
Affiliation:
Department of Atmospheric, Oceanic & Space Science, University of Michigan, 2455 Hayward Avenue, Ann Arbor MI 48109, USA
*
*Corresponding author.Email address:[email protected]
Get access

Abstract

We show that the zeros of a trigonometric polynomial of degree N with the usual (2N + 1) terms can be calculated by computing the eigenvalues of a matrix of dimension 2N with real-valued elements Mjk. This matrix 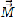is a multiplication matrix in the sense that, after first defining a vector 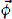whose elements are the first 2N basis functions, 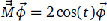. This relationship is the eigenproblem; the zeros tk are the arccosine function of λk/2 where the λk are the eigenvalues of 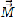. We dub this the “Fourier Division Companion Matrix”, or FDCM for short, because it is derived using trigonometric polynomial division. We show through examples that the algorithm computes both real and complex-valued roots, even double roots, to near machine precision accuracy.

Keywords

65H9965T4042A85Fourier seriestrigonometric polynomialrootfindingsecularcompanion matrix
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 6 , Issue 4 , November 2013 , pp. 586 - 599
Copyright
Copyright © Global Science Press Limited 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Angelova, E. D. and Semerdzhiev, K. I., Methods for the simultaneous approximate derivation of the roots of algebraic, trigonometric and exponential equations, U.S.S.R. Comput. Maths. Math. Phys., 22 (1982), pp. 226–232.CrossRefGoogle Scholar
[2]Boyd, J. P., Computing the zeros, maxima and inflection points of Chebyshev, Legendre and Fourier series: Solving transcendental equations by spectral interpolation and polynomial rootfinding, J. Eng. Math., 56 (2006), pp. 203–219.Google Scholar
[3]Boyd, J. P., Computing the zeros of a Fourier series or a Chebyshev series or general orthogonal polynomial series with parity symmetries, Comput. Math. Appl., 54 (2007), pp. 336–349.CrossRefGoogle Scholar
[4]Boyd, J. P., A comparison of companion matrix methods to find roots of a trigonometric polynomial, J. Comput. Phys., 246 (2013), pp. 96–112.CrossRefGoogle Scholar
[5]Boyd, J. P., Finding the zeros of a univariate equation: Proxy rootfinders, Chebyshev interpolation and the companion matrix, SIAM Rev., 55 (2013), in proof.CrossRefGoogle Scholar
[6]Boyd, J. P. and Sadiq, B. A., Computing the real roots of a Fourier series-plus-linear-polynomial: A Chebyshev companion matrix approach, Appl. Math. Comput., 219 (2012), pp. 819–826.Google Scholar
[7]Carstensen, C., A note on simultaneous rootfinding for algebraic, exponential, and trigonometric polynomials, Comput. Math. Appl., 27 (1994), pp. 7–14.CrossRefGoogle Scholar
[8]Carstensen, C. and Petkovi’c, M. S., On some interval methods for algebraic, exponential and trigonometric polynomials, Computing, 51 (1993), pp. 313–326.CrossRefGoogle Scholar
[9]Carstensen, C. and Reinders, M., On a class of higher order methods for simultaneous rootfind-ing of generalized polynomials, Numer. Math., 64 (1993), pp. 69–84.CrossRefGoogle Scholar
[10]Corless, R. M., Generalized companion matrices in the Lagrange basis, in Proceedings EACA, Gonzalez-Vega, L. and Recio, T., eds., 2004, pp. 317–322.Google Scholar
[11]Corless, R. M., On a generalized companion matrix pencil for matrix polynomials expressed in the Lagrange basis, in Symbolic-Numeric Computation, Wang, D. and Zhi, L.-H., eds., Trends in Mathematics, Natl Nat Sci Fdn China, Birkhäuser Basel, 2007, pp. 1–15.Google Scholar
[12]Corless, R. M. and Litt, G., Generalized companion matrices for polynomials not expressed in monomial bases, unpublished, University of Western Ontario, 2000. Available on Corless’ web site.Google Scholar
[13]Frommer, A., A unified approach to methods for the simultaneous computation of all zeros of generalized polynomials, Num. Math., 54 (1988), pp. 105–116.CrossRefGoogle Scholar
[14]Makrelov, I. V. and Semerdzhiev, H. I., Methods for the simultaneous determination of all zeros algebraic, trigonometric and exponential equations, U. S. S. R. Comput. Maths. Math. Phys., 24 (1984), pp. 99–105.CrossRefGoogle Scholar
[15]Makrelov, I. V. and Semerdzhiev, K. I., On the convergence of two methods for the simultaneous find of all roots of exponential equations, IMA J. Numer. Anal., 5 (1985), pp. 191–200.CrossRefGoogle Scholar
[16]Schweikard, A., Trigonometric polynomials with simple roots, Information Processing Lett., 39 (1991), pp. 231–236.CrossRefGoogle Scholar
[17]Schweikard, A., Real zero isolation for trigonometric polynomials, ACM Trans. Math. Software, 18 (1992), pp. 350–359.CrossRefGoogle Scholar
[18]Weidner, P., The Durand-Kerner method for trigonometric and exponential polynomials, Comput., 40 (1988), pp. 175–179.CrossRefGoogle Scholar