Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T19:24:28.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact Singularity Subtraction from Boundary Integral Equations in Modeling Vesicles and Red Blood Cells

Published online by Cambridge University Press:  09 August 2018

Alexander Farutin  and
Chaouqi Misbah
Alexander Farutin*
Affiliation:
Université Grenoble I/CNRS, Laboratoire Interdisciplinaire de Physique/UMR5588, Grenoble F-38041, France.
Chaouqi Misbah*
Affiliation:
Université Grenoble I/CNRS, Laboratoire Interdisciplinaire de Physique/UMR5588, Grenoble F-38041, France.
*
Email address:[email protected]
*Corresponding author.Email:[email protected]
Get access

Abstract

The study of vesicles, capsules and red blood cells (RBCs) under flow is a field of active research, belonging to the general problematic of fluid/structure interactions. Here, we are interested in modeling vesicles, capsules and RBCs using a boundary integral formulation, and focus on exact singularity subtractions of the kernel of the integral equations in 3D. In order to increase the precision of singular and near-singular integration, we propose here a refinement procedure in the vicinity of the pole of the Green-Oseen kernel. The refinement is performed homogeneously everywhere on the source surface in order to reuse the additional quadrature nodes when calculating boundary integrals in multiple target points. We also introduce a multi-level look-up algorithm in order to select the additional quadrature nodes in vicinity of the pole of the Green-Oseen kernel. The expected convergence rate of the proposed algorithm is of order 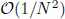while the computational complexity is of order 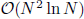, where N is the number of degrees of freedom used for surface discretization. Several numerical tests are presented to demonstrate the convergence and the efficiency of the method.

Keywords

64N3865N8074F1076Z05Stokes flowfluid structure interactionboundary integral methodred blood cellssingularity subtraction
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 7 , Issue 4 , November 2014 , pp. 413 - 434
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Seifert, U., Advances in Physics 46, 13 (1997).Google Scholar
[2] Barthès-Biesel, D., C.R. Physique 10, 764 (2009).Google Scholar
[3] Walter, J., Salsac, A.-V., Barthès-Biesel, D., and Le Tallec, P., International Journal for Numerical Methods in Engineering 83, 829 (2010).Google Scholar
[4] Biben, T., Farutin, A., and Misbah, C., Phys. Rev. E 83, 031921 (2011).CrossRefGoogle Scholar
[5] Boedec, G., Leonetti, M., and Jaeger, M., Journal of Computational Physics 230, 1020 (2011).CrossRefGoogle Scholar
[6] Zhao, H., Isfahani, A. H., Olson, L. N., and Freund, J. B., Journal of Computational Physics 229, 3726 (2010).Google Scholar
[7] Veerapaneni, S. K., Rahimian, A., Biros, G., and Zorin, D., Journal of Computational Physics 230, 5610 (2011).Google Scholar
[8] Zhao, H. and Shaqfeh, E. S. G., Journal of Fluid Mechanics 674, 578 (2011).Google Scholar
[9] Zhao, H., Spann, A. P., and Shaqfeh, E. S. G., Physics of Fluids 23, 121901 (pages 12) (2011).CrossRefGoogle Scholar
[10] Spann, A. P., Zhao, H., and Shaqfeh, E. S. G., Physics of Fluids (1994-present) 26, 031902 (2014).Google Scholar
[11] Noguchi, H. and Gompper, G., Proceedings of the National Academy of Sciences of the United States of America 102, 14159 (2005).Google Scholar
[12] Pivkin, I. V. and Karniadakis, G. E., Phys. Rev. Lett. 101, 118105 (2008).CrossRefGoogle Scholar
[13] Fedosov, D. A., Caswell, B., and Karniadakis, G. E., Biophysical Journal 98, 2215 (2010).Google Scholar
[14] Kraus, M., Wintz, W., Seifert, U., and Lipowsky, R., Phys. Rev. Lett. 77, 3685 (1996).CrossRefGoogle Scholar
[15] Cantat, I. and Misbah, C., Phys. Rev. Lett. 83, 235 (1999a).Google Scholar
[16] Pozrikidis, C., Journal of Computational Physics 169, 250 (2001).Google Scholar
[17] Dodson, W. R. and Dimitrakopoulos, P., Phys. Rev. Lett. 101, 208102 (2008).Google Scholar
[18] Bagchi, P. and Kalluri, R. M., Physical Review E 80, 016307 (2009).Google Scholar
[19] Clausen, J. and Aidun, C., Phys. Fluid 23, 123302 (2010).Google Scholar
[20] Dodson, W. R. and Dimitrakopoulos, P., Phys. Rev. E 85, 021922 (2012).CrossRefGoogle Scholar
[21] Kim, Y. and Lai, M.-C., Journal of Computational Physics 229, 4840 (2010).Google Scholar
[22] Vlahovska, P., Podgorski, T., and Misbah, C., Physique, C. R. 10, 775 (2009).Google Scholar
[23] Vlahovska, P., Barthès-Biesel, D., and Misbah, C., C.R. Physique 14, 451 (2013).Google Scholar
[24] Cantat, I. and Misbah, C., Phys. Rev. Lett. 83, 880 (1999b).Google Scholar
[25] Lac, E., Morel, A., and D. Barthès-Biesel, J. Fluid Mech. 573, 149 (2007).Google Scholar
[26] Veerapaneni, S. K., Gueyffier, D., Zorin, D., and Biros, G., J. Comp. Phys. 228, 2334 (2009).Google Scholar
[27] Batchelor, G. K., Journal of Fluid Mechanics 41, 545 (1970).Google Scholar
[28] Pozrikidis, C., Boundary Integral and Singularity Methods for Linearized Viscous Flow (Cambridge University Press, 1992).CrossRefGoogle Scholar
[29] Duffy, M. G., SIAM Journal on Numerical Analysis 19, 1260 (1982).Google Scholar
[30] Khayat, M. and Wilton, D., Antennas and Propagation, IEEE Transactions on 53, 3180 (2005).Google Scholar
[31] Klöckner, A., Barnett, A., Greengard, L., and M. O’Neil, Journal of Computational Physics 252, 332 (2013).CrossRefGoogle Scholar
[32] Klaseboer, E., Sun, Q., and Chan, D. Y. C., Journal of Fluid Mechanics 696, 468 (2012).Google Scholar
[33] Heltai, L., Arroyo, M., and DeSimone, A., Computer Methods in Applied Mechanics and Engineering 268, 514 (2014).Google Scholar
[34] Loewenberg, M. and Hinch, E. J., Journal of Fluid Mechanics 321, 395 (1996).Google Scholar
[35] Farutin, A., Biben, T., and Misbah, C., http://hal.archives-ouvertes.fr/hal-00841996 0, 000000 (2012).Google Scholar
[36] Slowicka, A. M., Ekiel-Jezewska, M. L., Sadlej, K., and Wajnryb, E., J. Chem. Phys. 136, 044904 (2012).CrossRefGoogle Scholar
[37] Slowicka, A. M., Wajnryb, E., and Ekiel-Jezewska, M. L., Eur. Phys. J. E 36, 31 (2013).CrossRefGoogle Scholar
[38] Maitre, E., Misbah, C., Peyla, P., and Raoult, A., Physica D 243, 1146 (2012).Google Scholar
[39] Laadhari, A., Saramito, P., and Misbah, C., Phys. Fluid 24, 031901 (2012).Google Scholar
[40] Doyeux, V., Guyot, Y., Chabannes, V., Prud’Homme, C., and Ismail, M., Journal of Computational and Applied Mathematics 246, 251 (2013).Google Scholar
[41] Salac, D. and Miksis, M., J. Comp. Phys. 230, 8192 (2011).Google Scholar
[42] Biben, T. and Misbah, C., Phys. Rev. E 67, 031908 (2003).Google Scholar
[43] Du, Q., Liu, C., and Wang, X., J. Comp. Phys. 198, 450 (2004).Google Scholar
[44] Du, Q., Liu, C., and Wang, X., J. Comp. Phys. 212, 757 (2006).Google Scholar
[45] Biben, T., Kassner, K., and Misbah, C., Phys. Rev. E 72, 041921 (2005).Google Scholar
[46] Kim, Y. and Lai, M.-C., Phys. Rev. E 86, 066321 (2012).Google Scholar