Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T11:46:58.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of a Streamline-Diffusion Finite Element Method on Bakhvalov-Shishkin Mesh for Singularly Perturbed Problem

Part of: Partial differential equations, boundary value problems

Published online by Cambridge University Press:  20 February 2017

Yunhui Yin ,
Peng Zhu  and
Bin Wang
Yunhui Yin*
Affiliation:
College of Mathematics Physics and Information Engineering, Jiaxing University, Jiaxing, Zhejiang 314001, China
Peng Zhu*
Affiliation:
College of Mathematics Physics and Information Engineering, Jiaxing University, Jiaxing, Zhejiang 314001, China
Bin Wang*
Affiliation:
College of Mechanical and Electrical Engineering, Jiaxing University, Jiaxing, Zhejiang 314001, China
*
*Corresponding author. Email addresses:[email protected] (Y. Yin), [email protected] (P. Zhu), [email protected] (B. Wang).
*Corresponding author. Email addresses:[email protected] (Y. Yin), [email protected] (P. Zhu), [email protected] (B. Wang).
*Corresponding author. Email addresses:[email protected] (Y. Yin), [email protected] (P. Zhu), [email protected] (B. Wang).
Get access

Abstract

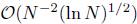In this paper, a bilinear Streamline-Diffusion finite element method on Bakhvalov-Shishkin mesh for singularly perturbed convection – diffusion problem is analyzed. The method is shown to be convergent uniformly in the perturbation parameter ∈ provided only that ∈ ≤ N–1. An convergent rate in a discrete streamline-diffusion norm is established under certain regularity assumptions. Finally, through numerical experiments, we verified the theoretical results.

Keywords

singularly perturbed problemStreamline-Diffusion finite element methodBakhvalov-Shishkin mesherror estimate

MSC classification

Secondary: 65N15: Error bounds 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 10 , Issue 1 , February 2017 , pp. 44 - 64
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Miller, J., O’Riordan, E., and Shishkin, G., Fitted Numerical Methods for Singular Perturbation Problems, World Scientific, Singapore, 2000.Google Scholar
[2] Roos, H.G., Layer adapted grids for singular perturbation problems, Z. Angew. Math. Mech., vol. 78 (1998), pp. 291–309.3.0.CO;2-R>CrossRefGoogle Scholar
[3] Roos, H.G., Stynes, M., and Tobiska, L., Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion-Reaction and Flow Problems, Springer, Berlin, 2008.Google Scholar
[4] Linss, T. and Stynes, M., Asymptotic analysis and Shishkin-type decomposition for an ellipyic convection-diffusion problem, J. Math. Anal. Appl., vol. 261 (2001), pp. 604–632.CrossRefGoogle Scholar
[5] Zhang, Z.M., Finite element superconvergent on shishkin mesh for 2-D convection-Diffusion problems, Mathematics of computation, vol. 72 (2003), pp. 1147–1177.CrossRefGoogle Scholar
[6] Apel, T. and Dobroeolski, M., Anisotropic interpolation with application to the finite element method, Computing, vol. 47 (1992), pp. 277–293.CrossRefGoogle Scholar
[7] Lin, Q. and Yan, N., The Construction Analysis of High Efficiency Finite Element, Hebei University Press, China, 1996 (in chinese).Google Scholar
[8] Linss, T., An upwind difference scheme on a novel Shishkin-type mesh for a linear convection-diffusion problem, J. Comput. Appl. Math., vol. 110 (1999), pp. 93–104.CrossRefGoogle Scholar
[9] Linss, T., Analysis of a Galerkin finite element on a Bakhvalov-Shishkin for a linear conmection-diffusion problem, IMA J. Numer. Anal., vol. 20 (2000), pp. 621–632.CrossRefGoogle Scholar
[10] Stynes, M. and Tobiska, L., The SDFEM for a convection-diffusion problem with a boundary layer: optimal error analysis and enhancement of accuracy, SIAM. J. Numer. Anal., vol. 41 (2003), pp. 1620–1642.CrossRefGoogle Scholar
[11] Johnson, C. and Saranen, J., Streamline diffusion methods for the incompressible Euler and Navier-Stocks equations, Math. Comp., vol. 47 (1986), pp. 1–18.CrossRefGoogle Scholar
[12] Linss, T. and Stynes, M., The SDFEM on Shishkin meshes for linear convection-diffusion problems, Numer. Math., vol. 87 (2001), pp. 457–484.CrossRefGoogle Scholar
[13] Stynes, M. and Tobiska, L., Analysis of the streamline-diffusion finite element method on a Shishkin mesh for a convection-diffusion problem with exponential layers, J. Numer. Math., vol. 9 (2001), pp. 59–76.CrossRefGoogle Scholar
[14] Ciarlet, P. G., The Finite Element Method for Elliptic Problems, North-Holland, Amsterdam, 1978.Google Scholar
[15] Linss, T. and Stynes, M., Numerical methods on Shishkin meshes for linear convection-diffusion problems, Comput. Methods Appl. Mech. Eng., vol. 190 (2001), pp. 3527–3542.CrossRefGoogle Scholar
[16] Hughes, T.J.R. and Brooks, A., A multidimensional upwise scheme with no crossind difflusion, in Finite element methods for convection dominated flows, ASME, AMD-34 (1979), pp. 19-35.Google Scholar