Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T18:16:46.539Z Has data issue: false hasContentIssue false
  • English
  • Français

The Gradient Superconvergence of Bilinear Finite Volume Element for Elliptic Problems

Part of: Partial differential equations, boundary value problems Partial differential equations, initial value and time-dependent initial-boundary value problems

Published online by Cambridge University Press:  17 November 2016

Tie Zhang  and
Lixin Tang
Tie Zhang*
Affiliation:
Department of Mathematics and the State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang 110004, China
Lixin Tang*
Affiliation:
Department of Mathematics and the State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang 110004, China
*
*Corresponding author. Email addresses:[email protected] (T. Zhang), [email protected] (L.-X. Tang)
*Corresponding author. Email addresses:[email protected] (T. Zhang), [email protected] (L.-X. Tang)
Get access

Abstract

We study the gradient superconvergence of bilinear finite volume element (FVE) solving the elliptic problems. First, a superclose weak estimate is established for the bilinear form of the FVE method. Then, we prove that the gradient approximation of the FVE solution has the superconvergence property:

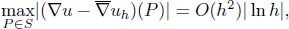
where 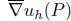denotes the average gradient on elements containing point P and S is the set of optimal stress points composed of the mesh points, the midpoints of edges and the centers of elements.

Keywords

Bilinear finite volume elementelliptic problemgradient approximationsuperconvergence

MSC classification

Secondary: 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods 65M60: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 9 , Issue 4 , November 2016 , pp. 579 - 594
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Cai, Z.Q., On the finite volume element method, Numer. Math., 58 (1991), pp. 713–735.Google Scholar
[2] Chen, Z.Y., L2 estimate of linear element generalized difference schemes, Acta. Sci. Nat. Univ. Sunyatseni, 33 (1994), pp. 22–28.Google Scholar
[3] Chen, Z.Y., Superconvergence of generalized difference methods for elliptic boundary value problem, Numer. Math. A J. of Chinese Univ.(English Ser), 3 (1994), pp. 163–171.Google Scholar
[4] Chen, Z.Y., Li, R.H. and Zhou, A.H., A note on the optimal L2-estimate of the finite volume element method, Adv. Comput. Math., 16 (2002), pp. 291–303.Google Scholar
[5] Chen, L., A new class of high order finite volume element methods for second order elliptic equations, SIAM J. Numer. Anal., 47 (2010), pp. 4021–4023.Google Scholar
[6] Chou, S.H. and Li, Q., Error estimates in L2, H1, L∞ in covolume methods for elliptic and parabolic problem: a unified approach, Math. Comp., 69 (2000), pp. 103–120.Google Scholar
[7] Chou, S.H. and Ye, X., Superconvergence of finite volume methods for the second order elliptic problem, Comput. Methods Appl. Mech. Engrg., 196 (2007), pp. 3706–3712.Google Scholar
[8] Ewing, R.E., Lin, T. and Lin, Y.P., On the accuracy of the finite volume element method based on piecewise linear polynomials SIAM J. Numer. Anal., 39 (2002), pp. 1865–1888.CrossRefGoogle Scholar
[9] Lazarov, R., Michev, I. and Vassilevski, P., Finite volumemethods for convection-diffusion problems, SIAM J. Numer. Anal., 33 (1996), pp. 31–55.Google Scholar
[10] Li, R.H., Chen, Z.Y. and Wu, W., Generalized difference methods for differential equations: numerical analysis of finite volume methods, Marcel, New York, 2000.Google Scholar
[11] Lin, Q. and Zhu, Q.D., The preprocessing and postprocessing for the finite element methods, Shanghai Sci & Tech Publishing, Shanghai, 1994.Google Scholar
[12] Lv, J.L. and Li, Y.H., L2 error estimates and superconvergence of the finite volume element methods on quadrilateral meshes, Adv. Comput. Math., 37 (2012), pp. 393–416.CrossRefGoogle Scholar
[13] Süli, E., Convergence of finite volume schemes for poission's equation on nonuniform meshes, SIAM J. Numer. Anal., 28 (1991), pp. 1419–1430.Google Scholar
[14] Wu, H.J. and Li, R.H., Error estimate for finite volume element methods for general second order elliptic problem, Numer. Meth. PDEs., 19 (2003), pp. 693–708.Google Scholar
[15] Xu, J.C. and Zou, Q.S., Analysis of linear and quadratic simplical finite volume methods for elliptic equations, Numer. Math., 111 (2009), pp. 469–492.Google Scholar
[16] Zhang, L. and Li, L.K., On superconvergence of isopareametric bilinear finite elements, Comm. Numer. Meth. Enrg., 12 (1996), pp. 849–862.3.0.CO;2-N>CrossRefGoogle Scholar
[17] Zhang, T., Lin, Y.P. and Tait, R.J., On the finite volume element version of Ritz-Volterra projection and applications to related equations, J. Comp. Math., 20 (2002), pp. 491–504.Google Scholar
[18] Zhang, T. and Sheng, Y., Superconvergence and Gradient Recovery for a Finite Volume Element Method for Solving Convection-Diffusion Equations, Numer. Meth. PDEs., 30 (2014), pp. 1152–1168.Google Scholar
[19] Zhang, T., Finite element methods for partial differential-integral equations, Science Press, Beijing, 2009.Google Scholar
[20] Zhang, Z.M. and Zou, Q.S., Some recent advances on vertex centered finite volume element methods for elliptic equations, Sci. China Mathematics, 56 (2013), pp. 2507–2522.Google Scholar
[21] Zhu, Q.D. and Lin, Q., The superconvergence theory of finite elements, Hunan Science and Technology Publishing House, Changsha, 1989.Google Scholar