No CrossRef data available.
Article contents
The Bases of the Non-Uniform Cubic Spline Space
Published online by Cambridge University Press: 28 May 2015
Abstract
In this paper, the dimension of the nonuniform bivariate spline space 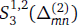 is discussed based on the theory of multivariate spline space. Moreover, by means of the Conformality of Smoothing Cofactor Method, the basis of
is discussed based on the theory of multivariate spline space. Moreover, by means of the Conformality of Smoothing Cofactor Method, the basis of 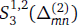 composed of two sets of splines are worked out in the form of the values at ten domain points in each triangular cell, both of which possess distinct local supports. Furthermore, the explicit coefficients in terms of B-net are obtained for the two sets of splines respectively.
composed of two sets of splines are worked out in the form of the values at ten domain points in each triangular cell, both of which possess distinct local supports. Furthermore, the explicit coefficients in terms of B-net are obtained for the two sets of splines respectively.
Keywords
- Type
- Research Article
- Information
- Numerical Mathematics: Theory, Methods and Applications , Volume 5 , Issue 4 , November 2012 , pp. 635 - 652
- Copyright
- Copyright © Global Science Press Limited 2012


