2.1. Task formulation

End-to-end coreference resolution is the state-of-the-art approach based on deep learning. It tackles mention detection and coreference resolution simultaneously by span ranking; thus, it is formulated as a task of assigning antecedents $a_i$ for each span $i$ . A possible span candidate is any continuous N-gram within a sentence. The set of possible assignments $a_i$ is $\mathcal{A}_i=\{1,\dots, i-1,\varepsilon \}$ , where $\varepsilon$ is a “dummy” antecedent. If span $i$ is assigned to a non-dummy antecedent, span $j$ , then we have $a_i = j$ . If span $i$ is assigned to a dummy antecedent $\varepsilon$ , then it indicates one of two scenarios: (1) span $i$ is not an entity mention; (2) span $i$ is the first mention of a new entity (cluster). Through transitivity of coreferent antecedents, these assignment decisions induce clusters of entities over the document.

2.2. First-order coreference resolution

The first-order end-to-end coreference resolution model (Lee et al. Reference Lee, He, Lewis and Zettlemoyer2017b) independently ranks each pair of spans using a pairwise scoring function $s(i,j)$ . These scores are used to compute the antecedent distribution $P(a_i)$ for each span $i$ :

(1) \begin{equation} P(a_i) = \frac{e^{s(i, a_i)}}{\sum _{j \in \mathcal{A}_i} e^{s(i,j)}} \end{equation}

The coreferent score $s(i,j)$ for a pair of spans includes three factors: (1) $s_m(i)$ , the score of span $i$ for being a mention, (2) $s_m(j)$ , the score of span $j$ for being a mention, (3) $s_a(i,j)$ , the score of span $j$ for being an antecedent of $i$ :

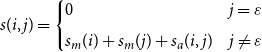(2) \begin{equation} \begin{aligned} s(i,j)= \begin{cases} 0& j=\varepsilon \\[5pt] s_m(i)+s_m(j)+s_a(i,j) & j \neq \varepsilon \\ \end{cases} \end{aligned} \end{equation}

The scoring functions $s_m$ and $s_a$ take span representations $\textbf{g}$ as input:

(3) \begin{equation} \begin{aligned} s_m(i)&=\textbf{w}_m \cdot FFNN_m(\textbf{g}_i) \\[3pt] s_a(i,j)&=\textbf{w}_a \cdot FFNN_a\left(\left[\textbf{g}_i,\textbf{g}_j,\textbf{g}_i \circ \textbf{g}_j,\phi (i,j)\right]\right) \end{aligned} \end{equation}

where $ \cdot$ denotes the dot product; $ \circ$ denotes element-wise multiplication; $FFNN$ denotes a feed-forward neural network; and $\phi (i,j)$ represents speaker and meta-data features (e.g., genre information and the distance between the two spans).

However, it is intractable to score every pair of spans in a document. There are $O(W^2)$ spans of potential mentions in a document ( $W$ is the number of words). Comparing every pair would be $O(W^4)$ complexity. Thus, pruning is performed according to the mention scores $s_m(i)$ to reduce the spans that are unlikely to be an entity mention.

2.3. Higher-order coreference resolution

The first-order coreference resolution model only considers pairs of spans, and does not directly incorporate any information about the entities to which the spans might belong. Thus, first-order models may suffer from consistency errors. HOI methods were proposed to incorporate some document-level information. Span-refinement-based HOI methods, such as AA (Lee et al., Reference Lee, He and Zettlemoyer2018; Joshi et al. Reference Joshi, Levy, Zettlemoyer and Weld2019, Reference Kantor and Globerson2020), Entity Equalization (Kantor and Globerson, Reference Kantor and Globerson2019), and Span Clustering (Xu and Choi, Reference Xu and Choi2020), iteratively refine span embeddings $\textbf{g}_i$ using global context. Cluster Merging (Xu and Choi, Reference Xu and Choi2020) is a score-based HOI method. It does not update span embeddings directly, but updates the coreferent scores using a latent cluster score.

AA (Lee et al., Reference Lee, He and Zettlemoyer2018) was the first HOI method. It iteratively refines the span representations $\textbf{g}^n_i$ of span $i$ at the $n$ th iteration, using information from antecedents. The refined span representations are used to compute the refined antecedent distribution $P_n(a_i)$ :

(4) \begin{equation} P_n(a_i) = \frac{e^{s\left(\textbf{g}_i^n, \textbf{g}^n_{a_i}\right)}}{\sum _{j\in \mathcal{A}_i} e^{s\left(\textbf{g}_i^n, \textbf{g}^n_j\right)}} \end{equation}

At each iteration, the expected antecedent representation $\textbf{a}^n_i$ of each span $i$ is computed using the current antecedent distribution $P_n(a_i)$ as an attention mechanism:

(5) \begin{equation} \textbf{a}_i^n = \sum \limits _{j \in \mathcal{A}_i} P_n(j) \textbf{g}_j^n \end{equation}

The current span representation $\textbf{g}_i^n$ is then updated via interpolation with its expected antecedent representation $\textbf{a}_i^n$ :

(6) \begin{equation} \textbf{g}_i^{n+1} = \textbf{f}_i^n \circ \textbf{g}_i^n + \left(1-\textbf{f}_i^n\right) \circ \textbf{a}_i^n \end{equation}

where $\textbf{f}_i^n = \sigma \left(\textbf{W}_f\left[ \textbf{g}_i^n, \textbf{a}_i^n\right]\right)$ is a learned gate vector, and $\circ$ denotes element-wise multiplication. Thus, the span representation $\textbf{g}_i^{n+1}$ at iteration $n+1$ is an element-wise weighted average of the current span representation $\textbf{g}_i^n$ and its direct antecedents.

2.4. Building span embeddings from contextualized representations

The core of end-to-end neural coreference resolution is the learning of vectorized representations of text spans. The span representation $\textbf{g}_i$ of span $i$ is usually the concatenation of four vectors (Lee et al. Reference Lee, He, Lewis and Zettlemoyer2017b) as follows:

(7) \begin{equation} \textbf{g}_i=\left[\textbf{g}^*_{START(i)},\textbf{g}^*_{END(i)},\hat{\textbf{g}}_i,\phi (i)\right] \end{equation}

where $START(i)$ and $END(i)$ are the start position and end position of span $i$ , respectively, Boundary representations $\textbf{g}^*_{START(i)},\textbf{g}^*_{END(i)}$ are the vector representations of word $START(i)$ and $END(i)$ , respectively. Internal representation $\hat{\textbf{g}}_i$ is a weighted sum of word vectors in span $i$ , and $\phi (i)$ is a feature vector encoding the size of span $i$ .

Assuming the vector representations of each word are $\{\textbf{x}_1,\cdots, \textbf{x}_T\}$ ( $T$ is the length of the document), Lee et al. (Reference Lee, He, Lewis and Zettlemoyer2017b), Zhang et al. (Reference Zhang, Nogueira dos Santos, Yasunaga, Xiang and Radev2018) and Lee et al. (Reference Lee, He and Zettlemoyer2018) use a bi-directional LSTM to build the first three vectors of the span representation $\textbf{g}_i$ :

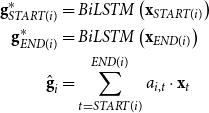(8) \begin{equation} \begin{aligned} \textbf{g}^*_{START(i)} &= BiLSTM\left(\textbf{x}_{START(i)}\right) \\ \textbf{g}^*_{END(i)} &= BiLSTM\left(\textbf{x}_{END(i)}\right)\\ \hat{\textbf{g}}_i&=\sum \limits ^{END(i)}_{t=START(i)} a_{i,t} \cdot \textbf{x}_t \end{aligned} \end{equation}

where $a_{i,t}$ is a learned weight computed from $BiLSTM(\textbf{x}_t)$ , and $\textbf{x}_t$ can be GloVe (Jeffrey Pennington, Socher, and Manning, Reference Pennington, Socher and Manning2014; Lee et al. Reference Lee, He, Lewis and Zettlemoyer2017b), ELMo (Lee et al., Reference Lee, He and Zettlemoyer2018; Peters et al., Reference Peters, Neumann, Iyyer, Gardner, Clark, Lee and Zettlemoyer2018), or the concatenation of GloVe and CNN character embeddings (Santos and Zadrozny, Reference Santos and Zadrozny2014; Zhang et al., Reference Zhang, Nogueira dos Santos, Yasunaga, Xiang and Radev2018).

Following the success of contextualized representations, Kantor and Globerson (Reference Kantor and Globerson2019), and Joshi et al. (Reference Joshi, Levy, Zettlemoyer and Weld2019) replace the LSTM-based encoder with BERT (Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019). They either use BERT in a convolutional mode (Kantor and Globerson, Reference Kantor and Globerson2019) or split the documents into fixed length before applying BERT (Joshi et al., Reference Joshi, Levy, Zettlemoyer and Weld2019). Kantor and Globerson (Reference Kantor and Globerson2019) use a learnable weighted average of the last four layers of BERT to build span representations. Joshi et al. (Reference Joshi, Levy, Zettlemoyer and Weld2019) use the topmost layer output of BERT to build span representations:

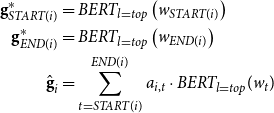(9) \begin{equation} \begin{aligned} \textbf{g}^*_{START(i)} &= BERT_{l=top}\left(w_{START(i)}\right) \\ \textbf{g}^*_{END(i)} &= BERT_{l=top}\left(w_{END(i)}\right)\\ \hat{\textbf{g}}_i&=\sum \limits ^{END(i)}_{t=START(i)} a_{i,t} \cdot BERT_{l=top}(w_t) \end{aligned} \end{equation}

where $BERT_l(w_i)$ is the $l$ th layer contextualized embeddings of token $w_i$ , and $a_{i,t}$ is a learned weight computed from the topmost layer output. Documents are split into segments of fixed length and BERT is applied to each segment. Two variants of splitting were proposed: overlap and independent (non-overlapping). Surprisingly, independent splitting performs better.

3.1. Effectiveness of higher-order inference

Lee et al. (Reference Lee, He and Zettlemoyer2018) propose the first HOI method, AA, for coreference resolution. Their experiments show that AA improved ELMo’s performance on OntoNotes by + 0.4 F1. Kantor and Globerson (Reference Kantor and Globerson2019) show that removing AA improved BERT’s performance slightly. Experiments by Xu and Choi (Reference Xu and Choi2020) show that span-refinement-based HOI methods, AA, Entity Equalization (Kantor and Globerson, Reference Kantor and Globerson2019), and Span Clustering (Xu and Choi, Reference Xu and Choi2020), have a negative impact on contextualized encoders, such as SpanBERT. However, the reasons behind this are not clear. In particular, the discrepancy of HOI impact among ELMo, BERT, and SpanBERT is not explained.

3.2. Measures of anisotropy and contextuality

Ethayarajh (Reference Ethayarajh2019) proposes to measure how contextual and anisotropic a word representation is using three different metrics: self-similarity, intra-sentence similarity, and random similarity. We adopt their measures to gauge how anisotropic and how contextual a word representation or a span embedding is and show that the HOI methods actually increase the anisotropy of span embeddings.

3.3. Data augmentation for coreference resolution

Wu et al. (Reference Wu, Wang, Yuan, Wu and Li2020) use existing question answering datasets for out-of-domain data augmentation for coreference resolution by transforming the coreference resolution task into a question answering task. To reduce anisotropy with examples of related but distinct entities, we use synthesized documents for in-domain data augmentation.

3.4. Embeddings aggregation

Arora et al. (Reference Arora, Li, Liang, Ma and Risteski2018) hypothesize that the global word embedding is a linear combination of its sense embeddings. They show that senses can be recovered through sparse coding. Mu et al. (Reference Mu, Bhat and Viswanath2017) show that senses and word embeddings are linearly related and sense sub-spaces tend to intersect along a line. Yaghoobzadeh et al. (Reference Yaghoobzadeh, Kann, Hazen, Agirre and Schütze2019) probe the aggregated word embeddings of polysemous words for semantic classes. They created a WIKI-PSE corpus, where word and semantic class pairs were annotated using Wikipedia anchor links, for example “apple” has two semantic classes: food and organization. A separate embedding for each semantic class was learned based on the WIKI-PSE corpus. They find that the linearly aggregated embeddings of polysemous words represent their semantic classes well. Our previous work (Hou et al. Reference Hou, Wang, He and Zhou2020) shows that linearly aggregated entity embeddings can improve the performance of entity linking. In this research, we use linear aggregations of contextualized representations from different layers of Transformer (Vaswani et al. Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser and Polosukhin2017)-based encoders to learn less-anisotropic span embeddings.

4.1. What is anisotropy

Anisotropy means that the elements of vectorized representations are not uniformly distributed with respect to direction. Instead, they occupy a narrow cone in the vector space. Its opposite, isotropy, has both theoretical and empirical benefits, for example it allows for stronger “self-normalization” during training (Arora, Liang, and Ma, Reference Arora, Liang and Ma2017) and improves performance on downstream tasks (Mu et al., Reference Mu, Bhat and Viswanath2018).

4.2. Measure of anisotropy of span embeddings

For contextualized word representations, the degree of anisotropy is measured by the average cosine similarity between the representations of randomly sampled words from different contexts (Ethayarajh, Reference Ethayarajh2019). We adopt this to measure the anisotropy, $RandomSim(D)$ , of span embeddings in a document $D$ , as follows.

Let $D$ be a document that contains $m$ spans of entity mentions $\{s_1, s_2, \dots, s_m\}$ . Let $\textbf{g}_i$ be the span embedding of span $s_i$ . The random similarity between these spans is

(10) \begin{equation} RandomSim(D) = \frac{1}{m^2-m}\sum \limits _{i} \sum \limits _{j\neq i}cos\left(\textbf{g}_i, \textbf{g}_j\right) \end{equation}

where $cos$ denotes the cosine similarity.

4.3. HOI generates more anisotropic span embeddings

In this subsection, we prove and show that HOI makes the generated span embeddings more anisotropic. According to Equation (10), we need to prove that the HOI refined span embeddings $\textbf{g}_i^{n+1}, \textbf{g}_j^{n+1}$ at iteration $n+1$ are more similar than $\textbf{g}_i^{n}, \textbf{g}_j^{n}$ at iteration $n$ . Based on the definition $cos(\textbf{a}, \textbf{b})=\textbf{a}\cdot \textbf{b}/\|\textbf{a}\|\times \|\textbf{b}\|$ and the supposition that $\|\textbf{g}_i^{n+1}\|=\|\textbf{g}_i^n\|$ , we can say that $\textbf{g}_i^{n+1}, \textbf{g}_j^{n+1}$ are more similar than $\textbf{g}_i^{n}, \textbf{g}_j^{n}$ if $\textbf{g}_i^{n+1}\cdot \textbf{g}_j^{n+1} \gt \textbf{g}_i^{n}\cdot \textbf{g}_j^{n}$ .

Combining Equations (5) and (6) and treat vector $\textbf{f}_i^n$ as scalar $f_i^n$ , we get

(11) \begin{equation} \begin{aligned} \textbf{g}_i^{n+1} &= f_i^n \textbf{g}_i^n + \left(1-f_i^n\right) \sum _{k=1}^{m} P_n(k) \textbf{g}_k^n \approx f_i^n \textbf{g}_i^n + \left(1-f_i^n\right) \Big (P_n(i) \textbf{g}_i^n + P_n(j) \textbf{g}_j^n\Big )\\[5pt] \textbf{g}_j^{n+1} &= f_j^n \textbf{g}_j^n + \left(1-f_j^n\right) \sum _{k=1}^{m} P^{\prime}_n(k) \textbf{g}_k^n \approx f_j^n \textbf{g}_j^n + \left(1-f_j^n\right) \Big (P^{\prime}_n(i) \textbf{g}_i^n + P^{\prime}_n(j) \textbf{g}_j^n\Big ) \end{aligned} \end{equation}

Treating $f_i^n$ and $f_j^n$ equally as $f$ , $P_n(i)$ and $P^{\prime}_n(j)$ equally as $P$ , $P_n(j)$ and $P^{\prime}_n(i)$ equally as $\hat{P}$ , we get

(12) \begin{equation} \textbf{g}_i^{n+1} \cdot \textbf{g}_j^{n+1} \approx \Big (f\textbf{g}_i^n + (1-f)\left(P\textbf{g}_i^n+\hat{P}\textbf{g}_j^n\right)\Big ) \cdot \Big (f\textbf{g}_j^n + (1-f)\left(\hat{P}\textbf{g}_i^n+P\textbf{g}_j^n\right)\Big ) \end{equation}

and

(13) \begin{align} \textbf{g}_i^{n+1} \cdot \textbf{g}_j^{n+1} \approx & \Big (f^2+2f(1-f)P+(1-f)^2P^2+(1-f)^2\hat{P}^2\Big ) \textbf{g}_i^n\cdot \textbf{g}_j^n\nonumber\\[4pt] &+2f(1-f)\hat{P}+2(1-f)^2P\hat{P} \end{align}

Figure 1 shows the histogram distribution of the $f$ and $P$ values. Practically, as shown in Figure 1, $f,P\rightarrow 1$ , and as $P,\hat{P}$ are the elements of a softmax list, $P+\hat{P}\approx 1$ , $\hat{P}\rightarrow 0$ . Thus, in Equation (13), the former part approximately equals $\textbf{g}_i^n\cdot \textbf{g}_j^n$ , and the latter part is not zero. Thus, $\textbf{g}_i^{n+1}\cdot \textbf{g}_j^{n+1} \gt \textbf{g}_i^{n}\cdot \textbf{g}_j^{n}$ . This proves that the HOI methods tend to generate more anisotropic span embeddings. From Equation (13), we can see that the more iterations we refine the span embeddings for, the more anisotropic the span embeddings will become.

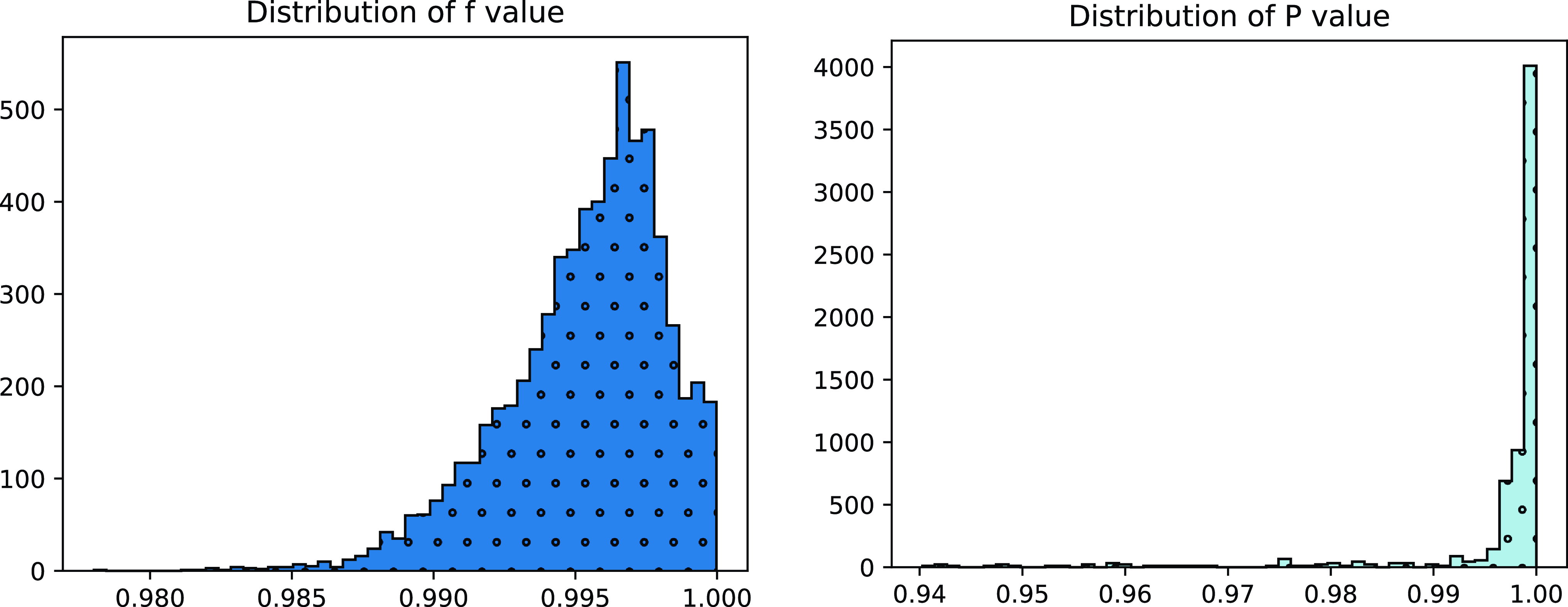
Figure 1. The histogram distributions of $f$ and $P$ values. We recorded 6564 $f$ and $P$ values respectively during the last two epochs of training C2F+BERT-base+AA. $f$ is the average across the embedding dimension; $P$ is the max value of antecedents.

To concretely show the degree of anisotropy of span embeddings generated by different HOI methods, we compute and record the random similarity (Equation (10)) at each epoch during training. Figure 2 displays the recorded average cosine similarity of each epoch. As shown in Figure 2, the span embeddings generated by HOI methods are always more anisotropic than the span embeddings generated without HOI.

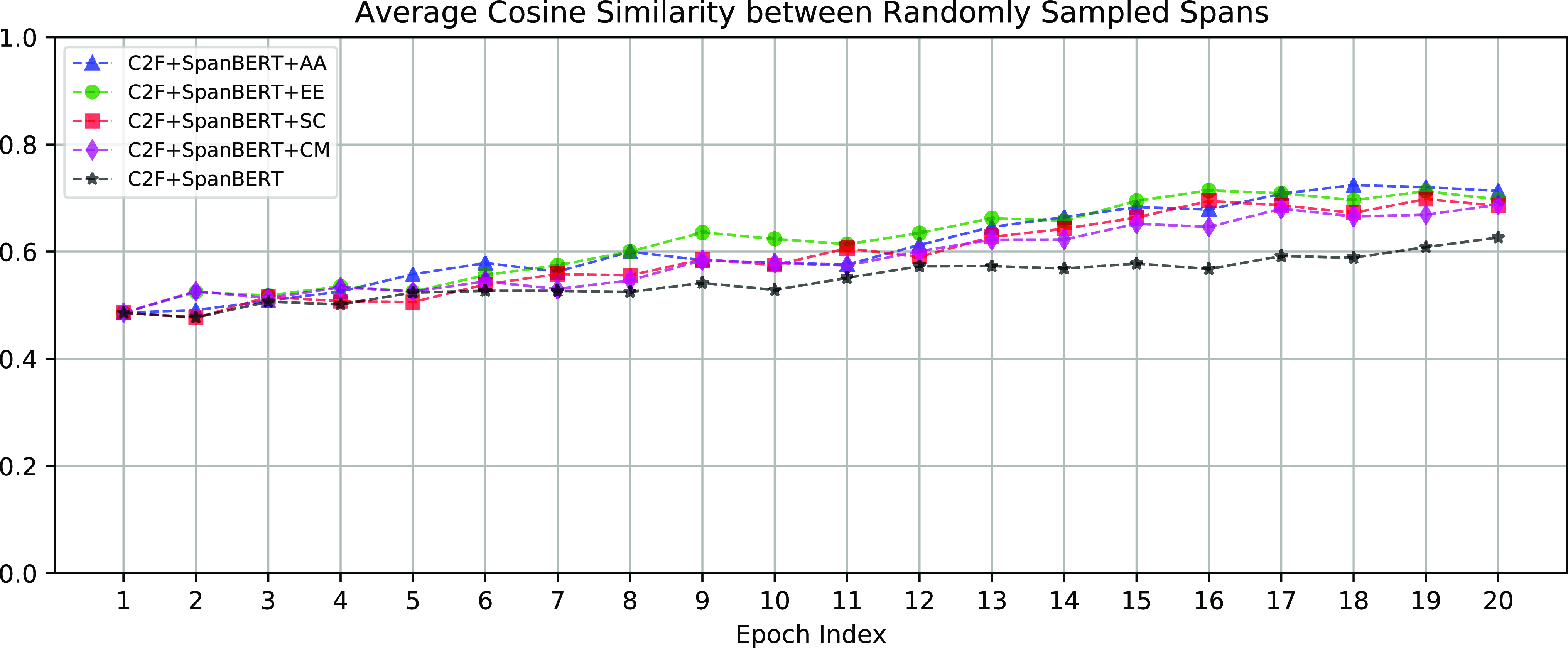
Figure 2. The degree of anisotropy of span embeddings is measured by the average cosine similarity between uniformly randomly sampled spans. (Figures 2-6 are generated using the method of Ethayarajh (Reference Ethayarajh2019)).

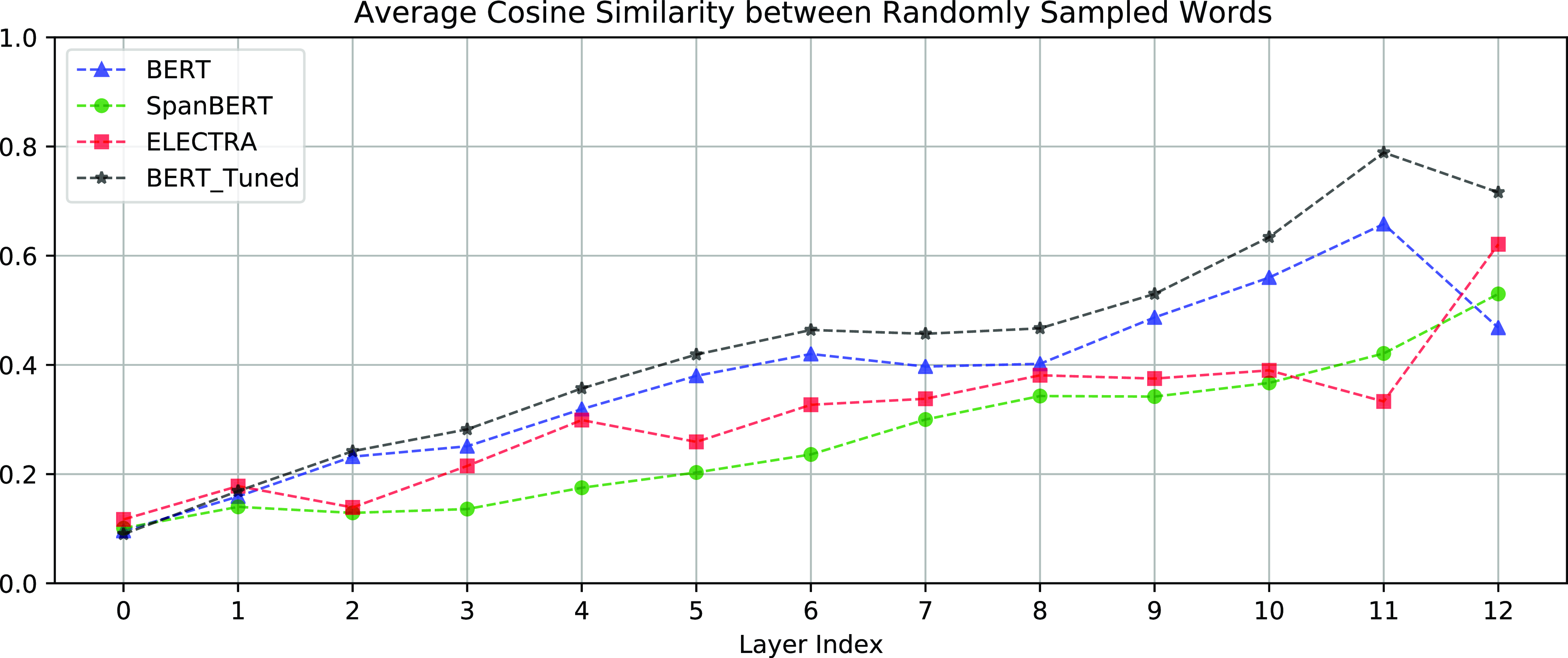
Figure 3. For contextualized word representations, the degree of anisotropy is measured by the average cosine similarity between uniformly randomly sampled words. The higher the layer, the more anisotropic. Embeddings of layer 0 are the input layer word embeddings.

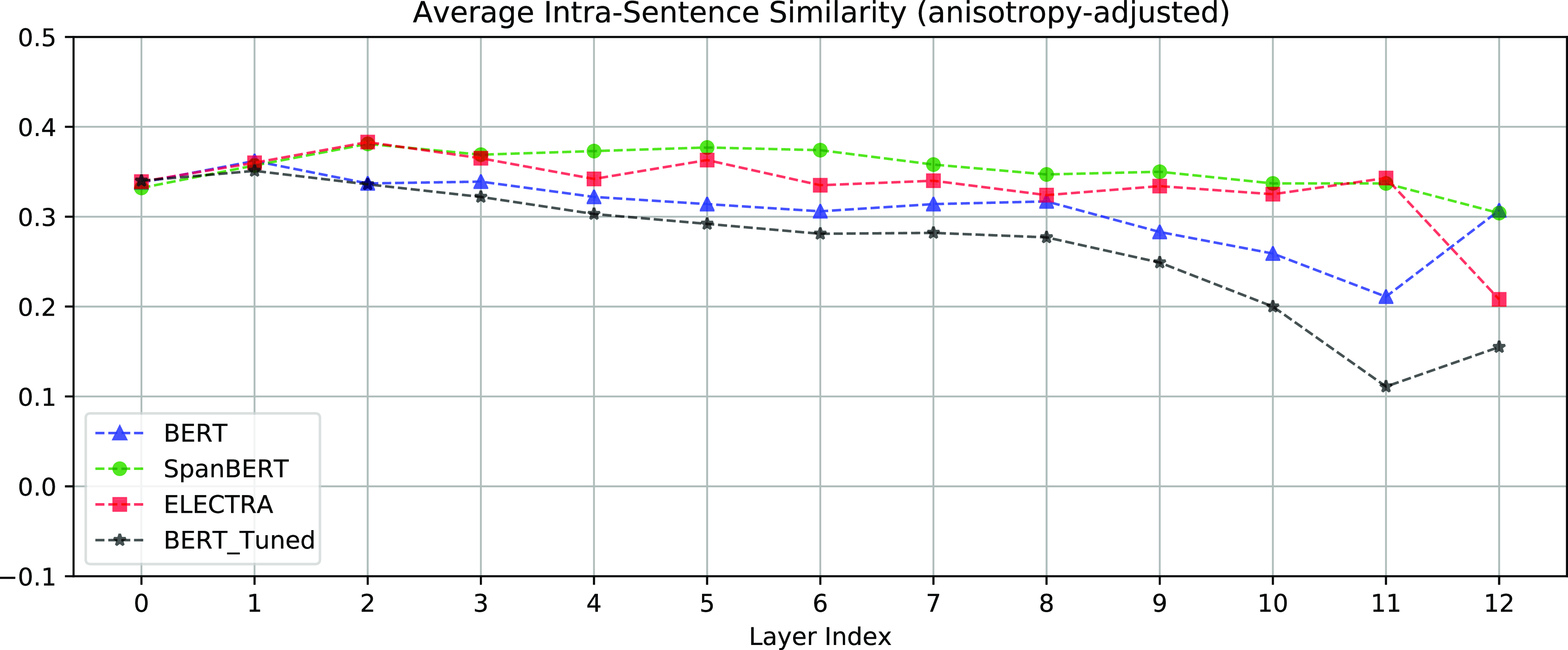
Figure 4. Intra-sentence similarities of contextualized representations. The intra-sentence similarity is the average cosine similarity between each word representation in a sentence and their mean.

Figure 5. Self-similarities of contextualized representations. Self-similarity is the average cosine similarity between representations of the same word in different contexts.

According to Equations (5) and (6), higher-order span refinement is essentially injecting information from other spans into a span’s embedding. Thus, unrelated spans may become more similar (and hence, more anisotropic).

4.4. Why anisotropic span embeddings are undesirable

Span embeddings encode the contextual information (and some meta-information about spans) of the textual spans that are potentially an entity mention. Spans in the same sentence or segment will have similar span embeddings. Thus, some degree of anisotropy is also an indicator of contextuality (Ethayarajh, Reference Ethayarajh2019). To explain this, we compute the measures of contextualization and anisotropy proposed by Ethayarajh (Reference Ethayarajh2019) and visualize these measures in Figures 3, 4, and 5. Figure 3 shows the random cosine similarities (the degree of anisotropy) of each layer. Figures 4 and 5 show the intra-sentence similarities and self-similarities of each layer, respectively. Both the intra-sentence similarity and the self-similarity are contextualization measures proposed by Ethayarajh (Reference Ethayarajh2019). As shown in Figures 4 and 5, the higher layer representations are more context-specific, that is the top layer representations are more contextualized. As shown in Figure 3, the top layer representations are also more anisotropic. However, if the embeddings of the spans in the same document are too anisotropic, that is the span embeddings occupy a narrow cone in the vector space, related but distinct entities (e.g., pilots and flight attendants) will become difficult to distinguish.

This can be explained by the example of pilots and flight attendants by Lee et al. (Reference Lee, He, Lewis and Zettlemoyer2017b). As Lee et al. (Reference Lee, He, Lewis and Zettlemoyer2017b) analyzed, related but distinct entities appear in similar contexts and likely have nearby word (span) embeddings. Thus, their neural coreference resolution model predicts a false positive link between pilots and flight attendants. Related entities are grouped in a local cluster in the vector space, while unrelated entities in different contexts are grouped in different clusters in the vector space. Thus, unrelated entities are more distinguishable than the related entities. However, extremely isotropic (not anisotropic) embeddings are also undesirable. For a vocabulary with $V$ words, the extremely isotropic embeddings would be the embeddings in a $|V|$ dimension with each word occupying a single dimension. Such extremely isotropic embeddings cannot capture the similarity between words and lose contextualization. As more contextualized representations tend to be anisotropic (Ethayarajh, Reference Ethayarajh2019), we need to achieve a trade-off between isotropy and contextualization.

In summary, we believe that the negative impact of HOI is caused by worsening the anisotropy of span embeddings without incorporating more contexts. We propose methods that learn less-anisotropic span embeddings in Section 5 and perform comprehensive experimental analysis in Section 6.

5.1. Less-anisotropic internal representations (LAIR)

Contextualized word representations are more context-specific in the higher layers. However, Ethayarajh (Reference Ethayarajh2019) shows that these contextualized word representations are anisotropic, especially in the higher layers. Building span embeddings directly from the output-layer contextualized word representations will cause anisotropy. To reduce the degree of anisotropy while retaining contextual information, we use a linear aggregation of the contextualized embeddings of the first layer and the topmost layer. As the boundary representations need to encode more contextual information, we only use aggregated embeddings for the internal representation $\hat{\textbf{g}}_i$ :

(14) \begin{equation} \begin{aligned} AT(w_t) &= \alpha \circ T_{l=1}(w_t) + (1-\alpha ) \circ T_{l=top}(w_t)\\ \textrm{a}_{t} &= \textbf{w}_{\textrm{a}} \cdot FFNN_{\textrm{a}}(AT(w_t))\\ a_{i,t} &= \frac{exp(\textrm{a}_t)}{\sum \limits ^{END(i)}_{k=START(i)}exp(\textrm{a}_k)}\\ \hat{\textbf{g}}_i&=\sum \limits ^{END(i)}_{t=START(i)} a_{i,t} \cdot AT(w_t) \end{aligned} \end{equation}

where $T_l(w)$ is the $l$ th layer Transformer-based (Vaswani et al., Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser and Polosukhin2017) contextualized embedding of token $w$ , $AT$ is the aggregated representation, and the scalar $\alpha$ is the weight of the first layer embedding.

Aggregating the first layer and the topmost layer embeddings can reduce anisotropy without substantial loss of contextual information, because the topmost layer encodes the most contextual information, and the first layer is the least anisotropic (Ethayarajh, Reference Ethayarajh2019).

5.2. Data augmentation with document synthesis and mention swap (DSMS)

As we mentioned in Section 4.4, anisotropic span embeddings make it difficult to distinguish related but distinct entities. We propose to learn less-anisotropic span embeddings by using a more diversified set of examples of related but distinct entities, generated by synthesizing documents and by mention swapping. Algorithm 1 describes the complete process for this data augmentation method, the details of which are as follows.

Algorithm 1: Data augmentation for learning less-anisotropic span embeddings

6.1. Data sets and evaluation metrics

6.2. Implementation and hyperparameters

Before performing the experiments on coreference resolution, we gauged the anisotropy and contextuality of the contextualized representations from BERT, SpanBERT, and ELECTRA using the codeFootnote b from Ethayarajh (Reference Ethayarajh2019) on the data sets mentioned in Section 6.1.3. The results for anisotropy are shown in Figure 3. The measures of contextuality are intra-sentence similarity and self-similarity, shown in Figures 4 and 5 respectively.

We split the OntoNotes English documents into segments of 512 word pieces (Wu et al., Reference Wu, Schuster, Chen, Le, Norouzi, Macherey, Krikun, Cao, Gao and Macherey2016), performing data augmentation only on the training set. To compare the effects of our methods on multiple encoders, we also carried out experiments on ELECTRA with uncased vocabulary, using the HuggingFace PyTorch version of ELECTRAFootnote c (discriminator).

Our code is based on the implementation in Joshi et al. (Reference Joshi, Levy, Zettlemoyer and Weld2019) and Xu and Choi (Reference Xu and Choi2020). We use similar hyperparameters, except that we introduce a new hyperparameter: the weight of the first layer embeddings, $\alpha$ , in Equation (14). We chose $\alpha$ as follows: For SpanBERT, we tried $\alpha$ over the range from 0.1 to 0.6 with a 0.1 increment. Since ELECTRA is more anisotropic than SpanBERT (as shown in Figure 3), we tried larger values of $\alpha$ for ELECTRA. All the $\alpha$ values are chosen based on the development set of OntoNotes. These hyperparameters for our experiments are listed in Table 1.

Table 1. Hyperparameter settings for our experiments

6.3. Baselines

To validate our methods for reducing anisotropy, we compared our methods with systems that combine coarse-to-fine antecedent pruning (C2F) (Lee et al., Reference Lee, He and Zettlemoyer2018) with the following HOI modules: AA (Lee et al., Reference Lee, He and Zettlemoyer2018), Entity Equalization (Kantor and Globerson, Reference Kantor and Globerson2019), Span Clustering (Xu and Choi, Reference Xu and Choi2020), and cluster merging (CM) (Xu and Choi, Reference Xu and Choi2020).

We also applied LAIR + DSMS to C2F+SpanBERT+CM, but found this approach did not improve performance and therefore removed the CM module (i.e., LAIR + DSMS + C2F+SpanBERT). This not only could improve performance, but could also significantly accelerate training.

6.4. Results

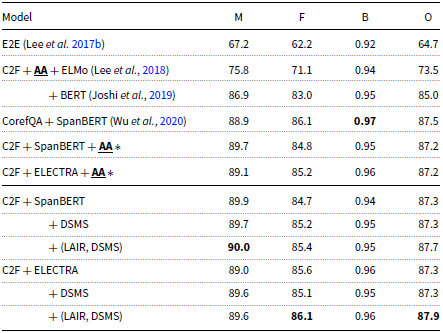
The results on OntoNotes are listed in Table 2. For SpanBERT, (LAIR + DSMS) offers an improvement of + 0.7 F1 over the system that does not use any HOI; the improvement over the system that uses AA is + 1.0 F1. For ELECTRA, (LAIR + DSMS) boosts the performance by + 2.8 F1 over the system that does not use any HOI. The results also show that DSMS alone achieves only marginal improvements without the incorporation of LAIR. We analyze the reasons for this phenomenon in Section 6.5.1.

Table 2. Results on the test set of the OntoNotes English data from the CoNLL-2012 shared task. HOI modules are in bold. The rightmost column is the main evaluation metric, the average F1 of MUC, $B^3$ , $CEAF_{\phi _{4}}$ . BERT, SpanBERT, and ELECTRA are the large model. The results of the models with citations are copied verbatim from the original papers

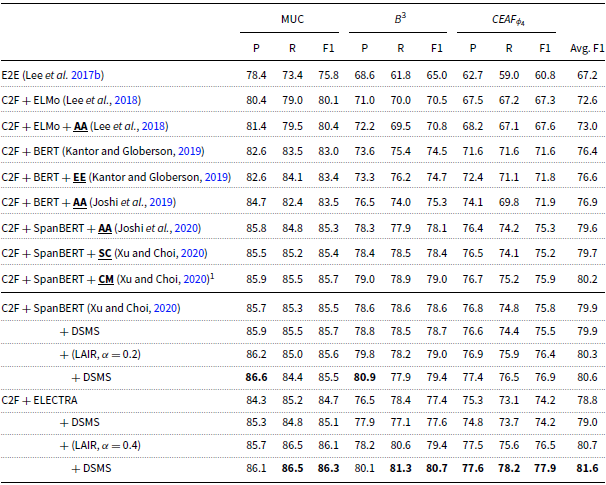
¹ CM is not a span-refinement-based HOI method. The results here are copied verbatim from the original paper. However, we cannot reproduce the reported results (Avg. F1 80.2). When we train “C2F+SpanBERT+CM,” we found the training is extremely slow and can achieve only marginal even negative improvements (Avg. F1 80.0 over 79.9). The marginal improvement of CM is not worth its extreme complexity.

The results on GAP are listed in Table 3. Combined with (LAIR + DSMS), ELECTRA achieves new state-of-the-art for performance on the GAP dataset.

Table 3. Performance on the test set of GAP corpus. The metrics are F1 scores on Masculine and Feminine examples, Overall F1 score, and a Bias factor(F/M). BERT, SpanBERT, and ELECTRA are the large model. The models are trained using OntoNotes and tested on the test set of GAP. $\ast$ denotes the model is re-implemented following Joshi et al. (Reference Joshi, Chen, Liu, Weld, Zettlemoyer and Levy2020)

6.5. Analysis and findings

6.5.1. Effects of LAIR and DSMS

The effects of LAIR and DSMS for learning less-anisotropic span embeddings can be assessed by measuring the degree of anisotropy in those learned span embeddings and relating this to performance. Figure 6 shows the average cosine similarity between randomly sampled spans based on the span embeddings generated by SpanBERT with different settings. The similarities are the measure of anisotropy defined in Equation (10). The less similar the spans are, the less anisotropic are the span embeddings. We can see that LAIR and DSMS effectively reduce the anisotropy of span embeddings. As shown in Table 2 and Figure 6, LAIR + DSMS achieved the best performance with the least anisotropic span embeddings.

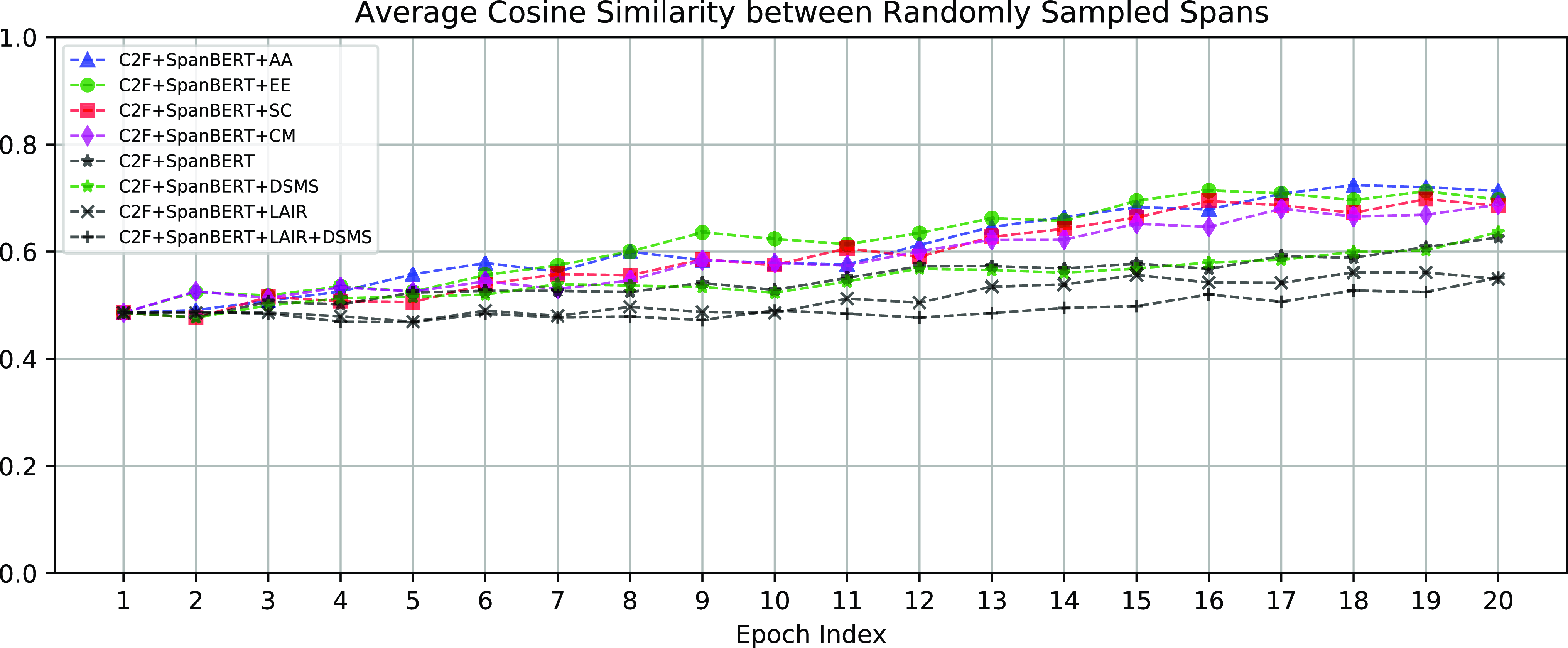
Figure 6. The average cosine similarity between randomly sampled spans. The less similar between spans, the less anisotropic are the span embeddings. LAIR and DSMS help learn less-anisotropic span embeddings.

Case study

We perform a case study on the cosine similarity between The pilots’ and The flight attendants to verify our method further. This is an example in Lee et al. (Reference Lee, He, Lewis and Zettlemoyer2017b) from the OntoNotes dev set (document number: bn/cnn/02/cnn_0210_0). As shown in Figure 7, our LAIR method can effectively make the span embeddings of The pilots’ and The flight attendants less similar, that is less anisotropic.

Figure 7. The cosine similarity between The pilots’ and The flight attendants, an example from OntoNotes dev set.

We find that applying DSMS alone achieves only marginal improvement for both SpanBERT and ELECTRA

As shown in Table 2 ( 11th and 15th rows) and Table 3 (8th and 11th rows), applying solely DSMS can only achieve marginal improvement. Figure 6 shows that DSMS cannot effectively reduce the degree of anisotropy of span embeddings. DSMS is essentially a data augmentation method; training with the augmented examples can only fine-tune span embeddings yet cannot significantly reduce anisotropy (as shown in Figure 6). In contrast, LAIR builds less-anisotropic span embeddings directly by incorporating the embeddings of the bottom layer, that is the least anisotropic layer. Combining DSMS with LAIR can further fine-tune the less-anisotropic span embeddings and improve performances.

We also experimented with less-anisotropic boundary representations, but achieved slightly worse results. This is in line with the fact that the boundary representations were designed to encode a span’s contextual information, while the internal representation was designed to encode the internal information of a span. Replacing first layer embeddings with input layer word embeddings also did not lead to improvement, indicating that the internal representation $\hat{\textbf{g}}_i$ still needs contextual information to better encode a span’s internal structure.

6.5.2. LAIR and DSMS are ineffective for BERT

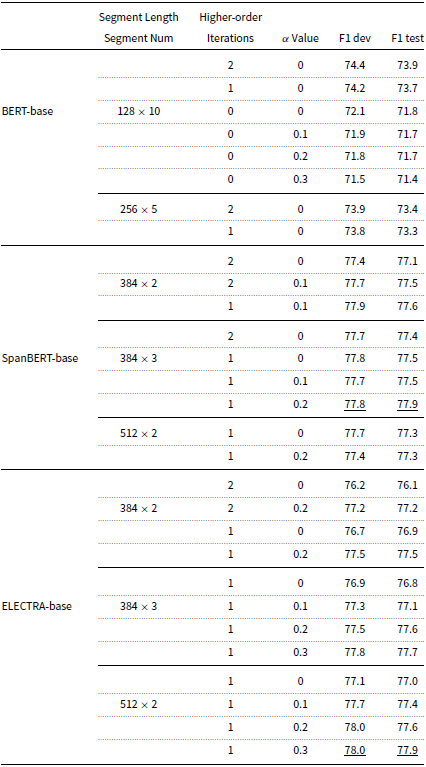
We could not achieve any improvement for BERT by using LAIR or DSMS. The 1st-3rd rows of Table 4 show that decreasing the HOI iterations causes the performance of BERT-base drop significantly. The 3rd-6th rows of Table 4 show that LAIR has negative impact for BERT. BERT has the following two characteristics:

• • The contextualized embeddings from BERT are highly anisotropic. The embeddings of every layer are more anisotropic than those of SpanBERT and ELECTRA, as shown in Figure 3. BERT fine-tuned for coreference resolution becomes even more anisotropic.

• • BERT is not capable of encoding longer contexts effectively (Joshi et al., Reference Joshi, Levy, Zettlemoyer and Weld2019). Figures 4 and 5 also corroborate that BERT-base does not encode sufficient contextual information.

Although LAIR can directly reduce the anisotropy of BERT word embeddings, applying LAIR also depletes the contextual information needed for coreference resolution. Thus, LAIR and DSMS are not effective for BERT.

Table 4. Ablation studies of higher-order inference for BERT-base, ELECTRA-base, and SpanBERT-base. The metric is the average F1 score on the OntoNotes dev set and test set using different combinations of hyperparameters. The HOI method used is the Attended Antecedent Lee et al. (Reference Lee, He and Zettlemoyer2018)

6.5.3. Degree of anisotropy and $\alpha$

Figure 3 shows that the bottom layer is the least anisotropic. This means increasing $\alpha$ (i.e., increasing the proportion of the bottom layer) will make the span embeddings less anisotropic. However, Figures 4 and 5 also show that the bottom layer contains the least contextual information. Thus, increasing $\alpha$ will also deplete the contextual information for coreference resolution. The results in Table 5 show that settings with $\alpha \geq 0.5$ perform poorly. Increasing $\alpha$ worsens performance. Entirely using the bottom layer ( $\alpha =1.0$ ) achieves the worst results.

Table 5. Ablation studies on different $\alpha$ values for different models

As we mentioned in Section 4.4, we need to choose the best $\alpha$ to achieve a trade-off between isotropy and contextualization. According to Figure 3, ELECTRA is more anisotropic than SpanBERT. In Table 2, the 11th and 14th rows show that LAIR performs the best when $\alpha$ is set to 0.2 for SpanBERT and 0.4 for ELECTRA, respectively. We can say that the more anisotropic the embeddings are, larger the $\alpha$ (Equation 14) is needed for LAIR.