Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-09T20:36:51.906Z Has data issue: false hasContentIssue false
  • English
  • Français

A randomised inference algorithm for regular tree languages

Published online by Cambridge University Press:  21 March 2011

JOHANNA HÖGBERG
JOHANNA HÖGBERG*
Affiliation:
Department of Computing Science, Umeå University, SE–901 87 Umeå, Sweden email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a randomised inference algorithm for regular tree languages. The algorithm takes as input two disjoint finite nonempty sets of trees 𝒫 and 𝒩 and outputs a nondeterministic finite tree automaton that accepts every tree in 𝒫 and rejects every tree in 𝒩. The output automaton typically represents a nontrivial generalisation of the examples given in 𝒫 and 𝒩. To obtain compact output automata, we use a heuristics similar to bisimulation minimisation. The algorithm has time complexity of 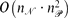, where n𝒩 and n𝒫 are the size of 𝒩 and 𝒫, respectively. Experiments are conducted on a prototype implementation, and the empirical results appear to second the theoretical results.

Type
Papers
Information
Natural Language Engineering , Volume 17 , Special Issue 2: Finite-State Methods and Models in Natural Language Processing , April 2011 , pp. 203 - 219
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adriaans, P. 1999. Learning shallow context-free languages under simple distributions. Technical Report PP-1999-13, Institute for Logic, Language, and Computation, Amsterdam.Google Scholar
Adriaans, P., Trautwein, M. and Vervoort, M. 2000. Towards high speed grammar induction on large text corpora. In Proceedings of the 27th Annual Conference on Current Trends in Theory and Practice of Informatics, Volume 1963 of LNCS, Milovy, Czech Republic, pp. 173–86. 0.501961,1,1Berlin/Heidelberg, Germany: Springer-Verlag.Google Scholar
Angluin, D. 1981. A note on the number of queries needed to identify regular languages. Information and Computation 51: 76–87.Google Scholar
Angluin, D. 1987. Learning regular sets from queries and counterexamples. Information and Computation 75: 87–106.CrossRefGoogle Scholar
Besombes, J. and Marion, J. 2007. Learning tree languages from positive examples and membership queries. Theoretical Computer Science 382: 183–97.CrossRefGoogle Scholar
Bod, R. 1999. Extracting stochastic grammars from treebanks. In Delmonte, R. (ed.), Proceedings of Venezia per il Trattamente Automatico delle Lingue, Venice, Italy, pp. 229–34. Padova, Italy: Unipress.Google Scholar
Buchholz, P. 2008. Bisimulation relations for weighted automata. Theoretical Computer Science 393 (1–3): 109–23.CrossRefGoogle Scholar
Clark, A. and Eyraud, R. 2005. Identification in the limit of substitutable context-free languages. In Jain, S., Simon, H., and Tomita, E. (eds.), Proceedings of the 16th International Conference on Algorithmic Learning Theory, Volume 3734 of LNAI, Singapore, pp. 283–96. Berlin/Heidelberg, Germany: Springer-Verlag.Google Scholar
Comon, H., Dauchet, M., Gilleron, R., Jacquemard, F., Lugiez, D., Tison, S., and Tommasi, M. 1997. Tree automata techniques and applications. Resource location. http://www.grappa.univ-lille3.fr/tata. Accessed October 26th, 2010.Google Scholar
Coste, F. and Fredouille, D. 2003. Unambiguous automata inference by means of state-merging methods. In Lavrac, N., Gamberger, D., Todorovski, L., and Blockeel, H. (eds.), Proceedings of the European Conference on Machine Learning, Volume 2837 of LNCS, Cavtat-Dubrovnik, Croatia, pp. 60–71. Berlin/Heidelberg, Germany: Springer-Verlag.Google Scholar
Denis, F., Lemay, A. and Terlutte, A. 2000. Learning regular languages using non deterministic finite automata. In Oliveira, A. L. (ed.), Proceedings of the 5th International Conference on Grammatical Inference: Algorithms and Applications, Volume 1891 of LNCS, Lisbon, Portugal, pp. 39–50. Berlin/Heidelberg, Germany: Springer-Verlag.CrossRefGoogle Scholar
Denis, F., Lemay, A. and Terlutte, A. 2001. Residual finite state automata. In Ferreira, A., and Reichel, H. (eds.), Proceedings of the 18th Annual Symposium on Theoretical Aspects of Computer Science, Volume 2010 of LNCS, pp. 144–57. Berlin/Heidelberg, Germany: Springer 0.501961,1,1-Verlag.Google Scholar
de Parga, M. V., García, P., and Ruiz, J. 2006. A family of algorithms for non deterministic regular languages inference. In Ibarra, O., and Yen, H. (eds.), Proceedings of the 11th International Conference on Implementation and Application of Automata, Volume 4094 of LNCS, pp. 265–74. Berlin/Heidelberg, Germany: Springer-Verlag.CrossRefGoogle Scholar
Drewes, F. 2009. MAT learners for recognizable tree languages and tree series. Acta Cybernetica 19 (2): 249–74.Google Scholar
Drewes, F. and Högberg, J. 2007. Query learning of regular tree languages: how to avoid dead states. Theory of Computing Systems 40: 163–85.CrossRefGoogle Scholar
Drewes, F. and Vogler, H. 2007. Learning deterministically recognizable tree series. Journal of Automata, Languages and Combinatorics 12 (3): 333–54.Google Scholar
Edelman, S., Solan, Z., Horn, D. and Ruppin, E. 2005. Learning syntactic constructions from raw corpora. In Brugo, A., Clark-Cotton, M., and Ha, S. (eds.), Proceedings of the 29th Boston University Conference on Language Development. MA, USA: Boston University.Google Scholar
García, P., de Parga, M., Álvarez, G., and Ruiz, J. 2008. Learning regular languages using nondeterministic finite automata. In Ibarra, O., and Ravikumar, B. (eds.), Conference on Implementation and Application of Automata, Volume 5148 of LNCS, San Francisco, California, pp. 92–101. Berlin/Heidelberg, Germany: Springer 0.501961,1,1-Verlag.CrossRefGoogle Scholar
Garcia, P. and Oncina, J. 1993. Inference of recognizable tree sets. Technical Report DSIC-II/47/93, Universidad Politecnica de Valencia, Valencia, Spain.Google Scholar
Geertzen, J. and van Zaanen, M. 2004. Grammatical inference using suffix trees. In Paliouras, G., and Sakakibara, Y. (eds.), Proceedings of the 7th International Conference on Grammatical Inference: Algorithms and Applications, Volume 3264 of LNCS, Athens, Greece. Berlin/Heidelberg, Germany: Springer-Verlag.Google Scholar
Gold, E. M. 1967. Language identification in the limit. Information and Control 10 (5): 447–74.CrossRefGoogle Scholar
Gold, E. M. 1978. Complexity of automaton identification from given data. Information and Control 37 (3): 302–20.CrossRefGoogle Scholar
Habrard, A. and Oncina, J. 2006. Learning multiplicity tree automata. In Sakakibara, Y., Kobayashi, S., Sato, K., Nishino, T., and Tomita, E. (eds.), Proceedings of the 8th International Colloquium on Grammatical Inference: Algorithms and Applications, Volume 4201 of LNCS, Tokyo, Japan, pp. 268–80. Berlin/Heidelberg, Germany: Springer-Verlag.CrossRefGoogle Scholar
Harris, Z. S. 1951. Methods in Structural Linguistics. Chicago, IL, USA: University of Chicago Press.Google Scholar
Knight, K. and May, J. 2009. Applications of weighted automata in natural language processing. In Droste, M., Kuich, W., and Vogler, H. (eds.), Handbook of Weighted Automata. Berlin/Heidelberg, Germany: Springer-Verlag.Google Scholar
Lang, K., Pearlmutter, B. and Price, R. 1998. Results of the Abbadingo one DFA learning competition and a new evidence-driven state merging algorithm. In Honavar, V., and Slutzki, G. (eds.), Proceedings of the 4th International Colloquium on Grammatical Inference: Algorithms and Applications, Ames, Iowa, Volume 1433 of LNCS, pp. 1–12. Berlin/Heidelberg, Germany: Springer-Verlag.Google Scholar
Maletti, A. 2007. Learning deterministically recognizable tree series — revisited. In Bozapalidis, S., and Rahonis, G. (eds.), Conference on Algebraic Informatics, Volume 4728 of LNCS, Thessaloniki, Greece, pp. 218–35. Berlin/Heidelberg, Germany: Springer-Verlag.CrossRefGoogle Scholar
Oncina, J. and Garcia, P. 1991. Inferring regular languages in polynomial update time. In de la Blanca, N. P., Sanfeliu, A., and Vidal, E. (eds.), Pattern Recognition and Image Analysis, pp. 49–61. Singapore: World Scientific.Google Scholar
Pitt, L. and Warmuth, M. 1989. The minimum consistent DFA problem cannot be approximated within any polynomial. In Proceedings of the 21st Annual ACM Symposium on Theory of Computing, MA, USA. ACM, pp. 421–32.Google Scholar
Russell, S. J. and Norvig, P. 2003. Artificial Intelligence: A Modern Approach, 2nd ed.NJ, USA: Prentice Hall.Google Scholar
Sakakibara, Y. and Muramatsu, H. 2000. Learning context-free grammars from partially structured examples. In Oliveira, A. L. (ed.), Proceedings of the 5th International Conference on Grammatical Inference: Algorithms and Applications, Volume 1891 of LNCS, Lisbon, Portugal, pp. 229–40. Berlin/Heidelberg, Germany: Springer-Verlag.CrossRefGoogle Scholar
Schmidt, E. M. 1978. Succinctness of Description of Context-Free, Regular and Unambiguous Languages. PhD thesis. Cornell University, Ithaca, New York.CrossRefGoogle Scholar
Trakhtenbrot, B. and Barzdin, Y. 1973. Finite Automata: Behavior and Synthesis, Volume 1 of FSCS. Amsterdam, North-Holland: Elsevier. Translated from Russian by Louvish, D..Google Scholar
van Zaanen, M. 2001. Bootstrapping Structure into Language: Alignment-Based Learning. PhD thesis. School of Computing, University of Leeds, Leeds, UK.Google Scholar