In this note it is shown that Schläfli function can be simply expressed in terms of hyperlogarithmic functions, namely iterated integrals of forms with logarithmic poles in the sense of K. T. Chen (Theorem 1). It is also discussed the relation between Schläfli function and hypergeometric ones of Mellin-Sato type (Theorem 2). From a combinatorial point of view the structure of hyperlogarithmic functions seem very interesting just as the dilog log (so-called Abel-Rogers function) has played a crucial part in Gelfand-Gabriev-Losik’s formula of 1st Pontrjagin classes. See also [3].

Consider an algebraic differential equation F = 0 of the first order. A rigorous definition will be given to the classical concept of “particular solutions” of F = 0. By Ritt’s low power theorem we shall prove that a singular solution of F = 0 belongs to the general solution of F if and only if it is a particular solution of F = 0.

It has often been pointed out that a much more manageable structure is obtained from quantum theory if the time parameter t is chosen imaginary instead of real. Under a replacement of t by i·t the Schrödinger equation turns into a generalized heat equation, time ordered correlation functions transform into the moments of a probability measure, etc. More recently this observation has become extremely important for the construction of quantum dynamical models, where criteria were developed by E. Nelson, by K. Osterwalder and R. Schrader and others [8] which would permit the reverse transition to real time after one has constructed an imaginary time (“Euclidean”) model.

The exponential decay of the local energy for wave equations in exterior domains of the odd dimensional space has been proved in [1] ~ [6] etc. under the Dirichlet boundary condition and in [5], [7] under the Neumann condition and the other conditions. In this paper, we shall consider this problem for the following equation:

One purpose of this paper is a purely algebraic study of (systems of) ordinary differential equations of the type

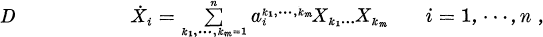
where the coefficients are taken from a fixed associative, commutative, unital ring R, such as the field R of real or C of complex numbers or a commutative, unital Banach algebra. The right hand sides of D are considered to be elements in the polynomial ring R[X1, …, Xn] of associating but non-commuting variables X1, …, Xn. An algebraic study calls for maps between such differential equations and, in fact, morphisms are defined between differential equations having the same arity m but not necessarily the same dimension n. These morphisms are rectangular matrices with entries in R which satisfy certain relations. This leads to a category RDiffm whose objects are precisely the differential equations of arity m and in which the composition of the morphisms is the usual matrix multiplication.

In this note we will make a few observations on the structure of fields and local rings. The main point is to show that a weaker version of Cohen structure theorem for complete local rings holds for any (not necessarily complete) local ring. The consideration of non-complete case makes the meaning of Cohen’s theorem itself clearer. Moreover, quasi-coefficient fields (or rings) are handy when we consider derivations of a local ring.