Research Article
Structure of solutions to Fuchsian systems of partial differential equations
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-17
-
- Article
-
- You have access
- Export citation
Singular invariant hyperfunctions on the square matrix space and the alternating matrix space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 19-75
-
- Article
-
- You have access
- Export citation
Modification of balayage spaces by transitions with application to coupling of PDE’s
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 77-118
-
- Article
-
- You have access
- Export citation
On the rational solutions of q-Painlevé V equation
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 119-143
-
- Article
-
- You have access
- Export citation
Algebraic dependence of meromorphic mappings in value distribution theory
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-178
-
- Article
-
- You have access
- Export citation
An application of Iwasawa theory to constructing fields Q(ζn +
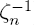 ) which have class group with large p-rank
) which have class group with large p-rank
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 179-190
-
- Article
-
- You have access
- Export citation
Invariant Kähler structures on the cotangent bundles of compact symmetric spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 191-217
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 169 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f3
-
- Article
-
- You have access
- Export citation

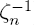 ) which have class group with large
) which have class group with large