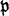Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T00:06:32.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Vertices of ideals of a -adic number field II

Published online by Cambridge University Press:  22 January 2016

Yoshimasa Miyata
Yoshimasa Miyata*
Affiliation:
Faculty of Education Shizuoka University Shizuoka, 422 Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be a 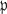-adic number field with the ring 0 of all integers in k, and K be a finite normal extension with Galois group G. ∏ denotes a prime element of the ring 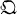of all integers in K. Then, an ideal (∏a) of 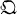is an 0G-module. E. Noether showed that if K/k is tamely ramified, 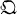is a free 0G-module. A. Fröhlich generalized E. Noether’s theorem as follows: 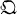is relatively projective with respect to a subgroup S of G if and only if S ⊇ G1 where G1 is the first ramification group of K/k. Now we define the vertex V(∏a) of (∏a) as the minimal normal subgroup S of G such that (∏a) is relatively projective with respect to a subgroup S of G (cf. § 1). Then, the above generalization by A. Fröhlich implies V(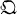) = G1. In the previous paper, we proved G1 ⊇ V(∏a) ⊇ G2, (where G2 is the second ramification group of K/k (cf. Theorem 5). Further, we dealt with the case where G = G1 is of order p2, and proved that if V(∏a) ≠ G1 then a ≡ 1(p2) and t2 ≡ 1(p2) for the second ramification number t2 of K/k (cf. Theorems 15 and 21). The purpose of this paper is to prove the similar theorem for the wildly ramified p-extension of degree pn (Theorem 7).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 107 , September 1987 , pp. 49 - 62
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1987

References

[1] Curtis, C. W. and Reiner, I., Methods of Representation Theory Vol. 1, Interscience, New York, 1981.Google Scholar
[2] Fröhlich, A., Some topics in the theory of module conductors, Oberwolfach Berichte, 2 (1966), 59–83.Google Scholar
[3] Hasse, H., Führer, Discriminant und Verzweigungskörper relative-Abelscher Zahlkörper, J. reine angew. Math., 162 (1930), 169–184.Google Scholar
[4] Huppert, B., Endliche Gruppen I, Springer-Verlag, Berlin, 1967.CrossRefGoogle Scholar
[5] Noether, E., Normalbasis bei Körpern ohne höhere Verzweigung, J. reine angew. Math., 167 (1932), 147–152.Google Scholar
[6] Miyata, Y., On the module structure of the ring of all integers of a p-adic number field, Nagoya Math. J., 54 (1974), 53–59.Google Scholar
[7] Miyata, Y., Vertices of ideals of a p-adic number field, Illinois J. Math., to appear.Google Scholar
[8] Serre, J. P., Corps Locaux, Hermann, Paris, 1968.Google Scholar
[9] Vostokov, S. V., Ideals of an abelian p-extension of an irregular local field as Galois modules, Zap. Nauchn. Sem. Leningrad. Otdel. Math. Inst. Steklov. (LOMI), 46 (1974), 14–35 (Russian).Google Scholar
[10] Vostokov, S. V., Ideals of an abelian p-extension of a local field as Galois modules, Zap. Nauchn. Sem. Leningrad. Otdel. Math. Inst. Steklov. (LOMI), 57 (1976), 64–84 (Russian).Google Scholar