Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T23:11:24.543Z Has data issue: false hasContentIssue false
  • English
  • Français

Vector Field Energies and Critical Metrics on Kähler Manifolds

Published online by Cambridge University Press:  22 January 2016

Toshiki Mabuchi
Toshiki Mabuchi*
Affiliation:
Department of Mathematics, Osaka University, Toyonaka, Osaka, 560-0043, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Associated with a Hamiltonian holomorphic vector field on a compact Kähler manifold, a nice functional on a space of Kähler metrics will be constructed as an integration of the bilinear pairing in [FM] contracted with the Hamiltonian holomorphic vector field. As applications, we have functionals 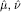whose critical points are extremal Kähler metrics or “Kähler-Einstein metrics” in the sense of [M4], respectively. Finally, the same method as used by [G1] allows us to obtain, from the convexity of 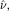, the uniqueness of “Kähler-Einstein metrics” on nonsingular toric Fano varieties possibly with nonvanishing Futaki character.

Keywords

53C5514J4514J5032J25
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 162 , June 2001 , pp. 41 - 63
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2001

References

[BM1] Bando, S. and Mabuchi, T., On some integral invariants on complex manifolds I, Proc. Japan Acad., 62 (1986), 197–200.Google Scholar
[BM2] Bando, S. and Mabuchi, T., Uniqueness of Einstein Kähler metrics modulo connected group actions, Algebraic Geometry, Sendai, 1985, Adv. Stud. Pure Math. 10, Kinokuniya and North-Holland, Tokyo and Amsterdam (1987), pp. 11–40.Google Scholar
[C1] Calabi, E., Extremal Kähler metrics II, Differential geometry and complex analysis (Chaveland, I. Farkas, H.M., eds.), Springer-Verlag, Heidelberg (1985), pp. 95–114.Google Scholar
[D1] Ding, W., Remarks on the existence problem of positive Kähler-Einstein metrics, Math. Ann., 282 (1988), 463–471.CrossRefGoogle Scholar
[DT] Ding, W. and Tian, G., The generalized Moser-Truginger inequality, Proc. Nankai Internat. Conf. Nonlinear Analysis (1993).Google Scholar
[Fj] Fujiki, A., On automorphism groups of compact Kähler manifolds, Invent. Math., 44 (1978), 225–258.Google Scholar
[F1] Futaki, A., An obstruction to the existence of Einstein Kähler metrics, Invent. Math., 73 (1983), 437–443.Google Scholar
[F2] Futaki, A., Kähler-Einstein metrics and integral invariants, Lect. Notes in Math. 1314, Springer-Verlag, Heidelberg, 1988.Google Scholar
[FM] Futaki, A. and Mabuchi, T., Bilinear forms and extremal Kähler vector fields associated with Kähler classes, Math. Ann., 301 (1995), 199–210.Google Scholar
[G1] Guan, Z.D., On modified Mabuchi functional and Mabuchi moduli space of Kähler metrics on toric bundles, Math. Res. Letters, 6 (1999), 547–555.CrossRefGoogle Scholar
[GC] Guan, Z.D. and Chen, X., Existence of extremal metrics on almost homogeneous manifolds of cohomogeneity one, to appear in Asian J. Math.,Google Scholar
[LS] LeBrun, C. and Simanca, S., Extremal Kähler metrics and complex deformation theory, Geom. Funct. Anal., 4 (1994), 298–336.Google Scholar
[M1] Mabuchi, T., K-energy maps integrating Futaki invariants, Tôhoku Math. J., 38 (1986), 575–593.CrossRefGoogle Scholar
[M2] Mabuchi, T., Some symplectic geometry on compact Kähler manifolds (I), Osaka J. Math., 24 (1987), 227–252.Google Scholar
[M3] Mabuchi, T., An algebraic character associated with Poisson brackets, Recent topics in differential and analytic geometry, Adv. Stud. Pure Math. 18-I, Kinokuniya and Academic Press, Tokyo and New York (1990), pp. 339–358.Google Scholar
[M4] Mabuchi, T., Kähler-Einstein metrics for manifolds with nonvanishing Futaki character, to appear in Tôhoku Math. J., 53 (2001).Google Scholar
[M5] Mabuchi, T., Multiplier Hermitian structures on Kähler manifolds, preprint.Google Scholar
[N1] Nakagawa, Y., Bando-Calabi-Futaki characters of Kähler orbifolds, Math. Ann., 314 (1999), 369–380.CrossRefGoogle Scholar
[S1] Simanca, S., A K-energy characterization of extremal Kähler metrics, Proc. Amer. Math. Soc, 128 (2000), 1531–1535.Google Scholar