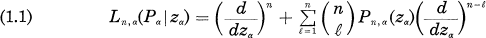Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T23:24:52.166Z Has data issue: false hasContentIssue false
  • English
  • Français

The variational theory of higher-order linear differential equations

Published online by Cambridge University Press:  22 January 2016

Yasuo Teranishi
Yasuo Teranishi*
Affiliation:
Department of Mathematics Faculty of Science, Nagoya University, Chikusa-ku, Nagoya 464, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In his paper [2], [3], D. A. Hejhal investigated the variational theory of linear polynomic functions. In this paper we are concerned with the variational theory of higher-order differential equations. To be more precise, consider a compact Riemann surface having genus g > 1. As is well known, we can choose a projective coordinate covering U = (Ua, za). Fix this coordinate covering of X. We shall be concerned with linear ordinary differential operators of order n defined in each projective coordinate open set Ua

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 95 , September 1984 , pp. 137 - 161
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1984

References

[ 1 ] Morikawa, H., Some analytic and geometric applications of the invariant theoretic method, Nagoya Math. J., 80 (1980), 1–47.Google Scholar
[ 2 ] Hejhal, D.A., The variational theory of linearly polynomic functions, J. Analyse Math., 30 (1976), 215–264.CrossRefGoogle Scholar
[ 3 ] Hejhal, D.A., Monodromy groups and Poincaré series, Bull. Amer. Math. Soc, 84 (1978), 339–376.Google Scholar
[ 4 ] Gunning, R.C., Lectures on Riemann Surfaces, Princeton Univ. Press, (Mathematical Notes 2), 1966.Google Scholar
[ 5 ] Gunning, R.C., Analytic structures on the space of flat vector bundles over a compact Riemann surface, Several Complex Variables II, Maryland, 1970. Springer Lecture Notes 185 (1971), 47–62.Google Scholar
[ 6 ] Gunning, R.C., Lectures on Vector Bundles over Riemann Surfaces, Princeton University Press, 1967.Google Scholar