Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T23:15:26.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Units and Cyclotomic Units in Zp-Extensions

Published online by Cambridge University Press:  22 January 2016

Jae Moon Kim
Jae Moon Kim*
Affiliation:
Department of Mathematics, Inha University, Inchon, Korea (e-mail) [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p be an odd prime and d be a positive integer prime to p such that d ≢ 2 mod 4. For technical reasons, we also assume that 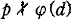. For each integer n ≥ 1, we choose a primitive nth root ζn of 1 so that 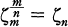whenever n | m. Let 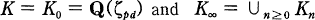be its cyclotomic Zp-extension, where 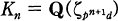is the nth layer of this extension. For n ≤ 1, we denote the Galois group Ga\(Kn/K0) by Gn, the unit group of the ring of integers of Kn by En, and the group of cyclotomic units of Kn by Cn. For the definition and basic properties of cyclotomic units such as the index theorem, we refer [6] and [7]. In this paper we examine the injectivity of the homomorphism 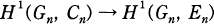between the first cohomology groups induced by the inclusion Cn → En.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 140 , December 1995 , pp. 101 - 116
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[ 1 ] Ennola, V., On relations between cyclotomic units, J. Number Theory, 4 (1972), 236–247.Google Scholar
[2] Gold, R., Kim, J. M., Bases for cyclotomic units, Compositio Math., 71 (1989), 13–28.Google Scholar
[ 3 ] Iwasawa, K., On Cohomology groups of units for Zp-extensions, Amer. J. Math., 105 No.1 (1983), 189–200.Google Scholar
[4] Kim, J. M., Cohomology groups of cyclotomic units, J. Algebra, 152, no.2 (1992), 514–519.Google Scholar
[ 5 ] Kim, J. M., Coates-Wiles series and Mirimanoff’s polynomial, J. Number Theory, 54, No.2 (1995), 173–179.Google Scholar
[ 6 ] Sinnott, W., On the Stickelberger ideal and the circular units of a cyclotomic field, Ann. of Math., (2) 108 (1978), 107–134.CrossRefGoogle Scholar
[ 7 ] Washington, L., Introduction to Cyclotomic Fields, G. T. M., Springer-Verlag, New York, 1980.Google Scholar