Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lagarias, J. C.
1980.
On the computational complexity of determining the solvability or unsolvability of the equation 𝑋²-𝐷𝑌²=-1.
Transactions of the American Mathematical Society,
Vol. 260,
Issue. 2,
p.
485.


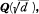 let (x,y) = (t,u) be the least positive integral solution of Pell’s equation x
let (x,y) = (t,u) be the least positive integral solution of Pell’s equation x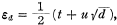 and denote by h
and denote by h