Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saad, Hedi Ben
and
Janßen, Klaus
1990.
Bernsteins theorem for completely excessive measures.
Nagoya Mathematical Journal,
Vol. 119,
Issue. ,
p.
133.
Steffens, J.
1992.
Duality and integral representation for excessive measures.
Mathematische Zeitschrift,
Vol. 210,
Issue. 1,
p.
495.
Janssen, K.
1994.
Choquet-type integral representation of polysupermedian measures.
Potential Analysis,
Vol. 3,
Issue. 4,
p.
359.
Janßen, Klaus
and
Müller, Hans-Helge
1994.
Classical and Modern Potential Theory and Applications.
p.
293.
Hirsch, Francis
and
Yor, Marc
2012.
On temporally completely monotone functions for Markov processes.
Probability Surveys,
Vol. 9,
Issue. none,


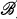 ) be a measurable space and
) be a measurable space and 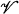 be a submarkovian resolvent of kernels (with the initial kernel
be a submarkovian resolvent of kernels (with the initial kernel 