Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kubota, Tomio
1956.
Über Den Bizyklischen Biquadratischen Zahlkörper.
Nagoya Mathematical Journal,
Vol. 10,
Issue. ,
p.
65.
Halter-Koch, Franz
1972.
Ein Satz über die Geschlechter relativ-zyklischer Zahlkörper von Primzahlgrad und seine Anwendung auf biquadratisch-bizyklische Körper.
Journal of Number Theory,
Vol. 4,
Issue. 2,
p.
144.
1975.
The Theory of Numbers.
Vol. 8,
Issue. ,
p.
519.
Parry, Charles J.
1977.
Real quadratic fields with class numbers divisible by five.
Mathematics of Computation,
Vol. 31,
Issue. 140,
p.
1019.
Buell, D. A.
Williams, H. C.
and
Williams, K. S.
1977.
On the imaginary bicyclic biquadratic fields with class-number 2.
Mathematics of Computation,
Vol. 31,
Issue. 140,
p.
1034.
Parry, Charles J.
1978.
On the class number of relative quadratic fields.
Mathematics of Computation,
Vol. 32,
Issue. 144,
p.
1261.
Setzer, C.Bennett
1980.
Units over totally real C2 × C2 fields.
Journal of Number Theory,
Vol. 12,
Issue. 2,
p.
160.
Hirabayashi, Mikihito
and
Yoshino, Ken-ichi
1989.
Remarks on unit indices of imaginary abelian number fields II.
Manuscripta Mathematica,
Vol. 64,
Issue. 2,
p.
235.
Hirabayashi, Mikihito
and
Yoshino, Ken-ichi
1990.
Unit indices of imaginary abelian number fields of type (2, 2, 2).
Journal of Number Theory,
Vol. 34,
Issue. 3,
p.
346.
Bond, Robert J
1992.
On the splitting of the Hilbert class field.
Journal of Number Theory,
Vol. 42,
Issue. 3,
p.
349.
Berger, Ruth I.
1992.
Hasse's class number product formula for generalized Dirichlet fields and other types of number fields.
Manuscripta Mathematica,
Vol. 76,
Issue. 1,
p.
397.
Louboutin, Stéphane
1994.
On the class number one problem for nonnormal quartic {CM}-fields.
Tohoku Mathematical Journal,
Vol. 46,
Issue. 1,
Levesque, C.
and
Lu, H.
1996.
On S. Chowla's conjecture.
Acta Mathematica Hungarica,
Vol. 70,
Issue. 3,
p.
237.
Azizi
and
Abdelmalek
1999.
Algebra And Number Theory.
Azizi, Abdelmalek
1999.
Sur le 2-groupe de classes d'idéaux de ℚ(√d,i).
Rendiconti del Circolo Matematico di Palermo,
Vol. 48,
Issue. 1,
p.
71.
Benjamin, Elliot
Lemmermeyer, Franz
and
Snyder, Chip
2007.
On the unit group of some multiquadratic number fields.
Pacific Journal of Mathematics,
Vol. 230,
Issue. 1,
p.
27.
GÓMEZ-MOLLEDA, M. A.
and
LARIO, JOAN-C.
2012.
CLASS NUMBER FORMULAS FOR CERTAIN BICYCLIC BIQUADRATIC NUMBER FIELDS AS FINITE SUMS INVOLVING JACOBI ELLIPTIC FUNCTIONS.
International Journal of Number Theory,
Vol. 08,
Issue. 05,
p.
1257.
Azizi, Abdelmalek
Talbi, Mohamed
Talbi, Mohammed
Derhem, Aïssa
and
Mayer, Daniel C.
2016.
The group Gal(k3(2)|k) for k = ℚ(−3,d) of type (3,3).
International Journal of Number Theory,
Vol. 12,
Issue. 07,
p.
1951.
Umegaki, Atsuki
and
Umegaki, Yumiko
2020.
Quartic fields with large class numbers.
Rocky Mountain Journal of Mathematics,
Vol. 50,
Issue. 1,
Chan, Stephanie
and
Milovic, Djordjo
2022.
Kuroda’s formula and arithmetic statistics.
Mathematische Zeitschrift,
Vol. 300,
Issue. 2,
p.
1509.
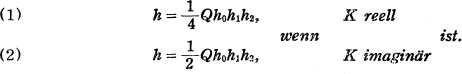
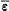 , welche von der Einheiten von ki (i = 0, 1, 2) erzeugt wird, in der vollen Gruppe der Einheiten E von K: d.h.
, welche von der Einheiten von ki (i = 0, 1, 2) erzeugt wird, in der vollen Gruppe der Einheiten E von K: d.h. 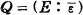 .
.

