Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T23:30:59.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Transforms on white noise functionals with their applications to Cauchy problems

Published online by Cambridge University Press:  22 January 2016

Dong Myung Chung  and
Un Cig Ji
Dong Myung Chung
Affiliation:
Department of Mathematics, Sogang University, Seoul, 121-742, [email protected]
Un Cig Ji
Affiliation:
Department of Mathematics, Sogang University, Seoul, 121-742, Korea
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

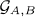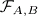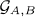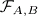A generalized Laplacian ΔG(K) is defined as a continuous linear operator acting on the space of test white noise functionals. Operator-parameter - and -transforms on white noise functionals are introduced and then prove a characterization theorem for and -transforms in terms of the coordinate differential operator and the coordinate multiplication. As an application, we investigate the existence and uniqueness of solution of the Cauchy problem for the heat equation associated with ΔG(K)

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 147 , September 1997 , pp. 1 - 23
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1997

References

[1] Chung, D. M. and Ji, U. C., Transformation groups on white noise junctionals and their applications, to appear, Appl. Math. Opt..Google Scholar
[2] Chung, D. M. and Ji, U. C., Some Cauchy problems in white noise analysis and associated semigroups of operators, to appear, Stoch. Anal. Appl..Google Scholar
[3] Chung, D. M., Ji, U. C. and Obata, N., Transformations on white noise functions associated with second order differential operators of diagonal type, to appear, Nagoya Math. J..Google Scholar
[4] Dôku, I., Kuo, H.-H. and Lee, Y. J., Fourier transform and heat equation in white noise analysis, Stochastic analysis on infinite dimensional space (Kunita, H. and Kuo, H.-H., eds.), Pitman Research Notes in Mathematics Series 310, Logman Scientific & Technical, pp. 60–74.Google Scholar
[5] Gross, L., Potential theory on Hilbert space, J. Funct. Anal., 1, 123–181.CrossRefGoogle Scholar
[6] Hida, T., Obata, N. and Saitô, K., Infinite dimensional rotations and Laplacians in terms of white noise calculus, Nagoya Math. J., 128, 65–93.Google Scholar
[7] Hida, T., Kuo, H.-H. and Obata, N., Transformations for white noise functionals, J. Funct. Anal., 111, 259–277.Google Scholar
[8] Hida, T., Kuo, H.-H., Potthoff, J. and Streit, L. (eds.), White noise: An Infinite Dimensional Calculus, Kluwer Academic Publishers.Google Scholar
[9] Kubo, I. and Yokoi, Y., A remark on the space of testing random variables in the white noise calculus, Nagoya Math. J., 115, 139–149.Google Scholar
[10] Kuo, H.-H., Gaussian Measures in Banach Space, Lect. Notes in Math., 463, Springer-Verlag, Berlin/Heidelberg/New York.Google Scholar
[11] Kuo, H.-H., On Laplacian operators of generalized Brownian functionals, Stochastic Processes and Applications (Itô, K. and Hida, T., eds.), Lect. Notes in Math., 1203, Springer-Verlag, pp. 119-128.Google Scholar
[12] Kuo, H.-H., Fourier transform in white noise calculus, J. Multivar. Anal., 31, 311–327.CrossRefGoogle Scholar
[13] Kuo, H.-H., Fourier-Mehler transform in white noise analysis, Gaussian Random Fields (K. Ito and T. Hida, eds.), the third Nagoya Lévy Seminar, World Scientific, Singapore/New Jersey, pp. 257–271.Google Scholar
[14] Kuo, H.-H., Lectures on white noise analysis, Soochow J. Math., 18, 229–300.Google Scholar
[15] Lee, Y.-J., Applications of the Fourier-Wiener transform to differential equations on infinite dimensional space I, Trans. Amer. Math. Soc, 262, 259–283.Google Scholar
[16] Lee, Y.-J., Integral transforms of analytic functions on abstract Wiener spaces, J. Funct. Anal., 47, 153–164.Google Scholar
[17] Obata, N., An analytic characterization of symbols of operators on white noise junctionals, J. Math. Soc. Japan, 45, 421–445.Google Scholar
[18] Obata, N., White noise calculus and Fock space, Lecture Notes in Math, 1577, Springer-Verlag, Berlin/Heidelberg/New York.Google Scholar
[19] Piech, M.A., A fundamental solution of the Parabolic equation on Hilbert space, J. Funct. Anal, 3, 85–114.Google Scholar
[20] Potthoff, J. and Streit, L., A characterization of Hida distributions, J. Funct. Anal., 101, 212–229.CrossRefGoogle Scholar
[21] Potthoff, J. and Yan, J.-A., Some results about test and generalized junctionals of white noise, Proc. Singapore Probab. Conf. 1989 (Chen, L. Y., ed.), Walter de Gruyter, Berlin/New York, pp. 121–145.Google Scholar