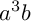Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T13:49:49.944Z Has data issue: false hasContentIssue false
  • English
  • Français

TILINGS OF THE SPHERE BY CONGRUENT QUADRILATERALS II: EDGE COMBINATION $a^3b$ WITH RATIONAL ANGLES

Part of: Discrete geometry Designs and configurations

Published online by Cambridge University Press:  07 September 2023

YIXI LIAO Open the ORCID record for YIXI LIAO [Opens in a new window]  and
ERXIAO WANG Open the ORCID record for ERXIAO WANG [Opens in a new window]
YIXI LIAO
Affiliation:
School of Mathematical Sciences Zhejiang Normal University 688 Yingbin Road Jinhua, Zhejiang Province, 321004 China [email protected]
ERXIAO WANG*
Affiliation:
School of Mathematical Sciences Zhejiang Normal University 688 Yingbin Road Jinhua, Zhejiang Province, 321004 China
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Edge-to-edge tilings of the sphere by congruent quadrilaterals are completely classified in a series of three papers. This second one applies the powerful tool of trigonometric Diophantine equations to classify the case of 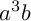$a^3b$-quadrilaterals with all angles being rational degrees. There are 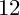$12$ sporadic and 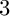$3$ infinite sequences of quadrilaterals admitting the two-layer earth map tilings together with their modifications, and 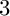$3$ sporadic quadrilaterals admitting $4$ exceptional tilings. Among them only three quadrilaterals are convex. New interesting non-edge-to-edge triangular tilings are obtained as a byproduct.

MSC classification

Primary: 52C20: Tilings in $2$ dimensions 05B45: Tessellation and tiling problems
Type
Article
Information
Nagoya Mathematical Journal , Volume 253 , March 2024 , pp. 128 - 163
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research was supported by key projects of Zhejiang Natural Science Foundation No. LZ22A010003 and ZJNU Shuang-Long Distinguished Professorship Fund No. YS304319159.

References

Akama, Y. and van Cleemput, N., Spherical tilings by congruent quadrangles: Forbidden cases and substructures , Ars Math. Contemp. 8 (2015), 297–318.CrossRefGoogle Scholar
Akama, Y., Wang, E., and Yan, M., Tilings of sphere by congruent pentagons III: Edge combination ${a}^5$ , Adv. Math. 394 (2022), 107881.CrossRefGoogle Scholar
Conway, J. H. and Jones, A. J., Trigonometric diophantine equations (on vanishing sums of roots of unity) , Acta Arithmetica. 30 (1976), 229–240.CrossRefGoogle Scholar
Coolsaet, K., Spherical quadrangles with three equal sides and rational angles , Ars Math. Contemp. 12 (2017), 415–424.CrossRefGoogle Scholar
Dawson, R. J. M. G., Tilings of the sphere with isosceles triangles, Discrete Comput. Geom. 30 (2003), 467–487.CrossRefGoogle Scholar
Dawson, R. J. M. G., An isosceles triangle that tiles the sphere in exactly three ways , Discrete Comput. Geom. 30 (2003), 459–466.CrossRefGoogle Scholar
Dawson, R. J. M. G. and Doyle, B., Tilings of the sphere with right triangles I: The asymptotically right families , Electron. J. Combin. 30 (2006), R48.CrossRefGoogle Scholar
Dawson, R. J. M. G. and Doyle, B., Tilings of the sphere with right triangles II: The(1, 3, 2), (0, 2, n) subfamily , Electron. J. Combin. 13 (2006), R49.CrossRefGoogle Scholar
Dawson, R. J. M. G. and Doyle, B., Tilings of the sphere with right triangles III: The asymptotically obtuse families , Electron. J. Combin. 13 (2007), R48.CrossRefGoogle Scholar
Liao, Y., Qian, P., Wang, E., and Xu, Y., Tilings of the sphere by congruent quadrilaterals I: Edge combination ${a}^2\mathrm{bc}$ , preprint, 2021. arXiv:2110.10087.Google Scholar
Liao, Y., Qian, P., Wang, E., and Xu, Y., Tilings of the sphere by congruent quadrilaterals III: Edge combination ${a}^3b$ with general angles, preprint, 2022. arXiv:2206.15342.Google Scholar
Myerson, G., Rational products of Sines of rational angles , Aequationes Math. 45 (1993), 70–82. https://doi.org/10.1007/bf01844426 CrossRefGoogle Scholar
Sakano, Y. and Akama, Y., Anisohedral spherical triangles and classification of spherical tilings by congruent kites, darts and rhombi , Hiroshima Math. J. 45 (2015), 309–339.CrossRefGoogle Scholar
Ueno, Y. and Agaoka, Y., Examples of spherical tilings by congruent quadrilaterals , Math. Inform. Sci., Fac. Integrated Arts and Sci., Hiroshima Univ., Ser. IV. 27 (2001), 135–144.Google Scholar
Ueno, Y. and Agaoka, Y., Classification of tilings of the 2-dimensional sphere by congruent triangles , Hiroshima Math. J. 32 (2002), 463–540.Google Scholar
Wang, E. and Yan, M., Moduli of pentagonal subdivision tiling, preprint, 2019. arXiv:1907.08776.Google Scholar
Wang, E. and Yan, M., Tilings of the sphere by congruent pentagons I: Edge combinations ${a}^2{b}^2c$ and ${a}^3\mathrm{bc}$ , Adv. Math. 394 (2022), 107866.CrossRefGoogle Scholar
Wang, E. and Yan, M., Tilings of the sphere by congruent pentagons II: Edge combination ${a}^3{b}^2$ , Adv. Math. 394 (2022), 107867.CrossRefGoogle Scholar