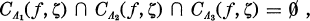Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T15:06:18.140Z Has data issue: false hasContentIssue false
  • English
  • Français

The three-separated-arc property of the modular function

Published online by Cambridge University Press:  22 January 2016

Frederick Bagemihl
Frederick Bagemihl*
Affiliation:
University of Wisconsin-Milwaukee
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D be the open unit disk and Γ be the unit circle in the complex plane, and denote the Riemann sphere by Ω. If f(z) is a function defined on D with values belonging to Ω, if ζ ∈Γ, and if Λ is an arc at ζ then C∈(f, ζ) denotes the cluster set of f at ζ along Λ. If there exist three mutually exclusive arcs Λ1, Λ2, Λ3 at ζ such that

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 61 , July 1976 , pp. 203 - 204
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1976

References

[1] Belna, C.L., Intersections of arc-cluster sets for meromorphic functions, Nagoya Math. J. 40 (1970), 213–220.CrossRefGoogle Scholar