Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
KOIKE, Masao
1986.
Moonshines of <i>PSL</i><sub>2</sub>(<i>F<sub>q</sub></i>) and the automorphism group of Leech lattice.
Japanese journal of mathematics. New series,
Vol. 12,
Issue. 2,
p.
283.
1988.
Vertex Operator Algebras and the Monster.
Vol. 134,
Issue. ,
p.
483.
Koike, Masao
1988.
Modular forms and the automorphism group of Leech lattice.
Nagoya Mathematical Journal,
Vol. 112,
Issue. ,
p.
63.
Harada, Koichiro
and
Lang, Mong Lung
1989.
Some elliptic curves arising from the Leech lattice.
Journal of Algebra,
Vol. 125,
Issue. 2,
p.
298.
Voskresenskaya, G. V.
1992.
Modular forms and group representation.
Mathematical Notes,
Vol. 52,
Issue. 1,
p.
649.
Chan, Shih-Ping
Lang, Mong-Lung
and
Lim, Chong-Hai
1992.
Some modular functions associated to the Lie algebraE 8.
Mathematische Zeitschrift,
Vol. 211,
Issue. 1,
p.
223.
Tuite, Michael P.
1995.
On the relationship between Monstrous Moonshine and the uniqueness of the Moonshine Module.
Communications in Mathematical Physics,
Vol. 166,
Issue. 3,
p.
495.
Kultze, Rolf
1996.
Elliptic genera and the moonshine module.
Mathematische Zeitschrift,
Vol. 223,
Issue. 3,
p.
463.
Kultze, Rolf
1996.
Elliptic genera and the moonshine module.
Mathematische Zeitschrift,
Vol. 223,
Issue. 1,
p.
463.
Rains, E.M
and
Sloane, N.J.A
1998.
The Shadow Theory of Modular and Unimodular Lattices.
Journal of Number Theory,
Vol. 73,
Issue. 2,
p.
359.
Eguchi, Tohru
and
Hikami, Kazuhiro
2012.
Twisted Elliptic Genus for K3 and Borcherds Product.
Letters in Mathematical Physics,
Vol. 102,
Issue. 2,
p.
203.
Cummins, C. J.
and
Duncan, J. F.
2012.
AnE8Correspondence for Multiplicative Eta-Products.
Canadian Mathematical Bulletin,
Vol. 55,
Issue. 1,
p.
67.
Voskresenskaya, G. V.
2014.
The Dedekind Eta-Function in Algebra and Number Theory: Old and New Problems.
Journal of Mathematical Sciences,
Vol. 199,
Issue. 3,
p.
248.
Beneish, Lea
Berg, Jennifer
Goedhart, Eva
Kadhem, Hussain M.
Serrano López, Allechar
and
Treneer, Stephanie
2024.
Replicable functions arising from code-lattice VOAs fixed by automorphisms.
Journal of Algebra,
Vol. 642,
Issue. ,
p.
159.


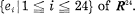 For
For 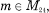 , let
, let