Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T22:55:19.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Theta functions and modular jets

Published online by Cambridge University Press:  22 January 2016

H. D. Fegan
H. D. Fegan*
Affiliation:
Rice University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ⌈ be a subgroup of the modular group PSL(2,Z) then ⌈ acts on the upper half plane H = {zЄC : Im z > 0} and we can form the Riemann surface M = H/⌈, see [3]. The complex line bundles on a Riemann surface M form a group H1(M, 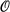*), see [4], and whenever we raise a line bundle to a power it will be in this group. Let κ denote the canonical bundle on M then a modular form of weight ν is a section of the bundle 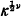. A modular n-jet is then a section of Jn 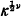the n-th jet bundle, see [7]. We can reformulate these ideas in the following terms. A modular form can be viewed as a function Φ: H → C and a modular n-jet as a vector valued function Φ: H → Cn+1 both of which satisfy a transformation law under the elements of Γ.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 72 , December 1978 , pp. 83 - 92
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1978

References

[1] Fegan, H. D., The heat equation and modularforms, J. Diff. Geom., to appear.Google Scholar
[2] Hermite, Ch., Quelques formules realtives à la transformation des functions elliptiques, J. Math. Pures Appl., 3 (1858), 26’36.Google Scholar
[3] Gunning, R. C., Lectures on modular forms, Princeton University Press, Princeton, 1962.CrossRefGoogle Scholar
[4] Gunning, R. C., Lectures on Riemann surfaces, Princeton University Press, Princeton, 1967.Google Scholar
[5] Kostant, B., On Macdonald’s 97-function formula, the Laplacian and generalzed exponents, Advances in Math., 20 (1976), 179’212.Google Scholar
[6] Kuga, K.andShimura, G., On vector differential forms attached to automorphic forms, Jap. Math. Soc., 12(1960), 258’270.Google Scholar
[7] Palais, R. S., Introduction to global non-linear analysis, Benjamin, New York, 1968. 1968.Google Scholar
[8] Serre, J. P., A course in arithmetic, Springer-Verlag, New York, 1973.Google Scholar