Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alwis, S. P.
and
Kim, Jihn E.
1982.
SupersymmetricSU (11), the invisible axion, and proton decay.
Zeitschrift für Physik C Particles and Fields,
Vol. 13,
Issue. 4,
p.
333.
Schulze-Pillot, R.
1984.
Thetareihen positiv definiter quadratischer Formen.
Inventiones Mathematicae,
Vol. 75,
Issue. 2,
p.
283.
Schulze-Pillot, Rainer
1986.
Ternary quadratic forms and Brandt matrices.
Nagoya Mathematical Journal,
Vol. 102,
Issue. ,
p.
117.
Kramer, J�rg
1986.
Jacobiformen und Thetareihen.
Manuscripta Mathematica,
Vol. 54,
Issue. 3,
p.
279.
Golubeva, E. P.
and
Fomenko, O. M.
1987.
Values of Dirichlet series associated with modular forms at the points S=1/2, 1.
Journal of Soviet Mathematics,
Vol. 36,
Issue. 1,
p.
79.
Kramer, J�rg
1988.
On the linear independence of certain theta-series.
Mathematische Annalen,
Vol. 281,
Issue. 2,
p.
219.
Ponomarev, Paul
1988.
Eichler commutation relations for theta series of nebentypus.
Mathematische Annalen,
Vol. 280,
Issue. 4,
p.
691.
Böcherer, Siegfried
and
Schulze-Pillot, Rainer
1992.
The Dirichlet series of Koecher and Maaß and modular forms of weight 3/2.
Mathematische Zeitschrift,
Vol. 209,
Issue. 1,
p.
273.
Zhuravlev, V. G.
1994.
The correspondence between theta series of ternary and quaternary quadratic forms.
Journal of Mathematical Sciences,
Vol. 70,
Issue. 6,
p.
2097.
Böcherer, Siegfried
and
Schulze‐Pillot, Rainer
1994.
Mellin Transforms of Vector Valued Theta Series Attached to Quaternion Algebras.
Mathematische Nachrichten,
Vol. 169,
Issue. 1,
p.
31.
Lehman, Larry
1997.
Rational eigenvectors in spaces of ternary forms.
Mathematics of Computation,
Vol. 66,
Issue. 218,
p.
833.
Wang, Xueli
and
Pei, Dingyi
2012.
Modular Forms with Integral and Half-Integral Weights.
p.
363.
Guo, Xuejun
Peng, Yuzhen
and
Qin, Hourong
2014.
On the representation numbers of ternary quadratic forms and modular forms of weight 3/2.
Journal of Number Theory,
Vol. 140,
Issue. ,
p.
235.
Lu, Wei
and
Qin, Hourong
2017.
Eichler’s commutation relation and some other invariant subspaces of Hecke operators.
The Ramanujan Journal,
Vol. 44,
Issue. 2,
p.
367.
Voight, John
2023.
Kneser’s method of neighbors.
Archiv der Mathematik,
Vol. 121,
Issue. 5-6,
p.
537.


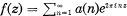 of weight
of weight 