Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T23:30:49.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Surfaces with Mean Curvature Vector Parallel in the Normal Bundle1)

Published online by Cambridge University Press:  22 January 2016

Bang-Yen Chen  and
Gerald D. Ludden
Bang-Yen Chen
Affiliation:
Michigan State University, East Lansing, Mich. 48823
Gerald D. Ludden
Affiliation:
Michigan State University, East Lansing, Mich. 48823
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

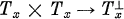Let M be a connected surface immersed in a Euclidean m-space Em. Let h be the second fundamental form of this immersion it is a certain symmetric bilinear mapping for X ∈ M, where Tx is the tangent space and 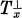the normal space of M at x. Let H be the mean curvature vector of M in Em. If there exists a real λ such that 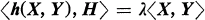for all tangent vectors X, Y in Tx, then ilf is said to be pseudo-umbilical at x.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 47 , September 1972 , pp. 161 - 167
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1972

Footnotes

1)

This paper was presented to the 13th Biennial Seminar of the Canadian Mathematical Congress at Halifax by G. D. Ludden on August 25, 1971.

References

[1] Chen, B.-Y., On the mean curvature of submanifolds of Euclidean space, Bull. Amer. Math. Soc, 77 (1971), 741–743.CrossRefGoogle Scholar
[2] Chen, B.-Y., Pseudo-umbilical submanifolds of a Riemannian manifold of constant curvature, III, J. Differential Geometry (to appear).Google Scholar
[3] Chen, B.-Y., and Ludden, G. D., Rigidity theorems for surfaces in Euclidean space, Bull. Amer. Math. Soc, 78 (1972), 72–73.CrossRefGoogle Scholar
[4] Erbacher, J. A., Isometric immersions with constant mean curvature and triviality of the normal bundle, Nagoya Math. J., 45 (1972), 139–165.CrossRefGoogle Scholar
[5] Itoh, T., Minimal surfaces in 4-dimensional Riemannian manifolds of constant curvature, (to appear).Google Scholar