No CrossRef data available.
Article contents
Sur la Différentiabilité et la Continuité des Potentiels Associés en Valeur Principale À Noyaux Singuliers et M-Fois Régularisant
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
D’après D. Courrège [1], l’opérateur de convolution associé en valeur principale à un noyau de Caldéron-Zygmund homogène de classe C0,μ(∑n) applique continûment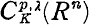 
dans Cp,λ(Rn) si 0 < λ < μ ≤ 1, et l’opérateur de convolution associé à un noyau homogène de degré m—n et de classe Cm,μ(∑n) applique continûment 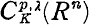dans Cp+m,λ(Rn) si 0 < λ < μ ≤ 1.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1971
References
[1]
Courrège, P.: Noyaux de convolution singuliers opérant sur les fonctions Höldériennes et noyaux de convolution régularisants, Séminaire de probabilités I, Springer-Verlag (1966), 34–51.Google Scholar
[2]
Ito, Y.: Noyaux de convolution en partie finie opérant sur les fonctions Höldériennes, Proc. Jap. Acad., Vol. 45, No. 10 (1969), 907–909.Google Scholar
You have
Access