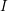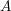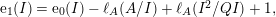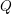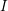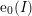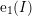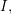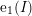1 Introduction and notation
Throughout this paper, let
![]() $A$
denote a Cohen–Macaulay local ring with maximal ideal
$A$
denote a Cohen–Macaulay local ring with maximal ideal
![]() $\mathfrak{m}$
and positive dimension
$\mathfrak{m}$
and positive dimension
![]() $d.$
Let
$d.$
Let
![]() $I$
be an
$I$
be an
![]() $\mathfrak{m}$
-primary ideal in
$\mathfrak{m}$
-primary ideal in
![]() $A$
and, for simplicity, we assume the residue class field
$A$
and, for simplicity, we assume the residue class field
![]() $A/\mathfrak{m}$
is infinite. Let
$A/\mathfrak{m}$
is infinite. Let
![]() $\ell _{A}(N)$
denote, for an
$\ell _{A}(N)$
denote, for an
![]() $A$
-module
$A$
-module
![]() $N$
, the length of
$N$
, the length of
![]() $N$
. The integers
$N$
. The integers
![]() $\{\text{e}_{i}(I)\}_{0\leqslant i\leqslant d}$
such that the equality
$\{\text{e}_{i}(I)\}_{0\leqslant i\leqslant d}$
such that the equality
holds true for all integers
![]() $n\gg 0$
, are called the Hilbert coefficients of
$n\gg 0$
, are called the Hilbert coefficients of
![]() $A$
with respect to
$A$
with respect to
![]() $I$
. This polynomial, known as the Hilbert–Samuel polynomial of
$I$
. This polynomial, known as the Hilbert–Samuel polynomial of
![]() $I$
and denoted by
$I$
and denoted by
![]() $HP_{I}(n),$
encodes the asymptotic information coming from the Hilbert function
$HP_{I}(n),$
encodes the asymptotic information coming from the Hilbert function
![]() $H_{I}(t)$
of
$H_{I}(t)$
of
![]() $I$
which is defined as
$I$
which is defined as
The generating function of the numerical function
![]() $H_{I}(t)$
is the power series
$H_{I}(t)$
is the power series
This series is called the Hilbert series of
![]() $I.$
It is well known that this series is rational and that, even more, there exists a polynomial
$I.$
It is well known that this series is rational and that, even more, there exists a polynomial
![]() $h_{I}(z)$
with integer coefficients such that
$h_{I}(z)$
with integer coefficients such that
![]() $h_{I}(1)\not =0$
and
$h_{I}(1)\not =0$
and
Notice that for all
![]() $i\geqslant 0,$
the Hilbert coefficients can be computed as it follows
$i\geqslant 0,$
the Hilbert coefficients can be computed as it follows
where
![]() $h_{I}^{(i)}(1)$
denotes the
$h_{I}^{(i)}(1)$
denotes the
![]() $i$
th derivative of
$i$
th derivative of
![]() $h_{I}(z)$
evaluated at
$h_{I}(z)$
evaluated at
![]() $1$
(
$1$
(
![]() $h^{(0)}=h_{I}$
).
$h^{(0)}=h_{I}$
).
Choose a parameter ideal
![]() $Q$
of
$Q$
of
![]() $A$
which forms a reduction of
$A$
which forms a reduction of
![]() $I$
and let
$I$
and let
denote, respectively, the Rees algebras of
![]() $I$
and
$I$
and
![]() $Q$
. Let
$Q$
. Let
 $$\begin{eqnarray}\displaystyle & & \displaystyle R^{\prime }=\text{R}^{\prime }(I):=A[It,t^{-1}]\subseteq A[t,t^{-1}]\quad \operatorname{and}\quad \nonumber\\ \displaystyle & & \displaystyle G=\text{G}(I):=R^{\prime }/t^{-1}R^{\prime }\cong \bigoplus _{n\geqslant 0}I^{n}/I^{n+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle R^{\prime }=\text{R}^{\prime }(I):=A[It,t^{-1}]\subseteq A[t,t^{-1}]\quad \operatorname{and}\quad \nonumber\\ \displaystyle & & \displaystyle G=\text{G}(I):=R^{\prime }/t^{-1}R^{\prime }\cong \bigoplus _{n\geqslant 0}I^{n}/I^{n+1}.\nonumber\end{eqnarray}$$
Following Vasconcelos [Reference VasconcelosV], we consider
the Sally module of
![]() $I$
with respect to
$I$
with respect to
![]() $Q$
.
$Q$
.
The notion of filtration of the Sally module was introduced by Vaz Pinto [Reference Vaz PintoVP] as follows. We denote by
![]() $E(\unicode[STIX]{x1D6FC})$
, for a graded
$E(\unicode[STIX]{x1D6FC})$
, for a graded
![]() $T$
-module
$T$
-module
![]() $E$
and each
$E$
and each
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{Z}$
, the graded
$\unicode[STIX]{x1D6FC}\in \mathbb{Z}$
, the graded
![]() $T$
-module whose grading is given by
$T$
-module whose grading is given by
![]() $[E(\unicode[STIX]{x1D6FC})]_{n}=E_{\unicode[STIX]{x1D6FC}+n}$
for all
$[E(\unicode[STIX]{x1D6FC})]_{n}=E_{\unicode[STIX]{x1D6FC}+n}$
for all
![]() $n\in \mathbb{Z}$
.
$n\in \mathbb{Z}$
.
Definition 1.1. [Reference Vaz PintoVP]
We set, for each
![]() $i\geqslant 1$
,
$i\geqslant 1$
,
and let
![]() $L^{(i)}=T[C^{(i)}]_{i}$
. Then, because
$L^{(i)}=T[C^{(i)}]_{i}$
. Then, because
![]() $L^{(i)}\cong \bigoplus _{n\geqslant i}Q^{n-i}I^{i+1}/Q^{n-i+1}I^{i}$
and
$L^{(i)}\cong \bigoplus _{n\geqslant i}Q^{n-i}I^{i+1}/Q^{n-i+1}I^{i}$
and
![]() $C^{(i)}/L^{(i)}\cong C^{(i+1)}$
as graded
$C^{(i)}/L^{(i)}\cong C^{(i+1)}$
as graded
![]() $T$
-modules, we have the following natural exact sequences of graded
$T$
-modules, we have the following natural exact sequences of graded
![]() $T$
-modules
$T$
-modules
for every
![]() $i\geqslant 1.$
$i\geqslant 1.$
We notice that
![]() $C^{(1)}=S$
, and
$C^{(1)}=S$
, and
![]() $C^{(i)}$
are finitely generated graded
$C^{(i)}$
are finitely generated graded
![]() $T$
-modules for all
$T$
-modules for all
![]() $i\geqslant 1$
, since
$i\geqslant 1$
, since
![]() $R$
is a module-finite extension of the graded ring
$R$
is a module-finite extension of the graded ring
![]() $T$
.
$T$
.
So, from now on, we set
and we shall explore the structure of
![]() $C.$
Assume that
$C.$
Assume that
![]() $I$
is integrally closed. Then, by [Reference Elias and VallaEV, Reference Guerrieri and RossiGR], the inequality
$I$
is integrally closed. Then, by [Reference Elias and VallaEV, Reference Guerrieri and RossiGR], the inequality
holds true and the equality
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
holds if and only if
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
holds if and only if
![]() $I^{3}=QI^{2}$
. When this is the case, the associated graded ring
$I^{3}=QI^{2}$
. When this is the case, the associated graded ring
![]() $G$
of
$G$
of
![]() $I$
is Cohen–Macaulay and the behavior of the Hilbert–Samuel function
$I$
is Cohen–Macaulay and the behavior of the Hilbert–Samuel function
![]() $\ell _{A}(A/I^{n+1})$
of
$\ell _{A}(A/I^{n+1})$
of
![]() $I$
is known (see [Reference Elias and VallaEV], Corollary 2.10). Thus the integrally closed ideal
$I$
is known (see [Reference Elias and VallaEV], Corollary 2.10). Thus the integrally closed ideal
![]() $I$
with
$I$
with
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
enjoys nice properties and it seems natural to ask what happens to the integrally closed ideal
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
enjoys nice properties and it seems natural to ask what happens to the integrally closed ideal
![]() $I$
which satisfies the equality
$I$
which satisfies the equality
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. The problem is not trivial even if we consider
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. The problem is not trivial even if we consider
![]() $d=1.$
$d=1.$
We notice here that
![]() $\ell _{A}(I^{2}/QI)=\text{e}_{0}(I)+(d-1)\ell _{A}(A/I)-\ell _{A}(I/I^{2})$
holds true (see for instance [Reference Rossi and VallaRV3]), so that
$\ell _{A}(I^{2}/QI)=\text{e}_{0}(I)+(d-1)\ell _{A}(A/I)-\ell _{A}(I/I^{2})$
holds true (see for instance [Reference Rossi and VallaRV3]), so that
![]() $\ell _{A}(I^{2}/QI)$
does not depend on a minimal reduction
$\ell _{A}(I^{2}/QI)$
does not depend on a minimal reduction
![]() $Q$
of
$Q$
of
![]() $I$
.
$I$
.
Let
![]() $B=T/\mathfrak{m}T\cong (A/\mathfrak{m})[X_{1},X_{2},\ldots ,X_{d}]$
which is a polynomial ring with
$B=T/\mathfrak{m}T\cong (A/\mathfrak{m})[X_{1},X_{2},\ldots ,X_{d}]$
which is a polynomial ring with
![]() $d$
indeterminates over the field
$d$
indeterminates over the field
![]() $A/\mathfrak{m}$
. The main result of this paper is stated as follows.
$A/\mathfrak{m}$
. The main result of this paper is stated as follows.
Theorem 1.2. Assume that
![]() $I$
is integrally closed. Then the following conditions are equivalent:
$I$
is integrally closed. Then the following conditions are equivalent:
-
(1)
 $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
,
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
, -
(2)
 $\mathfrak{m}C=(0)$
and
$\mathfrak{m}C=(0)$
and
 $\text{rank}_{B}C=1$
,
$\text{rank}_{B}C=1$
, -
(3)
 $C\cong (X_{1},X_{2},\ldots ,X_{c})B(-1)$
as graded
$C\cong (X_{1},X_{2},\ldots ,X_{c})B(-1)$
as graded
 $T$
-modules for some
$T$
-modules for some
 $1\leqslant c\leqslant d$
, where
$1\leqslant c\leqslant d$
, where
 $X_{1},X_{2},\ldots ,X_{d}$
are linearly independent linear forms of the polynomial ring
$X_{1},X_{2},\ldots ,X_{d}$
are linearly independent linear forms of the polynomial ring
 $B$
.
$B$
.
When this is the case,
![]() $c=\ell _{A}(I^{3}/QI^{2})$
and
$c=\ell _{A}(I^{3}/QI^{2})$
and
![]() $I^{4}=QI^{3}$
, and the following assertions hold true:
$I^{4}=QI^{3}$
, and the following assertions hold true:
-
(i)
 $\text{depth}~G\geqslant d-c$
and
$\text{depth}~G\geqslant d-c$
and
 $\text{depth}_{T}C=d-c+1$
,
$\text{depth}_{T}C=d-c+1$
, -
(ii)
 $\text{depth}~G=d-c$
, if
$\text{depth}~G=d-c$
, if
 $c\geqslant 2$
.
$c\geqslant 2$
. -
(iii) Suppose
 $c=1<d$
. Then
$c=1<d$
. Then
 $HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
$HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
 $n\geqslant 0$
and
$n\geqslant 0$
and $$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)+1 & \quad \text{if }i=2,\\ 1 & \quad \text{if }i=3\text{ and }d\geqslant 3,\\ 0 & \quad \text{if }4\leqslant i\leqslant d.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)+1 & \quad \text{if }i=2,\\ 1 & \quad \text{if }i=3\text{ and }d\geqslant 3,\\ 0 & \quad \text{if }4\leqslant i\leqslant d.\end{array}\right.\end{eqnarray}$$
-
(iv) Suppose
 $2\leqslant c<d$
. Then
$2\leqslant c<d$
. Then
 $HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
$HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
 $n\geqslant 0$
and
$n\geqslant 0$
and $$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I) & \quad \text{if }i=2,\\ 0 & \quad \text{if }i\neq c+1,c+2,\quad 3\leqslant i\leqslant d\\ (-1)^{c+1} & \quad \text{if }i=c+1,c+2,\quad 3\leqslant i\leqslant d\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I) & \quad \text{if }i=2,\\ 0 & \quad \text{if }i\neq c+1,c+2,\quad 3\leqslant i\leqslant d\\ (-1)^{c+1} & \quad \text{if }i=c+1,c+2,\quad 3\leqslant i\leqslant d\end{array}\right.\end{eqnarray}$$
-
(v) Suppose
 $c=d$
. Then
$c=d$
. Then
 $HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
$HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
 $n\geqslant 2$
and
$n\geqslant 2$
and $$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I) & \quad \text{if }i=2\text{ and }d\geqslant 2,\\ 0 & \quad \text{if }3\leqslant i\leqslant d\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I) & \quad \text{if }i=2\text{ and }d\geqslant 2,\\ 0 & \quad \text{if }3\leqslant i\leqslant d\end{array}\right.\end{eqnarray}$$
-
(vi) The Hilbert series
 $HS_{I}(z)$
is given by
$HS_{I}(z)$
is given by  $$\begin{eqnarray}HS_{I}(z)=\frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-\ell _{A}(I^{2}/QI)-1\}z+\{\ell _{A}(I^{2}/QI)+1\}z^{2}+(1-z)^{c+1}z}{(1-z)^{d}}.\end{eqnarray}$$
$$\begin{eqnarray}HS_{I}(z)=\frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-\ell _{A}(I^{2}/QI)-1\}z+\{\ell _{A}(I^{2}/QI)+1\}z^{2}+(1-z)^{c+1}z}{(1-z)^{d}}.\end{eqnarray}$$
Let us briefly explain how this paper is organized. We shall prove Theorem 1.2 in Section 3. In Section 2 we will introduce some auxiliary results on the structure of the
![]() $T$
-module
$T$
-module
![]() $C=\text{C}_{Q}(I)=(I^{2}R/I^{2}T)(-1)$
, some of them are stated in a general setting. Our hope is that this information will be successfully applied to give new insight to problems related to the structure of the Sally module. In Section 4 we will introduce some consequences of Theorem 1.2. In particular, we shall explore the integrally closed ideals
$C=\text{C}_{Q}(I)=(I^{2}R/I^{2}T)(-1)$
, some of them are stated in a general setting. Our hope is that this information will be successfully applied to give new insight to problems related to the structure of the Sally module. In Section 4 we will introduce some consequences of Theorem 1.2. In particular, we shall explore the integrally closed ideals
![]() $I$
with
$I$
with
![]() $\text{e}_{1}(I)\leqslant \text{e}_{0}(I)-\ell _{A}(A/I)+3.$
In Section 5 we will construct a class of Cohen–Macaulay local rings satisfying condition (1) in Theorem 1.2.
$\text{e}_{1}(I)\leqslant \text{e}_{0}(I)-\ell _{A}(A/I)+3.$
In Section 5 we will construct a class of Cohen–Macaulay local rings satisfying condition (1) in Theorem 1.2.
2 Preliminary steps
The purpose of this section is to summarize some results on the structure of the graded
![]() $T$
-module
$T$
-module
![]() $C=\text{C}_{Q}(I)=(I^{2}R/I^{2}T)(-1)$
, which we need throughout this paper. Remark that in this section
$C=\text{C}_{Q}(I)=(I^{2}R/I^{2}T)(-1)$
, which we need throughout this paper. Remark that in this section
![]() $I$
is an
$I$
is an
![]() $\mathfrak{m}$
-primary ideal not necessarily integrally closed.
$\mathfrak{m}$
-primary ideal not necessarily integrally closed.
Lemma 2.1. The following assertions hold true.
-
(1)
 $\mathfrak{m}^{\ell }C=(0)$
for integers
$\mathfrak{m}^{\ell }C=(0)$
for integers
 $\ell \gg 0$
; hence
$\ell \gg 0$
; hence
 $\dim _{T}C\leqslant d$
.
$\dim _{T}C\leqslant d$
. -
(2) The homogeneous components
 $\{C_{n}\}_{n\in \mathbb{Z}}$
of the graded
$\{C_{n}\}_{n\in \mathbb{Z}}$
of the graded
 $T$
-module
$T$
-module
 $C$
are given by
$C$
are given by  $$\begin{eqnarray}C_{n}\cong \left\{\begin{array}{@{}rl@{}}(0) & \quad \text{if }n\leqslant 1,\\ I^{n+1}/Q^{n-1}I^{2} & \quad \text{if }n\geqslant 2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}C_{n}\cong \left\{\begin{array}{@{}rl@{}}(0) & \quad \text{if }n\leqslant 1,\\ I^{n+1}/Q^{n-1}I^{2} & \quad \text{if }n\geqslant 2.\end{array}\right.\end{eqnarray}$$
-
(3)
 $C=(0)$
if and only if
$C=(0)$
if and only if
 $I^{3}=QI^{2}$
.
$I^{3}=QI^{2}$
. -
(4)
 $\mathfrak{m}C=(0)$
if and only if
$\mathfrak{m}C=(0)$
if and only if
 $\mathfrak{m}I^{n+1}\subseteq Q^{n-1}I^{2}$
for all
$\mathfrak{m}I^{n+1}\subseteq Q^{n-1}I^{2}$
for all
 $n\geqslant 2$
.
$n\geqslant 2$
. -
(5)
 $C=TC_{2}$
if and only if
$C=TC_{2}$
if and only if
 $I^{4}=QI^{3}$
.
$I^{4}=QI^{3}$
.
Proof. (1) Let
![]() $u=t^{-1}$
and
$u=t^{-1}$
and
![]() $T^{\prime }=\text{R}^{\prime }(Q)$
. Notice that we have
$T^{\prime }=\text{R}^{\prime }(Q)$
. Notice that we have
![]() $C=(I^{2}R/I^{2}T)(-1)\cong (I^{2}R^{\prime }/I^{2}T^{\prime })(-1)$
as graded
$C=(I^{2}R/I^{2}T)(-1)\cong (I^{2}R^{\prime }/I^{2}T^{\prime })(-1)$
as graded
![]() $T$
-modules. We then have
$T$
-modules. We then have
![]() $u^{\ell }\cdot (I^{2}R^{\prime }/I^{2}T^{\prime })=(0)$
for some
$u^{\ell }\cdot (I^{2}R^{\prime }/I^{2}T^{\prime })=(0)$
for some
![]() $\ell \gg 0$
, because the graded
$\ell \gg 0$
, because the graded
![]() $T^{\prime }$
-module
$T^{\prime }$
-module
![]() $I^{2}R^{\prime }/I^{2}T^{\prime }$
is finitely generated and
$I^{2}R^{\prime }/I^{2}T^{\prime }$
is finitely generated and
![]() $[I^{2}R^{\prime }/I^{2}T^{\prime }]_{n}=(0)$
for all
$[I^{2}R^{\prime }/I^{2}T^{\prime }]_{n}=(0)$
for all
![]() $n\leqslant 0$
. Therefore,
$n\leqslant 0$
. Therefore,
![]() $\mathfrak{m}^{\ell }C=(0)$
for
$\mathfrak{m}^{\ell }C=(0)$
for
![]() $\ell \gg 0$
, because
$\ell \gg 0$
, because
![]() $Q^{\ell }=(Qt^{\ell })u^{\ell }\subseteq u^{\ell }T^{\prime }\cap A$
and
$Q^{\ell }=(Qt^{\ell })u^{\ell }\subseteq u^{\ell }T^{\prime }\cap A$
and
![]() $\mathfrak{m}=\sqrt{Q}$
.
$\mathfrak{m}=\sqrt{Q}$
.
(2) Since
![]() $[I^{2}R]_{n}=(I^{n+2})t^{n}$
and
$[I^{2}R]_{n}=(I^{n+2})t^{n}$
and
![]() $[I^{2}T]_{n}=(I^{2}Q^{n})t^{n}$
for all
$[I^{2}T]_{n}=(I^{2}Q^{n})t^{n}$
for all
![]() $n\geqslant 0$
, assertion (2) follows from the definition of the module
$n\geqslant 0$
, assertion (2) follows from the definition of the module
![]() $C=(I^{2}R/I^{2}T)(-1)$
.
$C=(I^{2}R/I^{2}T)(-1)$
.
Assertions (3), (4), and (5) readily follow from assertion (2). ◻
In the following result we need that
![]() $Q\cap I^{2}=QI$
holds true. This condition is automatically satisfied in the case where
$Q\cap I^{2}=QI$
holds true. This condition is automatically satisfied in the case where
![]() $I$
is integrally closed (see [Reference HunekeH, Reference ItohI2]).
$I$
is integrally closed (see [Reference HunekeH, Reference ItohI2]).
Proposition 2.2. Suppose that
![]() $Q\cap I^{2}=QI$
. Then we have
$Q\cap I^{2}=QI$
. Then we have
![]() $\text{Ass}_{T}C\subseteq \{\mathfrak{m}T\}$
so that
$\text{Ass}_{T}C\subseteq \{\mathfrak{m}T\}$
so that
![]() $\dim _{T}C=d$
, if
$\dim _{T}C=d$
, if
![]() $C\neq (0)$
.
$C\neq (0)$
.
Let
![]() $Q=(a_{1},\ldots ,a_{d})$
be a minimal reduction of
$Q=(a_{1},\ldots ,a_{d})$
be a minimal reduction of
![]() $I.$
In the proof of Proposition 2.2 we need the following lemmata.
$I.$
In the proof of Proposition 2.2 we need the following lemmata.
Lemma 2.3. Suppose that
![]() $Q\cap I^{2}=QI$
. Then we have the equality
$Q\cap I^{2}=QI$
. Then we have the equality
![]() $(a_{1},a_{2},\ldots ,a_{i})\cap Q^{n+1}I^{2}=(a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
for all
$(a_{1},a_{2},\ldots ,a_{i})\cap Q^{n+1}I^{2}=(a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
for all
![]() $n\geqslant 0$
and
$n\geqslant 0$
and
![]() $1\leqslant i\leqslant d$
. Therefore,
$1\leqslant i\leqslant d$
. Therefore,
![]() $a_{1}t\in T$
is a nonzero divisor on
$a_{1}t\in T$
is a nonzero divisor on
![]() $T/I^{2}T$
.
$T/I^{2}T$
.
Proof. We have only to show that
![]() $(a_{1},a_{2},\ldots ,a_{i})\cap Q^{n+1}I^{2}\subseteq (a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
holds true for all
$(a_{1},a_{2},\ldots ,a_{i})\cap Q^{n+1}I^{2}\subseteq (a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
holds true for all
![]() $n\geqslant 0$
. We proceed by induction on
$n\geqslant 0$
. We proceed by induction on
![]() $n$
and
$n$
and
![]() $i$
. We may assume that
$i$
. We may assume that
![]() $i<d$
and that our assertion holds true for
$i<d$
and that our assertion holds true for
![]() $i+1$
. Suppose
$i+1$
. Suppose
![]() $n=0$
and take
$n=0$
and take
![]() $x\in (a_{1},a_{2},\ldots ,a_{i})\cap QI^{2}$
. Then, by the hypothesis of induction on
$x\in (a_{1},a_{2},\ldots ,a_{i})\cap QI^{2}$
. Then, by the hypothesis of induction on
![]() $i$
, we have
$i$
, we have
Then we write
![]() $x=y+a_{i+1}z$
with
$x=y+a_{i+1}z$
with
![]() $y\in (a_{1},a_{2},\ldots ,a_{i})I^{2}$
and
$y\in (a_{1},a_{2},\ldots ,a_{i})I^{2}$
and
![]() $z\in I^{2}$
. Therefore,
$z\in I^{2}$
. Therefore,
![]() $z\in [(a_{1},a_{2},\ldots ,a_{i}):a_{i+1}]\cap I^{2}=(a_{1},a_{2},\ldots ,a_{i})\cap I^{2}\subseteq (a_{1},a_{2},\ldots ,a_{i})\cap QI$
. Notice that, since
$z\in [(a_{1},a_{2},\ldots ,a_{i}):a_{i+1}]\cap I^{2}=(a_{1},a_{2},\ldots ,a_{i})\cap I^{2}\subseteq (a_{1},a_{2},\ldots ,a_{i})\cap QI$
. Notice that, since
![]() $Q/QI\cong (A/I)^{d}$
,
$Q/QI\cong (A/I)^{d}$
,
![]() $(a_{1},a_{2},\ldots ,a_{i})\cap QI=(a_{1},a_{2},\ldots ,a_{i})I$
holds true. Hence, we get
$(a_{1},a_{2},\ldots ,a_{i})\cap QI=(a_{1},a_{2},\ldots ,a_{i})I$
holds true. Hence, we get
![]() $x=y+a_{i+1}z\in (a_{1},a_{2},\ldots ,a_{i})I^{2}$
. Therefore, we have
$x=y+a_{i+1}z\in (a_{1},a_{2},\ldots ,a_{i})I^{2}$
. Therefore, we have
![]() $(a_{1},a_{2},\ldots ,a_{i})\cap QI^{2}=(a_{1},a_{2},\ldots ,a_{i})I^{2}.$
$(a_{1},a_{2},\ldots ,a_{i})\cap QI^{2}=(a_{1},a_{2},\ldots ,a_{i})I^{2}.$
Assume that
![]() $n\geqslant 1$
and that our assertion holds true for
$n\geqslant 1$
and that our assertion holds true for
![]() $n-1$
. Take
$n-1$
. Take
![]() $x\in (a_{1},a_{2},\ldots ,a_{i})\cap Q^{n+1}I^{2}$
. Then, by the hypothesis of induction on
$x\in (a_{1},a_{2},\ldots ,a_{i})\cap Q^{n+1}I^{2}$
. Then, by the hypothesis of induction on
![]() $i$
, we have
$i$
, we have
Write
![]() $x=y+a_{i+1}z$
with
$x=y+a_{i+1}z$
with
![]() $y\in (a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
and
$y\in (a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
and
![]() $z\in Q^{n}I^{2}$
. By the hypothesis of induction on
$z\in Q^{n}I^{2}$
. By the hypothesis of induction on
![]() $n$
, we have
$n$
, we have
![]() $z\in [(a_{1},a_{2},\ldots ,a_{i}):a_{i+1}]\cap Q^{n}I^{2}=(a_{1},a_{2},\ldots ,a_{i})\cap Q^{n}I^{2}=(a_{1},a_{2},\ldots ,a_{i})Q^{n-1}I^{2}$
. Therefore, we get
$z\in [(a_{1},a_{2},\ldots ,a_{i}):a_{i+1}]\cap Q^{n}I^{2}=(a_{1},a_{2},\ldots ,a_{i})\cap Q^{n}I^{2}=(a_{1},a_{2},\ldots ,a_{i})Q^{n-1}I^{2}$
. Therefore, we get
![]() $x=y+a_{i+1}z\in (a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
. Thus,
$x=y+a_{i+1}z\in (a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
. Thus,
![]() $(a_{1},a_{2},\ldots ,a_{i})\cap Q^{n+1}I^{2}=(a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
as required.◻
$(a_{1},a_{2},\ldots ,a_{i})\cap Q^{n+1}I^{2}=(a_{1},a_{2},\ldots ,a_{i})Q^{n}I^{2}$
as required.◻
Lemma 2.4. Suppose that
![]() $Q\cap I^{2}=QI$
. Then
$Q\cap I^{2}=QI$
. Then
![]() $Q^{n+1}\cap Q^{n}I^{2}=Q^{n+1}I$
for all
$Q^{n+1}\cap Q^{n}I^{2}=Q^{n+1}I$
for all
![]() $n\geqslant 0$
.
$n\geqslant 0$
.
Proof. We have only to show that
![]() $Q^{n+1}\cap Q^{n}I^{2}\subseteq Q^{n+1}I$
for
$Q^{n+1}\cap Q^{n}I^{2}\subseteq Q^{n+1}I$
for
![]() $n\geqslant 0$
. Take
$n\geqslant 0$
. Take
![]() $f\in Q^{n+1}\cap Q^{n}I^{2}$
and write
$f\in Q^{n+1}\cap Q^{n}I^{2}$
and write
![]() $f=\sum _{|\unicode[STIX]{x1D6FC}|=n}x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}$
with
$f=\sum _{|\unicode[STIX]{x1D6FC}|=n}x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}$
with
![]() $x_{\unicode[STIX]{x1D6FC}}\in I^{2}$
, where
$x_{\unicode[STIX]{x1D6FC}}\in I^{2}$
, where
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{d})\in \mathbb{Z}^{d}$
and
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{d})\in \mathbb{Z}^{d}$
and
![]() $|\unicode[STIX]{x1D6FC}|=\sum _{i=1}^{d}\unicode[STIX]{x1D6FC}_{i}$
. Then, we have
$|\unicode[STIX]{x1D6FC}|=\sum _{i=1}^{d}\unicode[STIX]{x1D6FC}_{i}$
. Then, we have
![]() $\overline{ft^{n}}=\sum _{|\unicode[STIX]{x1D6FC}|=n}\overline{x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{n}}=0$
in
$\overline{ft^{n}}=\sum _{|\unicode[STIX]{x1D6FC}|=n}\overline{x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{n}}=0$
in
![]() $\text{G}(Q)=\text{R}^{\prime }(Q)/t^{-1}\text{R}^{\prime }(Q)$
, where
$\text{G}(Q)=\text{R}^{\prime }(Q)/t^{-1}\text{R}^{\prime }(Q)$
, where
![]() $\overline{ft^{n}}$
and
$\overline{ft^{n}}$
and
![]() $\overline{x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{n}}=0$
denote the images of
$\overline{x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{n}}=0$
denote the images of
![]() $ft^{n}$
and
$ft^{n}$
and
![]() $x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{n}$
in
$x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{n}$
in
![]() $\text{G}(Q)$
, respectively. Because
$\text{G}(Q)$
, respectively. Because
![]() $\text{G}(Q)\cong (A/Q)[\overline{a_{1}t},\overline{a_{2}t},\ldots ,\overline{a_{d}t}]$
is the polynomial ring over the ring
$\text{G}(Q)\cong (A/Q)[\overline{a_{1}t},\overline{a_{2}t},\ldots ,\overline{a_{d}t}]$
is the polynomial ring over the ring
![]() $A/Q$
, we have
$A/Q$
, we have
![]() $x_{\unicode[STIX]{x1D6FC}}\in Q\cap I^{2}=QI$
. Thus
$x_{\unicode[STIX]{x1D6FC}}\in Q\cap I^{2}=QI$
. Thus
![]() $f\in Q^{n+1}I$
so that
$f\in Q^{n+1}I$
so that
![]() $Q^{n+1}\cap Q^{n}I^{2}=Q^{n+1}I$
holds true.◻
$Q^{n+1}\cap Q^{n}I^{2}=Q^{n+1}I$
holds true.◻
Lemma 2.5. Suppose that
![]() $Q\cap I^{2}=QI$
. Then the following sequences
$Q\cap I^{2}=QI$
. Then the following sequences
-
(1)
 $0\rightarrow T/IT\overset{a_{1}}{\rightarrow }T/I^{2}T\rightarrow T/[I^{2}T+a_{1}T]\rightarrow 0$
, and
$0\rightarrow T/IT\overset{a_{1}}{\rightarrow }T/I^{2}T\rightarrow T/[I^{2}T+a_{1}T]\rightarrow 0$
, and -
(2)
 $0\rightarrow T/[I^{2}T+QT](-1)\overset{a_{1}t}{\rightarrow }T/[I^{2}T+a_{1}T]\rightarrow T/[I^{2}T+\,a_{1}tT+a_{1}T]\rightarrow \,0$
$0\rightarrow T/[I^{2}T+QT](-1)\overset{a_{1}t}{\rightarrow }T/[I^{2}T+a_{1}T]\rightarrow T/[I^{2}T+\,a_{1}tT+a_{1}T]\rightarrow \,0$
of graded
![]() $T$
-modules are exact.
$T$
-modules are exact.
Proof. (1) Let us consider the homomorphism
of graded
![]() $T$
-modules such that
$T$
-modules such that
![]() $\unicode[STIX]{x1D719}(f)=\overline{a_{1}f}$
for
$\unicode[STIX]{x1D719}(f)=\overline{a_{1}f}$
for
![]() $f\in T$
where
$f\in T$
where
![]() $\overline{a_{1}f}$
denotes the image of
$\overline{a_{1}f}$
denotes the image of
![]() $a_{1}f$
in
$a_{1}f$
in
![]() $T/I^{2}T$
. Because
$T/I^{2}T$
. Because
![]() $\unicode[STIX]{x1D719}(IT)=(0)$
and
$\unicode[STIX]{x1D719}(IT)=(0)$
and
![]() $\text{Coker}\unicode[STIX]{x1D719}=T/[I^{2}T+a_{1}T]$
, we have only to show that
$\text{Coker}\unicode[STIX]{x1D719}=T/[I^{2}T+a_{1}T]$
, we have only to show that
![]() $\ker \unicode[STIX]{x1D719}\subseteq IT$
. Take
$\ker \unicode[STIX]{x1D719}\subseteq IT$
. Take
![]() $f\in [\ker \unicode[STIX]{x1D719}]_{n}$
and write
$f\in [\ker \unicode[STIX]{x1D719}]_{n}$
and write
![]() $f=xt^{n}$
with
$f=xt^{n}$
with
![]() $n\geqslant 0$
and
$n\geqslant 0$
and
![]() $x\in Q^{n}$
. Then we have
$x\in Q^{n}$
. Then we have
![]() $a_{1}f=a_{1}xt^{n}\in I^{2}T$
so that
$a_{1}f=a_{1}xt^{n}\in I^{2}T$
so that
![]() $a_{1}x\in Q^{n}I^{2}\cap Q^{n+1}=Q^{n+1}I$
by Lemma 2.4. Because
$a_{1}x\in Q^{n}I^{2}\cap Q^{n+1}=Q^{n+1}I$
by Lemma 2.4. Because
![]() $a_{1}t\in T$
forms a nonzero divisor on
$a_{1}t\in T$
forms a nonzero divisor on
![]() $T/IT$
(notice that
$T/IT$
(notice that
![]() $T/IT\cong (A/I)[\overline{a_{1}t},\overline{a_{2}t},\ldots ,\overline{a_{d}t}]$
is a polynomial ring over the ring
$T/IT\cong (A/I)[\overline{a_{1}t},\overline{a_{2}t},\ldots ,\overline{a_{d}t}]$
is a polynomial ring over the ring
![]() $A/I$
), we have
$A/I$
), we have
![]() $(a_{1})\cap Q^{n+1}I=a_{1}Q^{n}I$
so that
$(a_{1})\cap Q^{n+1}I=a_{1}Q^{n}I$
so that
![]() $x\in Q^{n}I$
. Therefore,
$x\in Q^{n}I$
. Therefore,
![]() $f\in IT$
, and hence
$f\in IT$
, and hence
![]() $\ker \unicode[STIX]{x1D719}\subseteq IT$
. Thus, we get the first required exact sequence.
$\ker \unicode[STIX]{x1D719}\subseteq IT$
. Thus, we get the first required exact sequence.
(2) Let us consider the homomorphism
of graded
![]() $T$
-modules such that
$T$
-modules such that
![]() $\unicode[STIX]{x1D711}(f)=\overline{a_{1}tf}$
for
$\unicode[STIX]{x1D711}(f)=\overline{a_{1}tf}$
for
![]() $f\in T$
where
$f\in T$
where
![]() $\overline{a_{1}tf}$
denotes the image of
$\overline{a_{1}tf}$
denotes the image of
![]() $a_{1}tf$
in
$a_{1}tf$
in
![]() $T/[I^{2}T+a_{1}T]$
. Because
$T/[I^{2}T+a_{1}T]$
. Because
![]() $\unicode[STIX]{x1D711}(I^{2}T+QT)=(0)$
and
$\unicode[STIX]{x1D711}(I^{2}T+QT)=(0)$
and
![]() $\text{Coker}\unicode[STIX]{x1D719}=T/[I^{2}T+a_{1}tT+a_{1}T]$
, we need to show that
$\text{Coker}\unicode[STIX]{x1D719}=T/[I^{2}T+a_{1}tT+a_{1}T]$
, we need to show that
![]() $[\ker \unicode[STIX]{x1D711}]_{n}\subseteq I^{2}T_{n-1}+QT_{n-1}$
for all
$[\ker \unicode[STIX]{x1D711}]_{n}\subseteq I^{2}T_{n-1}+QT_{n-1}$
for all
![]() $n\geqslant 1$
. Take
$n\geqslant 1$
. Take
![]() $f\in [\ker \unicode[STIX]{x1D711}]_{n}$
and write
$f\in [\ker \unicode[STIX]{x1D711}]_{n}$
and write
![]() $f=xt^{n-1}$
with
$f=xt^{n-1}$
with
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $x\in Q^{n-1}$
. Then we have
$x\in Q^{n-1}$
. Then we have
![]() $a_{1}tf=a_{1}xt^{n}\in I^{2}T+a_{1}T$
so that
$a_{1}tf=a_{1}xt^{n}\in I^{2}T+a_{1}T$
so that
![]() $a_{1}x\in Q^{n}I^{2}+a_{1}Q^{n}$
. Write
$a_{1}x\in Q^{n}I^{2}+a_{1}Q^{n}$
. Write
![]() $a_{1}x=y+a_{1}z$
with
$a_{1}x=y+a_{1}z$
with
![]() $y\in Q^{n}I^{2}$
and
$y\in Q^{n}I^{2}$
and
![]() $z\in Q^{n}$
. Then have
$z\in Q^{n}$
. Then have
by Lemma 2.3. Hence
![]() $x-z\in Q^{n-1}I^{2}$
so that
$x-z\in Q^{n-1}I^{2}$
so that
![]() $x\in Q^{n-1}I^{2}+Q^{n}$
. Therefore,
$x\in Q^{n-1}I^{2}+Q^{n}$
. Therefore,
![]() $f\in I^{2}T_{n-1}+QT_{n-1}$
and hence
$f\in I^{2}T_{n-1}+QT_{n-1}$
and hence
![]() $[\ker \unicode[STIX]{x1D711}]_{n}\subseteq I^{2}T_{n-1}+QT_{n-1}$
. Consequently, we get the second required exact sequence.◻
$[\ker \unicode[STIX]{x1D711}]_{n}\subseteq I^{2}T_{n-1}+QT_{n-1}$
. Consequently, we get the second required exact sequence.◻
The following Lemma 2.6 is the crucial fact in the proof of Proposition 2.2.
Lemma 2.6. Assume that
![]() $Q\cap I^{2}=QI$
. Then we have
$Q\cap I^{2}=QI$
. Then we have
![]() $\text{Ass}_{T}(T/I^{2}T)=\{\mathfrak{m}T\}$
.
$\text{Ass}_{T}(T/I^{2}T)=\{\mathfrak{m}T\}$
.
Proof. Take
![]() $P\in \text{Ass}_{T}(T/I^{2}T)$
; then we have
$P\in \text{Ass}_{T}(T/I^{2}T)$
; then we have
![]() $\mathfrak{m}T\subseteq P$
, because
$\mathfrak{m}T\subseteq P$
, because
![]() $\mathfrak{m}^{\ell }(T/I^{2}T)=(0)$
for
$\mathfrak{m}^{\ell }(T/I^{2}T)=(0)$
for
![]() $\ell \gg 0$
. Assume that
$\ell \gg 0$
. Assume that
![]() $\mathfrak{m}T\subsetneq P$
; then
$\mathfrak{m}T\subsetneq P$
; then
![]() $\text{ht}_{T}P\geqslant 2$
, because
$\text{ht}_{T}P\geqslant 2$
, because
![]() $\mathfrak{m}T$
is a height one prime ideal in
$\mathfrak{m}T$
is a height one prime ideal in
![]() $T$
(notice that
$T$
(notice that
![]() $\dim T=d+1$
). Consider the following exact sequences
$\dim T=d+1$
). Consider the following exact sequences
of
![]() $T_{P}$
-modules, which follow from the exact sequences in Lemma 2.5. Then, since
$T_{P}$
-modules, which follow from the exact sequences in Lemma 2.5. Then, since
![]() $\text{depth}_{T_{P}}T_{P}/IT_{P}>0$
(notice that
$\text{depth}_{T_{P}}T_{P}/IT_{P}>0$
(notice that
![]() $T/IT\cong (A/I)[X_{1},X_{2},\ldots ,X_{d}]$
is the polynomial ring with
$T/IT\cong (A/I)[X_{1},X_{2},\ldots ,X_{d}]$
is the polynomial ring with
![]() $d$
indeterminates over the ring
$d$
indeterminates over the ring
![]() $A/I$
) and
$A/I$
) and
![]() $\text{depth}_{T_{P}}T_{P}/I^{2}T_{P}=0$
, we have
$\text{depth}_{T_{P}}T_{P}/I^{2}T_{P}=0$
, we have
![]() $\text{depth}_{T_{P}}T_{P}/[I^{2}T_{P}+a_{1}T_{P}]=0$
by the exact sequence
$\text{depth}_{T_{P}}T_{P}/[I^{2}T_{P}+a_{1}T_{P}]=0$
by the exact sequence
![]() $(\ast _{1})$
. Notice that
$(\ast _{1})$
. Notice that
![]() $T/[I^{2}T+QT]\cong (A/[I^{2}+Q])[X_{1},X_{2},\ldots ,X_{d}]$
is the polynomial rings with
$T/[I^{2}T+QT]\cong (A/[I^{2}+Q])[X_{1},X_{2},\ldots ,X_{d}]$
is the polynomial rings with
![]() $d$
indeterminates over the ring
$d$
indeterminates over the ring
![]() $A/[I^{2}+Q]$
. Hence,
$A/[I^{2}+Q]$
. Hence,
![]() $\text{depth}_{T_{P}}T_{P}/[I^{2}T_{P}+a_{1}tT_{P}+a_{1}T_{P}]=0$
by the exact sequence
$\text{depth}_{T_{P}}T_{P}/[I^{2}T_{P}+a_{1}tT_{P}+a_{1}T_{P}]=0$
by the exact sequence
![]() $(\ast _{2})$
. Then, because
$(\ast _{2})$
. Then, because
![]() $a_{1}t\in \text{Ann}_{T}(T/[I^{2}T+a_{1}tT+a_{1}T])$
, we have
$a_{1}t\in \text{Ann}_{T}(T/[I^{2}T+a_{1}tT+a_{1}T])$
, we have
![]() $a_{1}t\in P$
. Therefore,
$a_{1}t\in P$
. Therefore,
![]() $\text{depth}_{T_{P}}T_{P}/I^{2}T_{P}>0$
by Lemma 2.3; however, it is impossible. Thus,
$\text{depth}_{T_{P}}T_{P}/I^{2}T_{P}>0$
by Lemma 2.3; however, it is impossible. Thus,
![]() $P=\mathfrak{m}T$
as required.◻
$P=\mathfrak{m}T$
as required.◻
Let us now give a proof of Proposition 2.2.
Proof of Proposition 2.2.
Take
![]() $P\in \text{Ass}_{T}C$
. Then we have
$P\in \text{Ass}_{T}C$
. Then we have
![]() $\mathfrak{m}T\subseteq P$
, because
$\mathfrak{m}T\subseteq P$
, because
![]() $\mathfrak{m}^{\ell }C=(0)$
for some
$\mathfrak{m}^{\ell }C=(0)$
for some
![]() $\ell \gg 0$
by Lemma 2.1(1). Suppose that
$\ell \gg 0$
by Lemma 2.1(1). Suppose that
![]() $\mathfrak{m}T\subsetneq P$
; then
$\mathfrak{m}T\subsetneq P$
; then
![]() $\text{ht}_{T}P\geqslant 2$
, because
$\text{ht}_{T}P\geqslant 2$
, because
![]() $\mathfrak{m}T$
is a height one prime ideal in
$\mathfrak{m}T$
is a height one prime ideal in
![]() $T$
. We look at the following exact sequences
$T$
. We look at the following exact sequences
of
![]() $T_{P}$
-modules which follow from the canonical exact sequences
$T_{P}$
-modules which follow from the canonical exact sequences
of
![]() $T$
-modules. We notice here that
$T$
-modules. We notice here that
![]() $\text{depth}_{T_{P}}I^{2}R_{P}>0$
, because
$\text{depth}_{T_{P}}I^{2}R_{P}>0$
, because
![]() $a_{1}\in A$
is a nonzero divisor on
$a_{1}\in A$
is a nonzero divisor on
![]() $I^{2}R$
. Thanks to the depth lemma and the exact sequence
$I^{2}R$
. Thanks to the depth lemma and the exact sequence
![]() $(\ast _{3})$
, we get
$(\ast _{3})$
, we get
![]() $\text{depth}_{T_{P}}I^{2}T_{P}=1$
, because
$\text{depth}_{T_{P}}I^{2}T_{P}=1$
, because
![]() $\text{depth}_{T_{P}}I^{2}R_{P}>0$
and
$\text{depth}_{T_{P}}I^{2}R_{P}>0$
and
![]() $\text{depth}_{T_{P}}C_{P}=0$
. Then, since
$\text{depth}_{T_{P}}C_{P}=0$
. Then, since
![]() $\text{depth}_{T_{P}}T_{P}\geqslant 2$
, we have
$\text{depth}_{T_{P}}T_{P}\geqslant 2$
, we have
![]() $\text{depth}_{T_{P}}T_{P}/I^{2}T_{P}=0$
by the exact sequence
$\text{depth}_{T_{P}}T_{P}/I^{2}T_{P}=0$
by the exact sequence
![]() $(\ast _{4})$
. Therefore, we have
$(\ast _{4})$
. Therefore, we have
![]() $P=\mathfrak{m}T$
by Lemma 2.6, which is impossible. Thus,
$P=\mathfrak{m}T$
by Lemma 2.6, which is impossible. Thus,
![]() $P=\mathfrak{m}T$
as required.◻
$P=\mathfrak{m}T$
as required.◻
The following techniques are due to Vaz Pinto [Reference Vaz PintoVP, Section 2].
Let
![]() $L=L^{(1)}=TS_{1}$
then
$L=L^{(1)}=TS_{1}$
then
![]() $L\cong \bigoplus _{n\geqslant 1}Q^{n-1}I^{2}/Q^{n}I$
and
$L\cong \bigoplus _{n\geqslant 1}Q^{n-1}I^{2}/Q^{n}I$
and
![]() $S/L\cong C$
as graded
$S/L\cong C$
as graded
![]() $T$
-modules. Then there exists a canonical exact sequence
$T$
-modules. Then there exists a canonical exact sequence
of graded
![]() $T$
-modules (Definition 1.1). We set
$T$
-modules (Definition 1.1). We set
![]() $D=(I^{2}/QI)\otimes _{A}(T/\text{Ann}_{A}(I^{2}/QI)T)$
. Notice here that
$D=(I^{2}/QI)\otimes _{A}(T/\text{Ann}_{A}(I^{2}/QI)T)$
. Notice here that
![]() $D$
forms a graded
$D$
forms a graded
![]() $T$
-module and
$T$
-module and
![]() $T/\text{Ann}_{A}(I^{2}/QI)T\cong (A/\text{Ann}_{A}(I^{2}/QI))[X_{1},X_{2},\ldots ,X_{d}]$
is the polynomial ring with
$T/\text{Ann}_{A}(I^{2}/QI)T\cong (A/\text{Ann}_{A}(I^{2}/QI))[X_{1},X_{2},\ldots ,X_{d}]$
is the polynomial ring with
![]() $d$
indeterminates over the ring
$d$
indeterminates over the ring
![]() $A/\text{Ann}_{A}(I^{2}/QI)$
. Let
$A/\text{Ann}_{A}(I^{2}/QI)$
. Let
denote an epimorphism of graded
![]() $T$
-modules such that
$T$
-modules such that
![]() $\unicode[STIX]{x1D703}(\sum _{\unicode[STIX]{x1D6FC}}\overline{x_{\unicode[STIX]{x1D6FC}}}\otimes X_{1}^{\unicode[STIX]{x1D6FC}_{1}}X_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FC}_{d}})=\sum _{\unicode[STIX]{x1D6FC}}\overline{x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{|\unicode[STIX]{x1D6FC}|+1}}$
for
$\unicode[STIX]{x1D703}(\sum _{\unicode[STIX]{x1D6FC}}\overline{x_{\unicode[STIX]{x1D6FC}}}\otimes X_{1}^{\unicode[STIX]{x1D6FC}_{1}}X_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FC}_{d}})=\sum _{\unicode[STIX]{x1D6FC}}\overline{x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{|\unicode[STIX]{x1D6FC}|+1}}$
for
![]() $x_{\unicode[STIX]{x1D6FC}}\in I^{2}$
and
$x_{\unicode[STIX]{x1D6FC}}\in I^{2}$
and
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{d})\in \mathbb{Z}^{d}$
with
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{d})\in \mathbb{Z}^{d}$
with
![]() $\unicode[STIX]{x1D6FC}_{i}\geqslant 0$
$\unicode[STIX]{x1D6FC}_{i}\geqslant 0$
![]() $(1\leqslant i\leqslant d)$
, where
$(1\leqslant i\leqslant d)$
, where
![]() $|\unicode[STIX]{x1D6FC}|=\sum _{i=1}^{d}\unicode[STIX]{x1D6FC}_{i}$
, and
$|\unicode[STIX]{x1D6FC}|=\sum _{i=1}^{d}\unicode[STIX]{x1D6FC}_{i}$
, and
![]() $\overline{x_{\unicode[STIX]{x1D6FC}}}$
and
$\overline{x_{\unicode[STIX]{x1D6FC}}}$
and
![]() $\overline{x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{|\unicode[STIX]{x1D6FC}|+1}}$
denote the images of
$\overline{x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{|\unicode[STIX]{x1D6FC}|+1}}$
denote the images of
![]() $x_{\unicode[STIX]{x1D6FC}}$
in
$x_{\unicode[STIX]{x1D6FC}}$
in
![]() $I^{2}/QI$
and
$I^{2}/QI$
and
![]() $x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{|\unicode[STIX]{x1D6FC}|+1}$
in
$x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FC}_{d}}t^{|\unicode[STIX]{x1D6FC}|+1}$
in
![]() $L$
.
$L$
.
Then we have the following lemma.
Lemma 2.7. Suppose that
![]() $Q\cap I^{2}=QI$
. Then the map
$Q\cap I^{2}=QI$
. Then the map
![]() $\unicode[STIX]{x1D703}:D(-1)\rightarrow L$
is an isomorphism of graded
$\unicode[STIX]{x1D703}:D(-1)\rightarrow L$
is an isomorphism of graded
![]() $T$
-modules.
$T$
-modules.
Proof. We have only to show that
![]() $\ker \unicode[STIX]{x1D703}=(0)$
. Assume that
$\ker \unicode[STIX]{x1D703}=(0)$
. Assume that
![]() $\ker \unicode[STIX]{x1D703}\neq (0)$
and let
$\ker \unicode[STIX]{x1D703}\neq (0)$
and let
![]() $n\geqslant 2$
as the least integer so that
$n\geqslant 2$
as the least integer so that
![]() $[\ker \unicode[STIX]{x1D703}]_{n}\neq (0)$
(notice that
$[\ker \unicode[STIX]{x1D703}]_{n}\neq (0)$
(notice that
![]() $[\ker \unicode[STIX]{x1D703}]_{n}=(0)$
for all
$[\ker \unicode[STIX]{x1D703}]_{n}=(0)$
for all
![]() $n\leqslant 1$
). Take
$n\leqslant 1$
). Take
![]() $0\neq g\in [\ker \unicode[STIX]{x1D703}]_{n}$
and we set
$0\neq g\in [\ker \unicode[STIX]{x1D703}]_{n}$
and we set
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4} & = & \displaystyle \left\{(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{d-1},0)\in \mathbb{Z}^{d}|\unicode[STIX]{x1D6FC}_{i}\geqslant 0\text{ for }1\leqslant i\leqslant d-1,\text{ and }\mathop{\sum }_{i=1}^{d-1}\unicode[STIX]{x1D6FC}_{i}=n-1\right\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6E4}^{\prime } & = & \displaystyle \left\{(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\ldots ,\unicode[STIX]{x1D6FD}_{d})\in \mathbb{Z}^{d}|\unicode[STIX]{x1D6FD}_{i}\geqslant 0\text{ for }1\leqslant i\leqslant d-1,\unicode[STIX]{x1D6FD}_{d}\geqslant 1,\text{ and }\!\mathop{\sum }_{i=1}^{d}\unicode[STIX]{x1D6FD}_{i}=n-1\right\}\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4} & = & \displaystyle \left\{(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{d-1},0)\in \mathbb{Z}^{d}|\unicode[STIX]{x1D6FC}_{i}\geqslant 0\text{ for }1\leqslant i\leqslant d-1,\text{ and }\mathop{\sum }_{i=1}^{d-1}\unicode[STIX]{x1D6FC}_{i}=n-1\right\},\nonumber\\ \displaystyle \unicode[STIX]{x1D6E4}^{\prime } & = & \displaystyle \left\{(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\ldots ,\unicode[STIX]{x1D6FD}_{d})\in \mathbb{Z}^{d}|\unicode[STIX]{x1D6FD}_{i}\geqslant 0\text{ for }1\leqslant i\leqslant d-1,\unicode[STIX]{x1D6FD}_{d}\geqslant 1,\text{ and }\!\mathop{\sum }_{i=1}^{d}\unicode[STIX]{x1D6FD}_{i}=n-1\right\}\!.\nonumber\end{eqnarray}$$
Then because
we may write
 $$\begin{eqnarray}\displaystyle g & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}\cup \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FC}}}\otimes X_{1}^{\unicode[STIX]{x1D6FC}_{1}}X_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FC}_{d}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}}\overline{x_{\unicode[STIX]{x1D6FC}}}\otimes X_{1}^{\unicode[STIX]{x1D6FC}_{1}}X_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots X_{d-1}^{\unicode[STIX]{x1D6FC}_{d-1}}+\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}\cup \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FC}}}\otimes X_{1}^{\unicode[STIX]{x1D6FC}_{1}}X_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FC}_{d}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}}\overline{x_{\unicode[STIX]{x1D6FC}}}\otimes X_{1}^{\unicode[STIX]{x1D6FC}_{1}}X_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots X_{d-1}^{\unicode[STIX]{x1D6FC}_{d-1}}+\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}},\nonumber\end{eqnarray}$$
where
![]() $\overline{x_{\unicode[STIX]{x1D6FC}}},\overline{x_{\unicode[STIX]{x1D6FD}}}$
denote the images of
$\overline{x_{\unicode[STIX]{x1D6FC}}},\overline{x_{\unicode[STIX]{x1D6FD}}}$
denote the images of
![]() $x_{\unicode[STIX]{x1D6FC}},x_{\unicode[STIX]{x1D6FD}}\in I^{2}$
in
$x_{\unicode[STIX]{x1D6FC}},x_{\unicode[STIX]{x1D6FD}}\in I^{2}$
in
![]() $I^{2}/QI$
, respectively. We may assume that
$I^{2}/QI$
, respectively. We may assume that
![]() $\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}}\neq 0$
in
$\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}}\neq 0$
in
![]() $D$
. Then we have
$D$
. Then we have
so that
Because
![]() $Q^{n}I=(a_{1},a_{2},\ldots ,a_{d-1})^{n}I+a_{d}Q^{n-1}I$
and
$Q^{n}I=(a_{1},a_{2},\ldots ,a_{d-1})^{n}I+a_{d}Q^{n-1}I$
and
![]() $\unicode[STIX]{x1D6FD}_{d}\geqslant 1$
, we may write
$\unicode[STIX]{x1D6FD}_{d}\geqslant 1$
, we may write
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}}x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d-1}^{\unicode[STIX]{x1D6FC}_{d-1}}+a_{d}\left(\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}x_{\unicode[STIX]{x1D6FD}}a_{1}^{\unicode[STIX]{x1D6FD}_{1}}a_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FD}_{d}-1}\right)=\unicode[STIX]{x1D70F}+a_{d}\unicode[STIX]{x1D70C}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}}x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d-1}^{\unicode[STIX]{x1D6FC}_{d-1}}+a_{d}\left(\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}x_{\unicode[STIX]{x1D6FD}}a_{1}^{\unicode[STIX]{x1D6FD}_{1}}a_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FD}_{d}-1}\right)=\unicode[STIX]{x1D70F}+a_{d}\unicode[STIX]{x1D70C}\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D70F}\in (a_{1},a_{2},\ldots ,a_{d-1})^{n}I$
and
$\unicode[STIX]{x1D70F}\in (a_{1},a_{2},\ldots ,a_{d-1})^{n}I$
and
![]() $\unicode[STIX]{x1D70C}\in Q^{n-1}I$
. Then because
$\unicode[STIX]{x1D70C}\in Q^{n-1}I$
. Then because
 $$\begin{eqnarray}\displaystyle a_{d}\left(\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}x_{\unicode[STIX]{x1D6FD}}a_{1}^{\unicode[STIX]{x1D6FD}_{1}}a_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FD}_{d}-1}-\unicode[STIX]{x1D70C}\right) & = & \displaystyle \unicode[STIX]{x1D70F}-\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}}x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d-1}^{\unicode[STIX]{x1D6FC}_{d-1}}\nonumber\\ \displaystyle & & \displaystyle \in (a_{1},a_{2},\ldots ,a_{d-1})^{n-1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{d}\left(\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}x_{\unicode[STIX]{x1D6FD}}a_{1}^{\unicode[STIX]{x1D6FD}_{1}}a_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FD}_{d}-1}-\unicode[STIX]{x1D70C}\right) & = & \displaystyle \unicode[STIX]{x1D70F}-\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}}x_{\unicode[STIX]{x1D6FC}}a_{1}^{\unicode[STIX]{x1D6FC}_{1}}a_{2}^{\unicode[STIX]{x1D6FC}_{2}}\cdots a_{d-1}^{\unicode[STIX]{x1D6FC}_{d-1}}\nonumber\\ \displaystyle & & \displaystyle \in (a_{1},a_{2},\ldots ,a_{d-1})^{n-1}\nonumber\end{eqnarray}$$
we have, by Lemma 2.4,
Therefore,
![]() $\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}x_{\unicode[STIX]{x1D6FD}}a_{1}^{\unicode[STIX]{x1D6FD}_{1}}a_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FD}_{d}-1}\in Q^{n-1}I$
and hence
$\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}x_{\unicode[STIX]{x1D6FD}}a_{1}^{\unicode[STIX]{x1D6FD}_{1}}a_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots a_{d}^{\unicode[STIX]{x1D6FD}_{d}-1}\in Q^{n-1}I$
and hence
![]() $\unicode[STIX]{x1D703}(\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}-1})=0$
. Then, because
$\unicode[STIX]{x1D703}(\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}-1})=0$
. Then, because
![]() $\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}-1}\in [\ker \unicode[STIX]{x1D703}]_{n-1}=(0)$
, we have
$\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}-1}\in [\ker \unicode[STIX]{x1D703}]_{n-1}=(0)$
, we have
![]() $\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}}=0$
, which is contradiction. Thus
$\sum _{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}^{\prime }}\overline{x_{\unicode[STIX]{x1D6FD}}}\otimes X_{1}^{\unicode[STIX]{x1D6FD}_{1}}X_{2}^{\unicode[STIX]{x1D6FD}_{2}}\cdots X_{d}^{\unicode[STIX]{x1D6FD}_{d}}=0$
, which is contradiction. Thus
![]() $\ker \unicode[STIX]{x1D703}=(0)$
. Consequently, the map
$\ker \unicode[STIX]{x1D703}=(0)$
. Consequently, the map
![]() $\unicode[STIX]{x1D703}:D(-1)\rightarrow L$
is an isomorphism.◻
$\unicode[STIX]{x1D703}:D(-1)\rightarrow L$
is an isomorphism.◻
Thanks to Lemma 2.7, we can prove the following result.
Proposition 2.8. Suppose that
![]() $Q\cap I^{2}=QI$
. Then we have
$Q\cap I^{2}=QI$
. Then we have
 $$\begin{eqnarray}\displaystyle \ell _{A}(A/I^{n+1}) & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}\!-\{\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)\}\binom{n+d-1}{d-1}\nonumber\\ \displaystyle & & \displaystyle +\,\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}-\ell _{A}(C_{n})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{A}(A/I^{n+1}) & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}\!-\{\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)\}\binom{n+d-1}{d-1}\nonumber\\ \displaystyle & & \displaystyle +\,\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}-\ell _{A}(C_{n})\nonumber\end{eqnarray}$$
for all
![]() $n\geqslant 0$
.
$n\geqslant 0$
.
Proof. We have, for all
![]() $n\geqslant 0$
,
$n\geqslant 0$
,
 $$\begin{eqnarray}\displaystyle \ell _{A}(S_{n}) & = & \displaystyle \ell _{A}(L_{n})+\ell _{A}(C_{n})\nonumber\\ \displaystyle & = & \displaystyle \ell _{A}(I^{2}/QI)\binom{n+d-2}{d-1}+\ell _{A}(C_{n})\nonumber\\ \displaystyle & = & \displaystyle \ell _{A}(I^{2}/QI)\binom{n+d-1}{d-1}-\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}+\ell _{A}(C_{n})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{A}(S_{n}) & = & \displaystyle \ell _{A}(L_{n})+\ell _{A}(C_{n})\nonumber\\ \displaystyle & = & \displaystyle \ell _{A}(I^{2}/QI)\binom{n+d-2}{d-1}+\ell _{A}(C_{n})\nonumber\\ \displaystyle & = & \displaystyle \ell _{A}(I^{2}/QI)\binom{n+d-1}{d-1}-\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}+\ell _{A}(C_{n})\nonumber\end{eqnarray}$$
by the exact sequence
and the isomorphisms
![]() $L\cong D(-1)\cong (I^{2}/QI)\otimes _{A}(A/\text{Ann}_{A}(I^{2}/QI))[X_{1},X_{2},\ldots ,X_{d}]$
of graded
$L\cong D(-1)\cong (I^{2}/QI)\otimes _{A}(A/\text{Ann}_{A}(I^{2}/QI))[X_{1},X_{2},\ldots ,X_{d}]$
of graded
![]() $T$
-modules (see Lemma 2.7). Therefore, we have, for all
$T$
-modules (see Lemma 2.7). Therefore, we have, for all
![]() $n\geqslant 0$
,
$n\geqslant 0$
,
 $$\begin{eqnarray}\displaystyle \ell _{A}(A/I^{n+1}) & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)\}\binom{n+d-1}{d-1}-\ell _{A}(S_{n})\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)\}\binom{n+d-1}{d-1}-\!\{\!\ell _{A}(I^{2}/QI)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\binom{n+d-1}{d-1}-\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}+\ell _{A}(C_{n})\!\}\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)\}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\binom{n+d-1}{d-1}+\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}-\ell _{A}(C_{n})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{A}(A/I^{n+1}) & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)\}\binom{n+d-1}{d-1}-\ell _{A}(S_{n})\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)\}\binom{n+d-1}{d-1}-\!\{\!\ell _{A}(I^{2}/QI)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\binom{n+d-1}{d-1}-\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}+\ell _{A}(C_{n})\!\}\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)\}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\binom{n+d-1}{d-1}+\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}-\ell _{A}(C_{n})\nonumber\end{eqnarray}$$
by [Reference Goto, Nishida and OzekiGNO, Proposition 2.2 (2)]. ◻
The following result specifies [Reference Goto, Nishida and OzekiGNO, Proposition 2.2(3)] and, by using Propositions 2.2 and 2.8, the proof takes advantage of the same techniques.
Proposition 2.9. Suppose that
![]() $Q\cap I^{2}=QI$
. Let
$Q\cap I^{2}=QI$
. Let
![]() $\mathfrak{p}=\mathfrak{m}T$
. Then we have
$\mathfrak{p}=\mathfrak{m}T$
. Then we have
Combining Lemma 2.1(3) and Proposition 2.9 we obtain the following result that was proven by Elias and Valla [Reference Elias and VallaEV, Theorem 2.1] in the case where
![]() $I=\mathfrak{m}$
.
$I=\mathfrak{m}$
.
Corollary 2.10. Suppose that
![]() $Q\cap I^{2}=QI$
. Then we have
$Q\cap I^{2}=QI$
. Then we have
![]() $\text{e}_{1}(I)\geqslant \text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
. The equality
$\text{e}_{1}(I)\geqslant \text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
. The equality
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
holds true if and only if
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
holds true if and only if
![]() $I^{3}=QI^{2}$
. When this is the case,
$I^{3}=QI^{2}$
. When this is the case,
![]() $\text{e}_{2}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)$
if
$\text{e}_{2}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)$
if
![]() $d\geqslant 2$
,
$d\geqslant 2$
,
![]() $\text{e}_{i}(I)=0$
for all
$\text{e}_{i}(I)=0$
for all
![]() $3\leqslant i\leqslant d$
, and
$3\leqslant i\leqslant d$
, and
![]() $G$
is a Cohen–Macaulay ring.
$G$
is a Cohen–Macaulay ring.
Let us introduce the relationship between the depth of the module
![]() $C$
and the associated graded ring
$C$
and the associated graded ring
![]() $G$
of
$G$
of
![]() $I$
.
$I$
.
Lemma 2.11. Suppose that
![]() $Q\cap I^{2}=QI$
and
$Q\cap I^{2}=QI$
and
![]() $C\neq (0)$
. Let
$C\neq (0)$
. Let
![]() $s=\text{depth}_{T}C$
. Then we have
$s=\text{depth}_{T}C$
. Then we have
![]() $\text{depth}G\geqslant s-1$
. In particular, we have
$\text{depth}G\geqslant s-1$
. In particular, we have
![]() $\text{depth}G=s-1$
, if
$\text{depth}G=s-1$
, if
![]() $s\leqslant d-2$
.
$s\leqslant d-2$
.
Proof. Notice that
![]() $L\cong D(-1)$
by Lemma 2.7 and
$L\cong D(-1)$
by Lemma 2.7 and
![]() $D$
is a
$D$
is a
![]() $d$
dimensional Cohen–Macaulay
$d$
dimensional Cohen–Macaulay
![]() $T$
-module. Therefore, we have
$T$
-module. Therefore, we have
![]() $s\leqslant \text{depth}_{T}S$
and, if
$s\leqslant \text{depth}_{T}S$
and, if
![]() $s\leqslant d-2$
then
$s\leqslant d-2$
then
![]() $s=\text{depth}_{T}S$
by the exact sequence
$s=\text{depth}_{T}S$
by the exact sequence
Because
![]() $\text{depth}G\geqslant \text{depth}_{T}S-1$
and, if
$\text{depth}G\geqslant \text{depth}_{T}S-1$
and, if
![]() $\text{depth}_{T}S\leqslant d-1$
then
$\text{depth}_{T}S\leqslant d-1$
then
![]() $\text{depth}G=\text{depth}_{T}S-1$
by [Reference Goto, Nishida and OzekiGNO, Proposition 2.2(4)], our assertions follow.◻
$\text{depth}G=\text{depth}_{T}S-1$
by [Reference Goto, Nishida and OzekiGNO, Proposition 2.2(4)], our assertions follow.◻
3 Proof of Theorem 1.2
The purpose of this section is to prove Theorem 1.2. Throughout this section, let
![]() $I$
be an integrally closed
$I$
be an integrally closed
![]() $\mathfrak{m}$
-primary ideal.
$\mathfrak{m}$
-primary ideal.
Theorem 3.1. Suppose that
![]() $I$
is integrally closed. Then the following conditions are equivalent:
$I$
is integrally closed. Then the following conditions are equivalent:
-
(1)
 $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
,
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
, -
(2)
 $\mathfrak{m}C=(0)$
and
$\mathfrak{m}C=(0)$
and
 $\text{rank}_{B}C=1$
,
$\text{rank}_{B}C=1$
, -
(3) there exists a non-zero graded ideal
 $\mathfrak{a}$
of
$\mathfrak{a}$
of
 $B$
such that
$B$
such that
 $C\cong \mathfrak{a}(-1)$
as graded
$C\cong \mathfrak{a}(-1)$
as graded
 $T$
-modules.
$T$
-modules.
To prove Theorem 3.1, we need the following bound on
![]() $\text{e}_{2}(I)$
.
$\text{e}_{2}(I)$
.
Lemma 3.2. ([Reference ItohI1, Theorem 12], [Reference SallyS2, Corollary 2.5], [Reference Rossi and VallaRV3, Corollary 3.1])
Suppose
![]() $d\geqslant 2$
and let
$d\geqslant 2$
and let
![]() $I$
be an integrally closed ideal. Then
$I$
be an integrally closed ideal. Then
![]() $\text{e}_{2}(I)\geqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I).$
$\text{e}_{2}(I)\geqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I).$
Proof of Theorem 3.1.
Let
![]() $\mathfrak{p}=\mathfrak{m}T$
; then we see that
$\mathfrak{p}=\mathfrak{m}T$
; then we see that
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+\ell _{T_{\mathfrak{p}}}(C_{\mathfrak{p}})$
by Lemma 2.9 and
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+\ell _{T_{\mathfrak{p}}}(C_{\mathfrak{p}})$
by Lemma 2.9 and
![]() $\text{Ass}_{T}C=\{\mathfrak{p}\}$
byProposition 2.2.
$\text{Ass}_{T}C=\{\mathfrak{p}\}$
byProposition 2.2.
![]() $(1)\Rightarrow (2)$
Since
$(1)\Rightarrow (2)$
Since
![]() $\ell _{T_{\mathfrak{p}}}(C_{\mathfrak{p}})=1$
and
$\ell _{T_{\mathfrak{p}}}(C_{\mathfrak{p}})=1$
and
![]() $\text{Ass}_{T}C=\{\mathfrak{p}\}$
, we have
$\text{Ass}_{T}C=\{\mathfrak{p}\}$
, we have
![]() $\mathfrak{m}C=(0)$
and
$\mathfrak{m}C=(0)$
and
![]() $\text{rank}_{B}C=1$
.
$\text{rank}_{B}C=1$
.
![]() $(2)\Rightarrow (1)$
This is clear, because assertion
$(2)\Rightarrow (1)$
This is clear, because assertion
![]() $(1)$
is equivalent to saying that
$(1)$
is equivalent to saying that
![]() $\ell _{T_{\mathfrak{p}}}(C_{\mathfrak{p}})=1$
.
$\ell _{T_{\mathfrak{p}}}(C_{\mathfrak{p}})=1$
.
![]() $(3)\Rightarrow (2)$
This is obvious.
$(3)\Rightarrow (2)$
This is obvious.
![]() $(2)\Rightarrow (3)$
Because
$(2)\Rightarrow (3)$
Because
![]() $\text{Ass}_{T}C=\{\mathfrak{p}\}$
,
$\text{Ass}_{T}C=\{\mathfrak{p}\}$
,
![]() $C$
is a torsion free
$C$
is a torsion free
![]() $B$
-module. If
$B$
-module. If
![]() $C$
is
$C$
is
![]() $B$
-free, then we have
$B$
-free, then we have
![]() $C\cong B(-2)$
as graded
$C\cong B(-2)$
as graded
![]() $B$
-modules, because
$B$
-modules, because
![]() $C_{2}\neq (0)$
and
$C_{2}\neq (0)$
and
![]() $C_{n}=(0)$
for
$C_{n}=(0)$
for
![]() $n\leqslant 1$
. Hence
$n\leqslant 1$
. Hence
![]() $C\cong X_{1}B(-1)$
as graded
$C\cong X_{1}B(-1)$
as graded
![]() $B$
-modules with
$B$
-modules with
![]() $0\neq X_{1}\in B_{1}$
.
$0\neq X_{1}\in B_{1}$
.
Suppose that
![]() $C$
is not
$C$
is not
![]() $B$
-free. Then we have
$B$
-free. Then we have
![]() $d=\dim A\geqslant 2$
. Because
$d=\dim A\geqslant 2$
. Because
![]() $\text{rank}_{B}C=1$
, there exists a graded ideal
$\text{rank}_{B}C=1$
, there exists a graded ideal
![]() $\mathfrak{a}$
of
$\mathfrak{a}$
of
![]() $B$
such that
$B$
such that
as graded
![]() $B$
-modules for some
$B$
-modules for some
![]() $r\in \mathbb{Z}$
. Since every height one prime in the polynomial ring
$r\in \mathbb{Z}$
. Since every height one prime in the polynomial ring
![]() $B$
is principal, we may choose
$B$
is principal, we may choose
![]() $\mathfrak{a}$
with
$\mathfrak{a}$
with
![]() $\text{ht}_{B}\mathfrak{a}\geqslant 2$
. Then since
$\text{ht}_{B}\mathfrak{a}\geqslant 2$
. Then since
![]() $\mathfrak{a}_{r+2}\cong \mathfrak{a}(r)_{2}\cong C_{2}\neq (0)$
and
$\mathfrak{a}_{r+2}\cong \mathfrak{a}(r)_{2}\cong C_{2}\neq (0)$
and
![]() $\mathfrak{a}_{n}=(0)$
for all
$\mathfrak{a}_{n}=(0)$
for all
![]() $n\leqslant 0$
, we have
$n\leqslant 0$
, we have
![]() $r+2\geqslant 1$
so that
$r+2\geqslant 1$
so that
![]() $r\geqslant -1$
. It is now enough to show that
$r\geqslant -1$
. It is now enough to show that
![]() $r=-1$
. Applying the exact sequence
$r=-1$
. Applying the exact sequence
of graded
![]() $B$
-modules, we have
$B$
-modules, we have
 $$\begin{eqnarray}\displaystyle \ell _{A}(C_{n}) & = & \displaystyle \ell _{A}(B_{r+n})-\ell _{A}([B/\mathfrak{a}]_{r+n})\nonumber\\ \displaystyle & = & \displaystyle \binom{n+r+d-1}{d-1}-\ell _{A}([B/\mathfrak{a}]_{r+n})\nonumber\\ \displaystyle & = & \displaystyle \binom{n+d-1}{d-1}+r\binom{n+d-2}{d-2}+\text{(lower terms)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{A}(C_{n}) & = & \displaystyle \ell _{A}(B_{r+n})-\ell _{A}([B/\mathfrak{a}]_{r+n})\nonumber\\ \displaystyle & = & \displaystyle \binom{n+r+d-1}{d-1}-\ell _{A}([B/\mathfrak{a}]_{r+n})\nonumber\\ \displaystyle & = & \displaystyle \binom{n+d-1}{d-1}+r\binom{n+d-2}{d-2}+\text{(lower terms)}\nonumber\end{eqnarray}$$
for all
![]() $n\gg 0$
, because
$n\gg 0$
, because
![]() $\text{ht}_{B}\mathfrak{a}\geqslant 2$
. Therefore, thanks to Proposition 2.8, we have
$\text{ht}_{B}\mathfrak{a}\geqslant 2$
. Therefore, thanks to Proposition 2.8, we have
 $$\begin{eqnarray}\displaystyle \ell _{A}(A/I^{n+1}) & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)\}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\binom{n+d-1}{d-1}+\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}-\ell _{A}(C_{n})\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1\}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\binom{n+d-1}{d-1}+\{\ell _{A}(I^{2}/QI)\,-r\}\binom{n+d-2}{d-2}+\text{(lower terms)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{A}(A/I^{n+1}) & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)\}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\binom{n+d-1}{d-1}+\ell _{A}(I^{2}/QI)\binom{n+d-2}{d-2}-\ell _{A}(C_{n})\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}(I)\binom{n+d}{d}-\{\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1\}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\binom{n+d-1}{d-1}+\{\ell _{A}(I^{2}/QI)\,-r\}\binom{n+d-2}{d-2}+\text{(lower terms)}\nonumber\end{eqnarray}$$
for all
![]() $n\gg 0$
. Therefore,
$n\gg 0$
. Therefore,
![]() $\text{e}_{2}(I)=\ell _{A}(I^{2}/QI)-r$
. Then, because
$\text{e}_{2}(I)=\ell _{A}(I^{2}/QI)-r$
. Then, because
![]() $\text{e}_{2}(I)\geqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)=\ell _{A}(I^{2}/QI)+1$
by Lemma 3.2 we have
$\text{e}_{2}(I)\geqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)=\ell _{A}(I^{2}/QI)+1$
by Lemma 3.2 we have
![]() $r\leqslant -1$
. Thus
$r\leqslant -1$
. Thus
![]() $r=-1$
and so
$r=-1$
and so
![]() $C\cong \mathfrak{a}(-1)$
as graded
$C\cong \mathfrak{a}(-1)$
as graded
![]() $B$
-modules.◻
$B$
-modules.◻
As a direct consequence of Theorem 3.1 the following result holds true.
Proposition 3.3. Assume that
![]() $I$
is integrally closed. Suppose that
$I$
is integrally closed. Suppose that
![]() $\text{e}_{1}(I)\,=\,\text{e}_{0}(I)\,-\,\ell _{A}(\!A/I)\,+\,\ell _{A}(I^{2}/QI)\,+\,1\!$
and
$\text{e}_{1}(I)\,=\,\text{e}_{0}(I)\,-\,\ell _{A}(\!A/I)\,+\,\ell _{A}(I^{2}/QI)\,+\,1\!$
and
![]() $I^{4}\,=\,QI^{3}$
. Let
$I^{4}\,=\,QI^{3}$
. Let
![]() $c\,=\,\ell _{A}(I^{3}/QI^{2})$
. Then
$c\,=\,\ell _{A}(I^{3}/QI^{2})$
. Then
-
(1)
 $1\leqslant c\leqslant d$
and
$1\leqslant c\leqslant d$
and
 $\unicode[STIX]{x1D707}_{B}(C)=c$
.
$\unicode[STIX]{x1D707}_{B}(C)=c$
. -
(2)
 $\text{depth}~G\geqslant d-c$
and
$\text{depth}~G\geqslant d-c$
and
 $\text{depth}_{T}C=d-c+1$
,
$\text{depth}_{T}C=d-c+1$
, -
(3)
 $\text{depth}~G=d-c$
, if
$\text{depth}~G=d-c$
, if
 $c\geqslant 2$
.
$c\geqslant 2$
. -
(4) Suppose
 $c=1<d$
. Then
$c=1<d$
. Then
 $HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
$HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
 $n\geqslant 0$
and
$n\geqslant 0$
and  $$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)+1 & \quad \text{if }i=2,\\ 1 & \quad \text{if }i=3\text{ and }d\geqslant 3,\\ 0 & \quad \text{if }4\leqslant i\leqslant d.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)+1 & \quad \text{if }i=2,\\ 1 & \quad \text{if }i=3\text{ and }d\geqslant 3,\\ 0 & \quad \text{if }4\leqslant i\leqslant d.\end{array}\right.\end{eqnarray}$$
-
(5) Suppose
 $2\leqslant c<d$
. Then
$2\leqslant c<d$
. Then
 $HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
$HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
 $n\geqslant 0$
and
$n\geqslant 0$
and  $$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I) & \quad \text{if }i=2,\\ 0 & \quad \text{if }i\neq c+1,c+2,3\leqslant i\leqslant d,\\ (-1)^{c+1} & \quad \text{if }i=c+1,c+2,3\leqslant i\leqslant d,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I) & \quad \text{if }i=2,\\ 0 & \quad \text{if }i\neq c+1,c+2,3\leqslant i\leqslant d,\\ (-1)^{c+1} & \quad \text{if }i=c+1,c+2,3\leqslant i\leqslant d,\end{array}\right.\end{eqnarray}$$
-
(6) Suppose
 $c=d$
. Then
$c=d$
. Then
 $HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
$HP_{I}(n)=\ell _{A}(A/I^{n+1})$
for all
 $n\geqslant 2$
and
$n\geqslant 2$
and  $$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I) & \quad \text{if }i=2\text{ and }d\geqslant 2,\\ 0 & \quad \text{if }3\leqslant i\leqslant d,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\text{e}_{i}(I)=\left\{\begin{array}{@{}ll@{}}\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I) & \quad \text{if }i=2\text{ and }d\geqslant 2,\\ 0 & \quad \text{if }3\leqslant i\leqslant d,\end{array}\right.\end{eqnarray}$$
-
(7) The Hilbert series
 $HS_{I}(z)$
is given by
$HS_{I}(z)$
is given by  $$\begin{eqnarray}HS_{I}(z)=\frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-\ell _{A}(I^{2}/QI)-1\}z+\{\ell _{A}(I^{2}/QI)+1\}z^{2}+(1-z)^{c+1}z}{(1-z)^{d}}.\end{eqnarray}$$
$$\begin{eqnarray}HS_{I}(z)=\frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-\ell _{A}(I^{2}/QI)-1\}z+\{\ell _{A}(I^{2}/QI)+1\}z^{2}+(1-z)^{c+1}z}{(1-z)^{d}}.\end{eqnarray}$$
Proof.
![]() $(1)$
We have
$(1)$
We have
![]() $C=TC_{2}$
, since
$C=TC_{2}$
, since
![]() $I^{4}=QI^{3}$
(cf. Lemma 2.1(5)). Therefore, thanks to Theorem 3.1,
$I^{4}=QI^{3}$
(cf. Lemma 2.1(5)). Therefore, thanks to Theorem 3.1,
![]() $C\cong \mathfrak{a}(-1)$
as graded
$C\cong \mathfrak{a}(-1)$
as graded
![]() $T$
-modules, where
$T$
-modules, where
![]() $\mathfrak{a}=(X_{1},X_{2},\ldots ,X_{c})B$
is an ideal generated by linear forms
$\mathfrak{a}=(X_{1},X_{2},\ldots ,X_{c})B$
is an ideal generated by linear forms
![]() $\{X_{i}\}_{1\leqslant i\leqslant c}$
of
$\{X_{i}\}_{1\leqslant i\leqslant c}$
of
![]() $B$
. Hence, we get
$B$
. Hence, we get
![]() $1\leqslant c\leqslant d$
and
$1\leqslant c\leqslant d$
and
![]() $\unicode[STIX]{x1D707}_{B}(C)=c$
.
$\unicode[STIX]{x1D707}_{B}(C)=c$
.
![]() $(4)$
,
$(4)$
,
![]() $(5)$
,
$(5)$
,
![]() $(6)$
Let us consider the exact sequence
$(6)$
Let us consider the exact sequence
of graded
![]() $B$
-modules. Then, we have
$B$
-modules. Then, we have
 $$\begin{eqnarray}\displaystyle \ell _{A}(C_{n}) & = & \displaystyle \ell _{A}(B_{n-1})-\ell _{A}([B/\mathfrak{a}]_{n-1})\nonumber\\ \displaystyle & = & \displaystyle \binom{n-1+d-1}{d-1}-\binom{n-1+d-c-1}{d-c-1}\nonumber\\ \displaystyle & = & \displaystyle \binom{n+d-1}{d-1}-\binom{n+d-2}{d-2}-\binom{n+d-c-1}{d-c-1}\nonumber\\ \displaystyle & & \displaystyle +\,\binom{n+d-c-2}{d-c-2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{A}(C_{n}) & = & \displaystyle \ell _{A}(B_{n-1})-\ell _{A}([B/\mathfrak{a}]_{n-1})\nonumber\\ \displaystyle & = & \displaystyle \binom{n-1+d-1}{d-1}-\binom{n-1+d-c-1}{d-c-1}\nonumber\\ \displaystyle & = & \displaystyle \binom{n+d-1}{d-1}-\binom{n+d-2}{d-2}-\binom{n+d-c-1}{d-c-1}\nonumber\\ \displaystyle & & \displaystyle +\,\binom{n+d-c-2}{d-c-2}\nonumber\end{eqnarray}$$
for all
![]() $n\geqslant 0$
(resp.
$n\geqslant 0$
(resp.
![]() $n\geqslant 2$
) if
$n\geqslant 2$
) if
![]() $1\leqslant c\leqslant d-1$
(resp.
$1\leqslant c\leqslant d-1$
(resp.
![]() $c=d$
). Therefore, our assertions
$c=d$
). Therefore, our assertions
![]() $(4)$
,
$(4)$
,
![]() $(5)$
, and
$(5)$
, and
![]() $(6)$
follow by Proposition 2.8.
$(6)$
follow by Proposition 2.8.
(7) We have
by the above exact sequence
![]() $(\ast _{5})$
, where
$(\ast _{5})$
, where
![]() $HS_{\ast }(z)$
denotes the Hilbert series of the graded modules. We also have
$HS_{\ast }(z)$
denotes the Hilbert series of the graded modules. We also have
by the exact sequence
and the isomorphism
![]() $L\cong D(-1)$
of graded
$L\cong D(-1)$
of graded
![]() $T$
-modules (Lemma 2.7). Then, because
$T$
-modules (Lemma 2.7). Then, because
([Reference Vaz PintoVP], [Reference Rossi and VallaRV3, Proposition 6.3]), we can get the required result.
We prove now
![]() $(2)$
,
$(2)$
,
![]() $(3).$
We have
$(3).$
We have
![]() $\text{depth}_{T}C=d-c+1$
by the exact sequence
$\text{depth}_{T}C=d-c+1$
by the exact sequence
![]() $(\ast _{5})$
so that
$(\ast _{5})$
so that
![]() $\text{depth}G\geqslant d-c$
and, if
$\text{depth}G\geqslant d-c$
and, if
![]() $c\geqslant 3,$
then
$c\geqslant 3,$
then
![]() $\text{depth}G=d-c$
by Lemma 2.11. Let us consider the case where
$\text{depth}G=d-c$
by Lemma 2.11. Let us consider the case where
![]() $c=2$
and we need to show
$c=2$
and we need to show
![]() $\text{depth}G=d-2$
. Assume
$\text{depth}G=d-2$
. Assume
![]() $\text{depth}G\geqslant d-1$
; then
$\text{depth}G\geqslant d-1$
; then
![]() $S$
is a Cohen–Macaulay
$S$
is a Cohen–Macaulay
![]() $T$
-module by [Reference Goto, Nishida and OzekiGNO, Proposition 2.2]. Taking the local cohomology functors
$T$
-module by [Reference Goto, Nishida and OzekiGNO, Proposition 2.2]. Taking the local cohomology functors
![]() $\text{H}_{M}^{i}(\ast )$
of
$\text{H}_{M}^{i}(\ast )$
of
![]() $T$
with respect to the graded maximal ideal
$T$
with respect to the graded maximal ideal
![]() $M=\mathfrak{m}T+T_{+}$
to the above exact sequence
$M=\mathfrak{m}T+T_{+}$
to the above exact sequence
![]() $(\dagger )$
of graded
$(\dagger )$
of graded
![]() $T$
-modules, we get a monomorphism
$T$
-modules, we get a monomorphism
of graded
![]() $T$
-modules. Because
$T$
-modules. Because
![]() $C\cong (X_{1},X_{2})B(-1)$
, we have
$C\cong (X_{1},X_{2})B(-1)$
, we have
![]() $\text{H}_{M}^{d-1}(C)\cong \text{H}_{M}^{d-2}(B/(X_{1},X_{2})B)(-1)$
as graded
$\text{H}_{M}^{d-1}(C)\cong \text{H}_{M}^{d-2}(B/(X_{1},X_{2})B)(-1)$
as graded
![]() $T$
-modules so that
$T$
-modules so that
![]() $[\text{H}_{M}^{d-1}(C)]_{-d+3}\neq (0)$
(notice that
$[\text{H}_{M}^{d-1}(C)]_{-d+3}\neq (0)$
(notice that
![]() $B/(X_{1},X_{2})B\cong (A/\mathfrak{m})[X_{3},X_{4},\ldots ,X_{d}]$
). On the other hand, we have
$B/(X_{1},X_{2})B\cong (A/\mathfrak{m})[X_{3},X_{4},\ldots ,X_{d}]$
). On the other hand, we have
![]() $[\text{H}_{M}^{d}(L)]_{n}=(0)$
for all
$[\text{H}_{M}^{d}(L)]_{n}=(0)$
for all
![]() $n\geqslant -d+2$
, because
$n\geqslant -d+2$
, because
![]() $L\cong D(-1)\cong (I^{2}/QI)\otimes _{A}(A/\text{Ann}_{A}(I^{2}/QI))[X_{1},X_{2},\ldots ,X_{d}](-1)$
by Lemma 2.7. However, this is impossible. Therefore,
$L\cong D(-1)\cong (I^{2}/QI)\otimes _{A}(A/\text{Ann}_{A}(I^{2}/QI))[X_{1},X_{2},\ldots ,X_{d}](-1)$
by Lemma 2.7. However, this is impossible. Therefore,
![]() $\text{depth}~G=d-2$
if
$\text{depth}~G=d-2$
if
![]() $c=2$
.◻
$c=2$
.◻
We prove now Theorem 1.2. Assume assertion
![]() $(1)$
in Theorem 1.2. Then we have an isomorphism
$(1)$
in Theorem 1.2. Then we have an isomorphism
![]() $C\cong \mathfrak{a}(-1)$
as graded
$C\cong \mathfrak{a}(-1)$
as graded
![]() $B$
-modules for a graded ideal
$B$
-modules for a graded ideal
![]() $\mathfrak{a}$
in
$\mathfrak{a}$
in
![]() $B$
by Theorem 3.1. Once we are able to show
$B$
by Theorem 3.1. Once we are able to show
![]() $I^{4}=QI^{3}$
, then, because
$I^{4}=QI^{3}$
, then, because
![]() $C=TC_{2}$
by Lemma 2.1(5), the ideal
$C=TC_{2}$
by Lemma 2.1(5), the ideal
![]() $\mathfrak{a}$
is generated by linearly independent linear forms
$\mathfrak{a}$
is generated by linearly independent linear forms
![]() $\{X_{i}\}_{1\leqslant i\leqslant c}$
of
$\{X_{i}\}_{1\leqslant i\leqslant c}$
of
![]() $B$
with
$B$
with
![]() $c=\ell _{A}(I^{3}/QI^{2})$
(recall that
$c=\ell _{A}(I^{3}/QI^{2})$
(recall that
![]() $\mathfrak{a}_{1}\cong C_{2}\cong I^{3}/QI^{2}$
by Lemma 2.1
$\mathfrak{a}_{1}\cong C_{2}\cong I^{3}/QI^{2}$
by Lemma 2.1
![]() $(2)$
). Therefore, the implication
$(2)$
). Therefore, the implication
![]() $(1)\Rightarrow (3)$
in Theorem 1.2 follows. We also notice that, the last assertions of Theorem 1.2 follow by Proposition 3.3.
$(1)\Rightarrow (3)$
in Theorem 1.2 follows. We also notice that, the last assertions of Theorem 1.2 follow by Proposition 3.3.
Thus our Theorem 1.2 has been proven modulo the following theorem.
Theorem 3.4. Assume that
![]() $I$
is integrally closed. Suppose that
$I$
is integrally closed. Suppose that
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. Then
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. Then
![]() $I^{4}=QI^{3}$
.
$I^{4}=QI^{3}$
.
Proof. We proceed by induction on
![]() $d$
. Suppose that
$d$
. Suppose that
![]() $d=1$
. Then the result follows by [Reference Huckaba and MarleyHM, Proposition 4.6] since
$d=1$
. Then the result follows by [Reference Huckaba and MarleyHM, Proposition 4.6] since
![]() $\text{e}_{1}(I)=\sum _{i\geqslant 0}\ell _{A}(I^{i+1}/QI^{i}).$
$\text{e}_{1}(I)=\sum _{i\geqslant 0}\ell _{A}(I^{i+1}/QI^{i}).$
Assume that
![]() $d\geqslant 2$
and that our assertion holds true for
$d\geqslant 2$
and that our assertion holds true for
![]() $d-1$
. Since the residue class field
$d-1$
. Since the residue class field
![]() $A/\mathfrak{m}$
of
$A/\mathfrak{m}$
of
![]() $A$
is infinite, without loss of generality, we may assume that
$A$
is infinite, without loss of generality, we may assume that
![]() $a_{1}$
is a superficial element of
$a_{1}$
is a superficial element of
![]() $I$
and
$I$
and
![]() $I/(a_{1})$
is integrally closed (cf. [Reference ItohI1, p. 648], [Reference Rossi and VallaRV3, Proposition 1.1]). We set
$I/(a_{1})$
is integrally closed (cf. [Reference ItohI1, p. 648], [Reference Rossi and VallaRV3, Proposition 1.1]). We set
![]() $A^{\prime }=A/(a_{1}),I^{\prime }=I/(a_{1}),Q^{\prime }=Q/(a_{1})$
. We then have
$A^{\prime }=A/(a_{1}),I^{\prime }=I/(a_{1}),Q^{\prime }=Q/(a_{1})$
. We then have
![]() $\text{e}_{1}(I^{\prime })=\text{e}_{0}(I^{\prime })-\ell _{A^{\prime }}(A^{\prime }/I^{\prime })+\ell _{A^{\prime }}({I^{\prime }}^{2}/Q^{\prime }I^{\prime })+1$
because
$\text{e}_{1}(I^{\prime })=\text{e}_{0}(I^{\prime })-\ell _{A^{\prime }}(A^{\prime }/I^{\prime })+\ell _{A^{\prime }}({I^{\prime }}^{2}/Q^{\prime }I^{\prime })+1$
because
![]() $\text{e}_{i}(I^{\prime })=\text{e}_{i}(I)$
for
$\text{e}_{i}(I^{\prime })=\text{e}_{i}(I)$
for
![]() $0\leqslant i\leqslant d-1$
,
$0\leqslant i\leqslant d-1$
,
![]() $\ell _{A^{\prime }}(A^{\prime }/I^{\prime })=\ell _{A}(A/I)$
, and since
$\ell _{A^{\prime }}(A^{\prime }/I^{\prime })=\ell _{A}(A/I)$
, and since
![]() $(a_{1})\cap I^{2}=a_{1}I$
,
$(a_{1})\cap I^{2}=a_{1}I$
,
![]() $\ell _{A^{\prime }}({I^{\prime }}^{2}/Q^{\prime }I^{\prime })=\ell _{A}(I^{2}/QI)$
. Then the inductive assumption on
$\ell _{A^{\prime }}({I^{\prime }}^{2}/Q^{\prime }I^{\prime })=\ell _{A}(I^{2}/QI)$
. Then the inductive assumption on
![]() $d$
says that
$d$
says that
![]() ${I^{\prime }}^{4}=Q^{\prime }{I^{\prime }}^{3}$
holds true. If
${I^{\prime }}^{4}=Q^{\prime }{I^{\prime }}^{3}$
holds true. If
![]() $\text{depth}\text{G}(I^{\prime })>0$
then, thanks to Sally’s technique (cf. [Reference SallyS1], [Reference Huckaba and MarleyHM, Lemma 2.2]),
$\text{depth}\text{G}(I^{\prime })>0$
then, thanks to Sally’s technique (cf. [Reference SallyS1], [Reference Huckaba and MarleyHM, Lemma 2.2]),
![]() $a_{1}t$
is a non-zero divisor on
$a_{1}t$
is a non-zero divisor on
![]() $G$
. Then we have
$G$
. Then we have
![]() $I^{4}=QI^{3}$
.
$I^{4}=QI^{3}$
.
Assume that
![]() $\text{depth}\text{G}(I^{\prime })=0$
. Then because
$\text{depth}\text{G}(I^{\prime })=0$
. Then because
![]() $\text{e}_{1}(I^{\prime })=\text{e}_{0}(I^{\prime })-\ell _{A^{\prime }}(A^{\prime }/I^{\prime })+\ell _{A^{\prime }}({I^{\prime }}^{2}/Q^{\prime }I^{\prime })+1$
and
$\text{e}_{1}(I^{\prime })=\text{e}_{0}(I^{\prime })-\ell _{A^{\prime }}(A^{\prime }/I^{\prime })+\ell _{A^{\prime }}({I^{\prime }}^{2}/Q^{\prime }I^{\prime })+1$
and
![]() ${I^{\prime }}^{4}=Q^{\prime }{I^{\prime }}^{3}$
, we have
${I^{\prime }}^{4}=Q^{\prime }{I^{\prime }}^{3}$
, we have
![]() $\ell _{A^{\prime }}({I^{\prime }}^{3}/Q^{\prime }{I^{\prime }}^{2})=d-1$
by Proposition 3.3(2). Since
$\ell _{A^{\prime }}({I^{\prime }}^{3}/Q^{\prime }{I^{\prime }}^{2})=d-1$
by Proposition 3.3(2). Since
![]() ${I^{\prime }}^{3}/Q^{\prime }{I^{\prime }}^{2}$
is a homomorphic image of
${I^{\prime }}^{3}/Q^{\prime }{I^{\prime }}^{2}$
is a homomorphic image of
![]() $I^{3}/QI^{2}$
, we have
$I^{3}/QI^{2}$
, we have
![]() $\ell _{A}(C_{2})=\ell _{A}(I^{3}/QI^{2})\geqslant d-1$
. Let us now take an isomorphism
$\ell _{A}(C_{2})=\ell _{A}(I^{3}/QI^{2})\geqslant d-1$
. Let us now take an isomorphism
of graded
![]() $B$
-modules, where
$B$
-modules, where
![]() $\mathfrak{a}$
is a graded ideal of
$\mathfrak{a}$
is a graded ideal of
![]() $B$
(cf. Theorem 3.1). Then since
$B$
(cf. Theorem 3.1). Then since
![]() $\ell _{A}(\mathfrak{a}_{1})=\ell _{A}(C_{2})\geqslant d-1$
, we have
$\ell _{A}(\mathfrak{a}_{1})=\ell _{A}(C_{2})\geqslant d-1$
, we have
![]() $Y_{1},Y_{2},\ldots ,Y_{d-1}\in \mathfrak{a}$
where
$Y_{1},Y_{2},\ldots ,Y_{d-1}\in \mathfrak{a}$
where
![]() $Y_{1},Y_{2},\ldots ,Y_{d-1}$
denote linearly independent linear forms of
$Y_{1},Y_{2},\ldots ,Y_{d-1}$
denote linearly independent linear forms of
![]() $B$
, which we enlarge to a basis
$B$
, which we enlarge to a basis
![]() $Y_{1},Y_{2},\ldots ,Y_{d-1},Y_{d}$
of
$Y_{1},Y_{2},\ldots ,Y_{d-1},Y_{d}$
of
![]() $B_{1}$
. If
$B_{1}$
. If
![]() $\mathfrak{a}=(Y_{1},Y_{2},\ldots ,Y_{d-1})B$
then, because
$\mathfrak{a}=(Y_{1},Y_{2},\ldots ,Y_{d-1})B$
then, because
![]() $C=TC_{2}$
, we have
$C=TC_{2}$
, we have
![]() $I^{4}=QI^{3}$
by Lemma 2.1(5). Assume that
$I^{4}=QI^{3}$
by Lemma 2.1(5). Assume that
![]() $\mathfrak{a}\neq (Y_{1},Y_{2},\ldots ,Y_{d-1})B$
. Then, since
$\mathfrak{a}\neq (Y_{1},Y_{2},\ldots ,Y_{d-1})B$
. Then, since
![]() $B=k[Y_{1},Y_{2},\ldots ,Y_{d}]$
, the ideal
$B=k[Y_{1},Y_{2},\ldots ,Y_{d}]$
, the ideal
![]() $\mathfrak{a}/(Y_{1},Y_{2},\ldots ,Y_{d-1})$
is principal so that
$\mathfrak{a}/(Y_{1},Y_{2},\ldots ,Y_{d-1})$
is principal so that
![]() $\mathfrak{a}=(Y_{1},Y_{2},\ldots ,Y_{d-1},Y_{d}^{\ell })B$
for some
$\mathfrak{a}=(Y_{1},Y_{2},\ldots ,Y_{d-1},Y_{d}^{\ell })B$
for some
![]() $\ell \geqslant 1$
.
$\ell \geqslant 1$
.
We need the following.
Claim 1. We have
![]() $\ell =1$
or
$\ell =1$
or
![]() $\ell =2$
.
$\ell =2$
.
Proof of Claim 1.
Assume that
![]() $\ell \geqslant 3$
. Then
$\ell \geqslant 3$
. Then
![]() $I^{4}/[QI^{3}+\mathfrak{m}I^{4}]\cong [C/MC]_{3}=(0)$
, where
$I^{4}/[QI^{3}+\mathfrak{m}I^{4}]\cong [C/MC]_{3}=(0)$
, where
![]() $M=\mathfrak{m}T+T_{+}$
denotes the graded maximal ideal of
$M=\mathfrak{m}T+T_{+}$
denotes the graded maximal ideal of
![]() $T$
. Therefore,
$T$
. Therefore,
![]() $I^{4}=QI^{3}$
by Nakayama’s lemma so that
$I^{4}=QI^{3}$
by Nakayama’s lemma so that
![]() $C=TC_{2}$
, which is impossible. Thus
$C=TC_{2}$
, which is impossible. Thus
![]() $\ell =1$
or
$\ell =1$
or
![]() $\ell =2$
.◻
$\ell =2$
.◻
We have to show that
![]() $\ell =1$
. Assume that
$\ell =1$
. Assume that
![]() $\ell =2$
. Let us write, for each
$\ell =2$
. Let us write, for each
![]() $1\leqslant i\leqslant d$
,
$1\leqslant i\leqslant d$
,
![]() $Y_{i}=\overline{b_{i}t}$
with
$Y_{i}=\overline{b_{i}t}$
with
![]() $b_{i}\in Q$
, where
$b_{i}\in Q$
, where
![]() $\overline{b_{i}t}$
denotes the image of
$\overline{b_{i}t}$
denotes the image of
![]() $b_{i}t\in T$
in
$b_{i}t\in T$
in
![]() $B$
. We notice here that
$B$
. We notice here that
![]() $Q=(b_{1},b_{2},\ldots ,b_{d})$
, because
$Q=(b_{1},b_{2},\ldots ,b_{d})$
, because
![]() $Y_{1},Y_{2},\ldots ,Y_{d}$
forms a
$Y_{1},Y_{2},\ldots ,Y_{d}$
forms a
![]() $k$
-basis of
$k$
-basis of
![]() $B_{1}$
.
$B_{1}$
.
Let us choose elements
![]() $f_{i}\in C_{2}$
for
$f_{i}\in C_{2}$
for
![]() $1\leqslant i\leqslant d-1$
and
$1\leqslant i\leqslant d-1$
and
![]() $f_{d}\in C_{3}$
so that
$f_{d}\in C_{3}$
so that
![]() $\unicode[STIX]{x1D711}(f_{i})=Y_{i}$
for
$\unicode[STIX]{x1D711}(f_{i})=Y_{i}$
for
![]() $1\leqslant i\leqslant d-1$
and
$1\leqslant i\leqslant d-1$
and
![]() $\unicode[STIX]{x1D711}(f_{d})=Y_{d}^{2}$
. Let
$\unicode[STIX]{x1D711}(f_{d})=Y_{d}^{2}$
. Let
![]() $z_{i}\in I^{3}$
for
$z_{i}\in I^{3}$
for
![]() $1\leqslant i\leqslant d-1$
and
$1\leqslant i\leqslant d-1$
and
![]() $z_{d}\in I^{4}$
so that
$z_{d}\in I^{4}$
so that
![]() $\{f_{i}\}_{1\leqslant i\leqslant d-1}$
and
$\{f_{i}\}_{1\leqslant i\leqslant d-1}$
and
![]() $f_{d}$
are, respectively, the images of
$f_{d}$
are, respectively, the images of
![]() $\{z_{i}t^{2}\}_{1\leqslant i\leqslant d-1}$
and
$\{z_{i}t^{2}\}_{1\leqslant i\leqslant d-1}$
and
![]() $z_{d}t^{3}$
in
$z_{d}t^{3}$
in
![]() $C$
. Let us now consider the relations
$C$
. Let us now consider the relations
![]() $Y_{d}^{2}f_{i}=Y_{i}f_{d}$
in
$Y_{d}^{2}f_{i}=Y_{i}f_{d}$
in
![]() $C$
for
$C$
for
![]() $1\leqslant i\leqslant d-1$
, that is
$1\leqslant i\leqslant d-1$
, that is
for
![]() $1\leqslant i\leqslant d-1$
. Notice that
$1\leqslant i\leqslant d-1$
. Notice that
by Lemma 2.3 and write
with
![]() $\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{d}\in Q^{2}I^{2}$
. Then we have
$\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{d}\in Q^{2}I^{2}$
. Then we have
so that
![]() $b_{d}z_{1}-\unicode[STIX]{x1D70F}_{d}\in (b_{1})$
because
$b_{d}z_{1}-\unicode[STIX]{x1D70F}_{d}\in (b_{1})$
because
![]() $b_{1},b_{d}$
forms a regular sequence on
$b_{1},b_{d}$
forms a regular sequence on
![]() $A$
. Since
$A$
. Since
![]() $\unicode[STIX]{x1D70F}_{d}\in (b_{1},b_{d})\cap Q^{2}I^{2}=(b_{1},b_{d})QI^{2}$
by Lemma 2.3, there exist elements
$\unicode[STIX]{x1D70F}_{d}\in (b_{1},b_{d})\cap Q^{2}I^{2}=(b_{1},b_{d})QI^{2}$
by Lemma 2.3, there exist elements
![]() $\unicode[STIX]{x1D70F}_{1}^{\prime },\unicode[STIX]{x1D70F}_{d}^{\prime }\in QI^{2}$
such that
$\unicode[STIX]{x1D70F}_{1}^{\prime },\unicode[STIX]{x1D70F}_{d}^{\prime }\in QI^{2}$
such that
![]() $\unicode[STIX]{x1D70F}_{d}=b_{1}\unicode[STIX]{x1D70F}_{1}^{\prime }+b_{d}\unicode[STIX]{x1D70F}_{d}^{\prime }$
. Then by the equality
$\unicode[STIX]{x1D70F}_{d}=b_{1}\unicode[STIX]{x1D70F}_{1}^{\prime }+b_{d}\unicode[STIX]{x1D70F}_{d}^{\prime }$
. Then by the equality
![]() $(1)$
we have
$(1)$
we have
so that we have
![]() $z_{1}-\unicode[STIX]{x1D70F}_{d}^{\prime }\in (b_{1})$
. Hence
$z_{1}-\unicode[STIX]{x1D70F}_{d}^{\prime }\in (b_{1})$
. Hence
![]() $z_{1}\in QI^{2}+(b_{1})$
. The same argument works for each
$z_{1}\in QI^{2}+(b_{1})$
. The same argument works for each
![]() $1\leqslant i\leqslant d-1$
to see that
$1\leqslant i\leqslant d-1$
to see that
![]() $z_{i}\in QI^{2}+(b_{i})$
. Therefore, because
$z_{i}\in QI^{2}+(b_{i})$
. Therefore, because
![]() $I^{3}=QI^{2}+(z_{1},z_{2},\ldots ,z_{d-1})$
, we have
$I^{3}=QI^{2}+(z_{1},z_{2},\ldots ,z_{d-1})$
, we have
![]() $I^{3}\subseteq b_{d}I^{2}+(b_{1},b_{2},\ldots ,b_{d-1})$
and hence
$I^{3}\subseteq b_{d}I^{2}+(b_{1},b_{2},\ldots ,b_{d-1})$
and hence
Then, because
![]() $z_{d}+\unicode[STIX]{x1D70F}_{1}+b_{d}\unicode[STIX]{x1D70F}_{1}^{\prime }\in I^{4}$
, there exist elements
$z_{d}+\unicode[STIX]{x1D70F}_{1}+b_{d}\unicode[STIX]{x1D70F}_{1}^{\prime }\in I^{4}$
, there exist elements
![]() $h\in I^{2}$
and
$h\in I^{2}$
and
![]() $\unicode[STIX]{x1D702}\in (b_{1},b_{2},\ldots ,b_{d-1})$
such that
$\unicode[STIX]{x1D702}\in (b_{1},b_{2},\ldots ,b_{d-1})$
such that
![]() $z_{d}+\unicode[STIX]{x1D70F}_{1}+b_{d}\unicode[STIX]{x1D70F}_{1}^{\prime }=b_{d}^{2}h+\unicode[STIX]{x1D702}$
. Then we have
$z_{d}+\unicode[STIX]{x1D70F}_{1}+b_{d}\unicode[STIX]{x1D70F}_{1}^{\prime }=b_{d}^{2}h+\unicode[STIX]{x1D702}$
. Then we have
by the equality (2). Since
![]() $b_{1},b_{2},\ldots ,b_{d}$
is a regular sequence on
$b_{1},b_{2},\ldots ,b_{d}$
is a regular sequence on
![]() $A$
,
$A$
,
![]() $\unicode[STIX]{x1D702}\in (b_{d}^{2})\cap (b_{1},b_{2},\ldots ,b_{d-1})=b_{d}^{2}(b_{1},b_{2},\ldots ,b_{d-1})$
. Write
$\unicode[STIX]{x1D702}\in (b_{d}^{2})\cap (b_{1},b_{2},\ldots ,b_{d-1})=b_{d}^{2}(b_{1},b_{2},\ldots ,b_{d-1})$
. Write
![]() $\unicode[STIX]{x1D702}=b_{d}^{2}\unicode[STIX]{x1D702}^{\prime }$
with
$\unicode[STIX]{x1D702}=b_{d}^{2}\unicode[STIX]{x1D702}^{\prime }$
with
![]() $\unicode[STIX]{x1D702}^{\prime }\in (b_{1},b_{2},\ldots ,b_{d-1})$
, then we have
$\unicode[STIX]{x1D702}^{\prime }\in (b_{1},b_{2},\ldots ,b_{d-1})$
, then we have
by the equality (3), so that
![]() $z_{1}-\unicode[STIX]{x1D70F}_{d}^{\prime }-b_{1}h=b_{1}\unicode[STIX]{x1D702}^{\prime }$
. Then we have
$z_{1}-\unicode[STIX]{x1D70F}_{d}^{\prime }-b_{1}h=b_{1}\unicode[STIX]{x1D702}^{\prime }$
. Then we have
![]() $b_{1}\unicode[STIX]{x1D702}^{\prime }=z_{1}-\unicode[STIX]{x1D70F}_{d}^{\prime }-b_{1}h\in Q^{2}\cap I^{3}=Q^{2}I$
, since
$b_{1}\unicode[STIX]{x1D702}^{\prime }=z_{1}-\unicode[STIX]{x1D70F}_{d}^{\prime }-b_{1}h\in Q^{2}\cap I^{3}=Q^{2}I$
, since
![]() $Q^{2}\cap I^{3}\subseteq Q^{2}\cap \overline{Q^{3}}=Q^{2}\overline{Q}=Q^{2}I$
(cf. [Reference HunekeH, Reference ItohI2]), where
$Q^{2}\cap I^{3}\subseteq Q^{2}\cap \overline{Q^{3}}=Q^{2}\overline{Q}=Q^{2}I$
(cf. [Reference HunekeH, Reference ItohI2]), where
![]() $\overline{J}$
denotes the integral closure of an ideal
$\overline{J}$
denotes the integral closure of an ideal
![]() $J$
. Hence
$J$
. Hence
![]() $z_{1}\in QI^{2}$
, because
$z_{1}\in QI^{2}$
, because
![]() $\unicode[STIX]{x1D70F}_{d}^{\prime },b_{1}h,b_{1}\unicode[STIX]{x1D702}^{\prime }\in QI^{2}$
. Therefore,
$\unicode[STIX]{x1D70F}_{d}^{\prime },b_{1}h,b_{1}\unicode[STIX]{x1D702}^{\prime }\in QI^{2}$
. Therefore,
![]() $f_{1}=0$
in
$f_{1}=0$
in
![]() $C$
, which is impossible. Thus
$C$
, which is impossible. Thus
![]() $\ell =1$
so that we have
$\ell =1$
so that we have
![]() $\mathfrak{a}=(X_{1},X_{2},\ldots ,X_{d})B$
. Therefore,
$\mathfrak{a}=(X_{1},X_{2},\ldots ,X_{d})B$
. Therefore,
![]() $C=TC_{2}$
, that is
$C=TC_{2}$
, that is
![]() $I^{4}=QI^{3}$
. This completes the proof of Theorem 3.4 and that of Theorem 1.2 as well.◻
$I^{4}=QI^{3}$
. This completes the proof of Theorem 3.4 and that of Theorem 1.2 as well.◻
4 Consequences
The purpose of this section is to present some consequences of Theorem 1.2. Let us begin with the following which is exactly the case where
![]() $c=1$
in Theorem 1.2.
$c=1$
in Theorem 1.2.
Theorem 4.1. Assume that
![]() $I$
is integrally closed. Then the following conditions are equivalent.
$I$
is integrally closed. Then the following conditions are equivalent.
-
(1)
 $C\cong B(-2)$
as graded
$C\cong B(-2)$
as graded
 $T$
-modules.
$T$
-modules. -
(2)
 $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/IQ)+1$
, and if
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/IQ)+1$
, and if
 $d\geqslant 2$
then
$d\geqslant 2$
then
 $\text{e}_{2}(I)\neq \text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)$
.
$\text{e}_{2}(I)\neq \text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)$
. -
(3)
 $\ell _{A}(I^{3}/QI^{2})=1$
and
$\ell _{A}(I^{3}/QI^{2})=1$
and
 $I^{4}=QI^{3}$
.
$I^{4}=QI^{3}$
.
When this is the case, the following assertions follow.
-
(i)
 $\text{depth}G\geqslant d-1$
.
$\text{depth}G\geqslant d-1$
. -
(ii)
 $\text{e}_{2}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)+1$
if
$\text{e}_{2}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)+1$
if
 $d\geqslant 2$
.
$d\geqslant 2$
. -
(iii)
 $\text{e}_{3}(I)=1$
if
$\text{e}_{3}(I)=1$
if
 $d\geqslant 3$
, and
$d\geqslant 3$
, and
 $\text{e}_{i}(I)=0$
for
$\text{e}_{i}(I)=0$
for
 $4\leqslant i\leqslant d$
.
$4\leqslant i\leqslant d$
. -
(iv) The Hilbert series
 $HS_{I}(z)$
is given by
$HS_{I}(z)$
is given by  $$\begin{eqnarray}HS_{I}(z)=\frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-\ell _{A}(I^{2}/QI)\}z+\{\ell _{A}(I^{2}/QI)-1\}z^{2}+z^{3}}{(1-z)^{d}}.\end{eqnarray}$$
$$\begin{eqnarray}HS_{I}(z)=\frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-\ell _{A}(I^{2}/QI)\}z+\{\ell _{A}(I^{2}/QI)-1\}z^{2}+z^{3}}{(1-z)^{d}}.\end{eqnarray}$$
Proof. For
![]() $(1)\Leftrightarrow (2)$
,
$(1)\Leftrightarrow (2)$
,
![]() $(1)\Rightarrow (3)$
and the last assertions see Theorem 1.2 with
$(1)\Rightarrow (3)$
and the last assertions see Theorem 1.2 with
![]() $c=1$
.
$c=1$
.
![]() $(3)\Rightarrow (1)$
: Since
$(3)\Rightarrow (1)$
: Since
![]() $\mathfrak{m}I^{n+1}=Q^{n-1}I^{2}$
for all
$\mathfrak{m}I^{n+1}=Q^{n-1}I^{2}$
for all
![]() $n\geqslant 2$
, we have
$n\geqslant 2$
, we have
![]() $\mathfrak{m}C=(0)$
by Lemma 2.1(4). Then we have an epimorphism
$\mathfrak{m}C=(0)$
by Lemma 2.1(4). Then we have an epimorphism
![]() $B(-2)\rightarrow C\rightarrow 0$
of graded
$B(-2)\rightarrow C\rightarrow 0$
of graded
![]() $T$
-modules, which must be an isomorphism because
$T$
-modules, which must be an isomorphism because
![]() $\dim _{T}C=d$
(Proposition 2.2).◻
$\dim _{T}C=d$
(Proposition 2.2).◻
Let
![]() $\widetilde{J}=\bigcup _{n\geqslant 1}[J^{n+1}:_{A}J^{n}]=\bigcup _{n\geqslant 1}J^{n+1}:_{A}(a_{1}^{n},a_{2}^{n},\ldots ,a_{d}^{n})$
denote the Ratliff–Rush closure of an
$\widetilde{J}=\bigcup _{n\geqslant 1}[J^{n+1}:_{A}J^{n}]=\bigcup _{n\geqslant 1}J^{n+1}:_{A}(a_{1}^{n},a_{2}^{n},\ldots ,a_{d}^{n})$
denote the Ratliff–Rush closure of an
![]() $\mathfrak{m}$
-primary ideal
$\mathfrak{m}$
-primary ideal
![]() $J$
in
$J$
in
![]() $A$
, which is the largest
$A$
, which is the largest
![]() $\mathfrak{m}$
-primary ideal in
$\mathfrak{m}$
-primary ideal in
![]() $A$
such that
$A$
such that
![]() $J\subseteq \widetilde{J}$
and
$J\subseteq \widetilde{J}$
and
![]() $\text{e}_{i}(\widetilde{J})=\text{e}_{i}(J)$
for all
$\text{e}_{i}(\widetilde{J})=\text{e}_{i}(J)$
for all
![]() $0\leqslant i\leqslant d$
(cf. [Reference Ratliff and RushRR]).
$0\leqslant i\leqslant d$
(cf. [Reference Ratliff and RushRR]).
Let us note the following remark.
Remark 4.2. Assume that
![]() $I$
is integrally closed. Then, by [Reference HunekeH, Reference ItohI1],
$I$
is integrally closed. Then, by [Reference HunekeH, Reference ItohI1],
![]() $Q^{n}\cap \overline{I^{n+1}}=Q^{n}\cap \overline{Q^{n+1}}=Q^{n}\overline{Q}=Q^{n}I$
holds true for
$Q^{n}\cap \overline{I^{n+1}}=Q^{n}\cap \overline{Q^{n+1}}=Q^{n}\overline{Q}=Q^{n}I$
holds true for
![]() $n\geqslant 1$
, where
$n\geqslant 1$
, where
![]() $\overline{J}$
denotes the integral closure of an ideal
$\overline{J}$
denotes the integral closure of an ideal
![]() $J$
. Thus, we have
$J$
. Thus, we have
![]() $Q^{n}\cap \widetilde{I^{n+1}}=Q^{n}I$
for all
$Q^{n}\cap \widetilde{I^{n+1}}=Q^{n}I$
for all
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
The following result corresponds to the case where
![]() $c=d$
in Theorem 1.2. In Section 5 we give an example of the maximal ideal which satisfies assertion
$c=d$
in Theorem 1.2. In Section 5 we give an example of the maximal ideal which satisfies assertion
![]() $(1)$
in Theorem 4.3.
$(1)$
in Theorem 4.3.
Theorem 4.3. Suppose that
![]() $d\geqslant 2$
and assume that
$d\geqslant 2$
and assume that
![]() $I$
is integrally closed. Then the following conditions are equivalent:
$I$
is integrally closed. Then the following conditions are equivalent:
-
(1)
 $C\cong B_{+}(-1)$
as graded
$C\cong B_{+}(-1)$
as graded
 $T$
-modules.
$T$
-modules. -
(2)
 $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
,
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
,
 $\text{e}_{2}(I)=\ell _{A}(I^{2}/QI)+1$
, and
$\text{e}_{2}(I)=\ell _{A}(I^{2}/QI)+1$
, and
 $\text{e}_{i}(I)=0$
for all
$\text{e}_{i}(I)=0$
for all
 $3\leqslant i\leqslant d$
.
$3\leqslant i\leqslant d$
. -
(3)
 $\ell _{A}(\widetilde{I^{2}}/I^{2})=1$
and
$\ell _{A}(\widetilde{I^{2}}/I^{2})=1$
and
 $\widetilde{I^{n+1}}=Q\widetilde{I^{n}}$
for all
$\widetilde{I^{n+1}}=Q\widetilde{I^{n}}$
for all
 $n\geqslant 2$
.
$n\geqslant 2$
.
When this is the case, the associated graded ring
![]() $G$
of
$G$
of
![]() $I$
is a Buchsbaum ring with
$I$
is a Buchsbaum ring with
![]() $\text{depth}~G=0$
and the Buchsbaum invariant
$\text{depth}~G=0$
and the Buchsbaum invariant
![]() $\mathbb{I}(G)=d$
.
$\mathbb{I}(G)=d$
.
Proof. We set
![]() $c=\ell _{A}(I^{3}/QI^{2})$
and
$c=\ell _{A}(I^{3}/QI^{2})$
and
![]() ${\mathcal{F}}=\{\widetilde{I^{n}}\}_{n\geqslant 0}$
. Let
${\mathcal{F}}=\{\widetilde{I^{n}}\}_{n\geqslant 0}$
. Let
![]() $\text{R}^{\prime }({\mathcal{F}})=\sum _{n\in \mathbb{Z}}\widetilde{I^{n}}t\subseteq A[t,t^{-1}]$
and
$\text{R}^{\prime }({\mathcal{F}})=\sum _{n\in \mathbb{Z}}\widetilde{I^{n}}t\subseteq A[t,t^{-1}]$
and
![]() $\text{G}({\mathcal{F}})=\text{R}^{\prime }({\mathcal{F}})/t^{-1}\text{R}^{\prime }({\mathcal{F}})$
. Let
$\text{G}({\mathcal{F}})=\text{R}^{\prime }({\mathcal{F}})/t^{-1}\text{R}^{\prime }({\mathcal{F}})$
. Let
![]() $\text{e}_{i}({\mathcal{F}})$
denote the
$\text{e}_{i}({\mathcal{F}})$
denote the
![]() $i$
th Hilbert coefficients of the filtration
$i$
th Hilbert coefficients of the filtration
![]() ${\mathcal{F}}$
for
${\mathcal{F}}$
for
![]() $0\leqslant i\leqslant d$
.
$0\leqslant i\leqslant d$
.
![]() $(1)\Rightarrow (2)$
follows from Theorem 1.2, because
$(1)\Rightarrow (2)$
follows from Theorem 1.2, because
![]() $c=\ell _{A}(C_{2})=d$
.
$c=\ell _{A}(C_{2})=d$
.
![]() $(2)\Rightarrow (1)$
Because
$(2)\Rightarrow (1)$
Because
![]() $\text{e}_{2}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)$
and
$\text{e}_{2}(I)=\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)$
and
![]() $\text{e}_{i}(I)=0$
for all
$\text{e}_{i}(I)=0$
for all
![]() $3\leqslant i\leqslant d$
, we have
$3\leqslant i\leqslant d$
, we have
![]() $c=d$
by Theorem 1.2. Therefore
$c=d$
by Theorem 1.2. Therefore
![]() $C\cong B_{+}(-1)$
as graded
$C\cong B_{+}(-1)$
as graded
![]() $T$
-modules.
$T$
-modules.
![]() $(1)\Rightarrow (3)$
Since
$(1)\Rightarrow (3)$
Since
![]() $c=d$
, we have
$c=d$
, we have
![]() $\text{depth}G=0$
by Theorem 1.2
$\text{depth}G=0$
by Theorem 1.2
![]() $(ii)$
. We apply local cohomology functors
$(ii)$
. We apply local cohomology functors
![]() $\text{H}_{M}^{i}(\ast )$
of
$\text{H}_{M}^{i}(\ast )$
of
![]() $T$
with respect to the graded maximal ideal
$T$
with respect to the graded maximal ideal
![]() $M=\mathfrak{m}T+T_{+}$
of
$M=\mathfrak{m}T+T_{+}$
of
![]() $T$
to the exact sequences
$T$
to the exact sequences
of graded
![]() $T$
-modules and get derived monomorphisms
$T$
-modules and get derived monomorphisms
because
![]() $\text{depth}_{T}IR>0$
and
$\text{depth}_{T}IR>0$
and
![]() $\text{depth}_{T}I^{2}T\geqslant 2$
(recall that
$\text{depth}_{T}I^{2}T\geqslant 2$
(recall that
![]() $T$
is a Cohen–Macaulay ring with
$T$
is a Cohen–Macaulay ring with
![]() $\dim T=d+1$
and
$\dim T=d+1$
and
![]() $\text{depth}_{T}T/I^{2}T\geqslant 1$
by Lemma 2.3). We furthermore have
$\text{depth}_{T}T/I^{2}T\geqslant 1$
by Lemma 2.3). We furthermore have
![]() $\text{H}_{M}^{1}(C)\cong (B/B_{+})(-1)$
since
$\text{H}_{M}^{1}(C)\cong (B/B_{+})(-1)$
since
![]() $C\cong B_{+}(-1)$
. Since
$C\cong B_{+}(-1)$
. Since
![]() $I$
is integrally closed, we have
$I$
is integrally closed, we have
![]() $[\text{H}_{M}^{0}(G)]_{0}=(0)$
so that
$[\text{H}_{M}^{0}(G)]_{0}=(0)$
so that
![]() $\text{H}_{M}^{0}(G)\cong \text{H}_{M}^{0}(G_{+})\neq (0)$
. Then because
$\text{H}_{M}^{0}(G)\cong \text{H}_{M}^{0}(G_{+})\neq (0)$
. Then because
![]() $\ell _{A}(B/B_{+})=1$
, we have isomorphisms
$\ell _{A}(B/B_{+})=1$
, we have isomorphisms
of graded
![]() $B$
-modules and hence
$B$
-modules and hence
![]() $\text{H}_{M}^{0}(G)=[\text{H}_{M}^{0}(G)]_{1}\cong B/B_{+}$
. Then since
$\text{H}_{M}^{0}(G)=[\text{H}_{M}^{0}(G)]_{1}\cong B/B_{+}$
. Then since
![]() $[\text{H}_{M}^{0}(G)]_{1}\cong \widetilde{I^{2}}/I^{2}$
we have
$[\text{H}_{M}^{0}(G)]_{1}\cong \widetilde{I^{2}}/I^{2}$
we have
![]() $\ell _{A}(\widetilde{I^{2}}/I^{2})=1$
. Hence we have
$\ell _{A}(\widetilde{I^{2}}/I^{2})=1$
. Hence we have
 $$\begin{eqnarray}\displaystyle \text{e}_{1}({\mathcal{F}}) & = & \displaystyle \text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}({\mathcal{F}})-\ell _{A}(A/I)+\ell _{A}(\widetilde{I^{2}}/QI)+1-\ell _{A}(\widetilde{I^{2}}/I^{2})\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}({\mathcal{F}})-\ell _{A}(A/I)+\ell _{A}(\widetilde{I^{2}}/Q\cap \widetilde{I^{2}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{e}_{1}({\mathcal{F}}) & = & \displaystyle \text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}({\mathcal{F}})-\ell _{A}(A/I)+\ell _{A}(\widetilde{I^{2}}/QI)+1-\ell _{A}(\widetilde{I^{2}}/I^{2})\nonumber\\ \displaystyle & = & \displaystyle \text{e}_{0}({\mathcal{F}})-\ell _{A}(A/I)+\ell _{A}(\widetilde{I^{2}}/Q\cap \widetilde{I^{2}})\nonumber\end{eqnarray}$$
because
![]() $\widetilde{I}=I$
,
$\widetilde{I}=I$
,
![]() $Q\cap \widetilde{I^{2}}=QI$
by Remark 4.2, and
$Q\cap \widetilde{I^{2}}=QI$
by Remark 4.2, and
![]() $\text{e}_{i}({\mathcal{F}})=\text{e}_{i}(I)$
for
$\text{e}_{i}({\mathcal{F}})=\text{e}_{i}(I)$
for
![]() $i=0,1$
. Therefore,
$i=0,1$
. Therefore,
![]() $\widetilde{I^{n+1}}=Q\widetilde{I^{n}}$
for all
$\widetilde{I^{n+1}}=Q\widetilde{I^{n}}$
for all
![]() $n\geqslant 2$
by [Reference Guerrieri and RossiGR, Theorem 2.2].
$n\geqslant 2$
by [Reference Guerrieri and RossiGR, Theorem 2.2].
![]() $(3)\Rightarrow (2)$
Because
$(3)\Rightarrow (2)$
Because
![]() $Q\cap \widetilde{I^{2}}=QI$
by Remark 4.2 and
$Q\cap \widetilde{I^{2}}=QI$
by Remark 4.2 and
![]() $\widetilde{I^{n+1}}=Q\widetilde{I^{n}}$
for all
$\widetilde{I^{n+1}}=Q\widetilde{I^{n}}$
for all
![]() $n\geqslant 2$
, we have
$n\geqslant 2$
, we have
![]() $\text{e}_{1}({\mathcal{F}})=\text{e}_{0}({\mathcal{F}})-\ell _{A}(A/I)+\ell _{A}(\widetilde{I^{2}}/QI)$
and
$\text{e}_{1}({\mathcal{F}})=\text{e}_{0}({\mathcal{F}})-\ell _{A}(A/I)+\ell _{A}(\widetilde{I^{2}}/QI)$
and
![]() $\text{G}({\mathcal{F}})$
is a Cohen–Macaulay ring by [Reference Guerrieri and RossiGR, Theorem 2.2]. Then, since
$\text{G}({\mathcal{F}})$
is a Cohen–Macaulay ring by [Reference Guerrieri and RossiGR, Theorem 2.2]. Then, since
![]() $\ell _{A}(\widetilde{I^{2}}/I^{2})=1$
, we have
$\ell _{A}(\widetilde{I^{2}}/I^{2})=1$
, we have
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. We furthermore have
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. We furthermore have
![]() $\text{e}_{2}(I)=\text{e}_{2}({\mathcal{F}})=\ell _{A}(\widetilde{I^{2}}/QI)=\ell _{A}(I^{2}/QI)+1=\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)$
, and
$\text{e}_{2}(I)=\text{e}_{2}({\mathcal{F}})=\ell _{A}(\widetilde{I^{2}}/QI)=\ell _{A}(I^{2}/QI)+1=\text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)$
, and
![]() $\text{e}_{i}(I)=\text{e}_{i}({\mathcal{F}})=0$
for
$\text{e}_{i}(I)=\text{e}_{i}({\mathcal{F}})=0$
for
![]() $3\leqslant i\leqslant d$
, because
$3\leqslant i\leqslant d$
, because
![]() $\text{G}({\mathcal{F}})$
is a Cohen–Macaulay ring (cf. [Reference Huckaba and MarleyHM, Proposition 4.6]).
$\text{G}({\mathcal{F}})$
is a Cohen–Macaulay ring (cf. [Reference Huckaba and MarleyHM, Proposition 4.6]).
Assume one of the equivalent conditions. We have
![]() $\text{H}_{M}^{0}(G)=[\text{H}_{M}^{0}(G)]_{1}$
by the proof of the implication
$\text{H}_{M}^{0}(G)=[\text{H}_{M}^{0}(G)]_{1}$
by the proof of the implication
![]() $(1)\Rightarrow (3)$
. Let
$(1)\Rightarrow (3)$
. Let
![]() $n\geqslant 3$
be an integer. We then have
$n\geqslant 3$
be an integer. We then have
because
![]() $\widetilde{I^{n}}=Q^{n-2}\widetilde{I^{2}}\subseteq I^{n-1}$
. Therefore, we have
$\widetilde{I^{n}}=Q^{n-2}\widetilde{I^{2}}\subseteq I^{n-1}$
. Therefore, we have
![]() $\widetilde{I^{n}}=I^{n}$
for all
$\widetilde{I^{n}}=I^{n}$
for all
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
We set
![]() $W=\text{R}^{\prime }({\mathcal{F}})/R^{\prime }$
and look at the exact sequence
$W=\text{R}^{\prime }({\mathcal{F}})/R^{\prime }$
and look at the exact sequence
of graded
![]() $R^{\prime }$
-modules. Since
$R^{\prime }$
-modules. Since
![]() $\widetilde{I^{n}}=I^{n}$
for all
$\widetilde{I^{n}}=I^{n}$
for all
![]() $n\neq 2$
, we have
$n\neq 2$
, we have
![]() $W=W_{2}=\widetilde{I^{2}}/I^{2}$
so that
$W=W_{2}=\widetilde{I^{2}}/I^{2}$
so that
![]() $\ell _{A}(W)=1$
. Then, because
$\ell _{A}(W)=1$
. Then, because
![]() $\text{G}({\mathcal{F}})=\text{R}^{\prime }({\mathcal{F}})/t^{-1}\text{R}^{\prime }({\mathcal{F}})$
is a Cohen–Macaulay ring, so is
$\text{G}({\mathcal{F}})=\text{R}^{\prime }({\mathcal{F}})/t^{-1}\text{R}^{\prime }({\mathcal{F}})$
is a Cohen–Macaulay ring, so is
![]() $\text{R}^{\prime }({\mathcal{F}})$
. Let
$\text{R}^{\prime }({\mathcal{F}})$
. Let
![]() $M^{\prime }=(\mathfrak{m},R_{+},t^{-1})R^{\prime }$
be the unique graded maximal ideal in
$M^{\prime }=(\mathfrak{m},R_{+},t^{-1})R^{\prime }$
be the unique graded maximal ideal in
![]() $R^{\prime }$
. Then applying local cohomology functors
$R^{\prime }$
. Then applying local cohomology functors
![]() $\text{H}_{M^{\prime }}^{i}(\ast )$
to the exact sequence
$\text{H}_{M^{\prime }}^{i}(\ast )$
to the exact sequence
![]() $(\ast ^{\prime })$
yields
$(\ast ^{\prime })$
yields
![]() $\text{H}_{M^{\prime }}^{i}(R^{\prime })=(0)$
for all
$\text{H}_{M^{\prime }}^{i}(R^{\prime })=(0)$
for all
![]() $i\neq 1,d+1$
and
$i\neq 1,d+1$
and
![]() $\text{H}_{M^{\prime }}^{1}(R^{\prime })=W$
. Since
$\text{H}_{M^{\prime }}^{1}(R^{\prime })=W$
. Since
![]() $\mathfrak{m}W=(0)$
, we have
$\mathfrak{m}W=(0)$
, we have
![]() $\mathfrak{m}\text{H}_{M^{\prime }}^{1}(R^{\prime })=(0)$
. Thus,
$\mathfrak{m}\text{H}_{M^{\prime }}^{1}(R^{\prime })=(0)$
. Thus,
![]() $R^{\prime }$
is a Buchsbaum ring with the Buchsbaum invariant
$R^{\prime }$
is a Buchsbaum ring with the Buchsbaum invariant
and hence so is the graded ring
![]() $G=R^{\prime }/t^{-1}R^{\prime }$
. This completes the proof of Theorem 4.3.◻
$G=R^{\prime }/t^{-1}R^{\prime }$
. This completes the proof of Theorem 4.3.◻
In the rest of this section, we explore the relationship between the inequality of Northcott [Reference NorthcottN] and the structure of the graded module
![]() $C$
of an integrally closed ideal.
$C$
of an integrally closed ideal.
It is well known that the inequality
![]() $\text{e}_{1}(I)\geqslant \text{e}_{0}(I)-\ell _{A}(A/I)$
holds true [Reference NorthcottN] and the equality holds if and only if
$\text{e}_{1}(I)\geqslant \text{e}_{0}(I)-\ell _{A}(A/I)$
holds true [Reference NorthcottN] and the equality holds if and only if
![]() $I^{2}=QI$
[Reference HunekeH, Theorem 2.1]. When this is the case, the associated graded ring
$I^{2}=QI$
[Reference HunekeH, Theorem 2.1]. When this is the case, the associated graded ring
![]() $G$
of
$G$
of
![]() $I$
is Cohen–Macaulay.
$I$
is Cohen–Macaulay.
Suppose that
![]() $I$
is integrally closed and
$I$
is integrally closed and
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+1$
then, thanks to [Reference ItohI1, Corollary 14], we have
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+1$
then, thanks to [Reference ItohI1, Corollary 14], we have
![]() $I^{3}=QI^{2}$
and the associated graded ring
$I^{3}=QI^{2}$
and the associated graded ring
![]() $G$
of
$G$
of
![]() $I$
is Cohen–Macaulay. Thus the integrally closed ideal
$I$
is Cohen–Macaulay. Thus the integrally closed ideal
![]() $I$
with
$I$
with
![]() $\text{e}_{1}(I)\leqslant \text{e}_{0}(I)-\ell _{A}(A/I)+1$
seems understood in a satisfactory way. In this section, we briefly study the integrally closed ideals
$\text{e}_{1}(I)\leqslant \text{e}_{0}(I)-\ell _{A}(A/I)+1$
seems understood in a satisfactory way. In this section, we briefly study the integrally closed ideals
![]() $I$
with
$I$
with
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+2$
, and
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+2$
, and
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
.
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
.
Let us begin with the following.
Theorem 4.4. Assume that
![]() $I$
is integrally closed. Suppose that
$I$
is integrally closed. Suppose that
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+2$
and
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+2$
and
![]() $I^{3}\neq QI^{2}$
. Then the following assertions hold true.
$I^{3}\neq QI^{2}$
. Then the following assertions hold true.
-
(1)
 $\ell _{A}(I^{2}/QI)=\ell _{A}(I^{3}/QI^{2})=1$
, and
$\ell _{A}(I^{2}/QI)=\ell _{A}(I^{3}/QI^{2})=1$
, and
 $I^{4}=QI^{3}$
.
$I^{4}=QI^{3}$
. -
(2)
 $C\cong B(-2)$
as graded
$C\cong B(-2)$
as graded
 $T$
-modules.
$T$
-modules. -
(3)
 $\text{depth}~G=d-1$
.
$\text{depth}~G=d-1$
. -
(4)
 $\text{e}_{2}(I)=3$
if
$\text{e}_{2}(I)=3$
if
 $d\geqslant 2$
,
$d\geqslant 2$
,
 $\text{e}_{3}(I)=1$
if
$\text{e}_{3}(I)=1$
if
 $d\geqslant 3$
, and
$d\geqslant 3$
, and
 $\text{e}_{i}(I)=0$
for
$\text{e}_{i}(I)=0$
for
 $4\leqslant i\leqslant d$
.
$4\leqslant i\leqslant d$
. -
(5) The Hilbert series
 $HS_{I}(z)$
is given by
$HS_{I}(z)$
is given by  $$\begin{eqnarray}HS_{I}(z)=\frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-1\}z+z^{3}}{(1-z)^{d}}.\end{eqnarray}$$
$$\begin{eqnarray}HS_{I}(z)=\frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-1\}z+z^{3}}{(1-z)^{d}}.\end{eqnarray}$$
Proof. Because
![]() $I^{3}\neq QI^{2}$
, it follows from Corollary 2.10 that
$I^{3}\neq QI^{2}$
, it follows from Corollary 2.10 that
Thus,
![]() $\ell _{A}(I^{2}/QI)=1$
and
$\ell _{A}(I^{2}/QI)=1$
and
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. Let
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. Let
![]() $I^{2}=QI+(xy)$
with
$I^{2}=QI+(xy)$
with
![]() $x$
,
$x$
,
![]() $y\in I\backslash Q$
. Then
$y\in I\backslash Q$
. Then
![]() $I^{3}=QI^{2}+(x^{2}y)$
, so that
$I^{3}=QI^{2}+(x^{2}y)$
, so that
![]() $\ell _{A}(I^{3}/QI^{2})=1$
since
$\ell _{A}(I^{3}/QI^{2})=1$
since
![]() $I^{3}\neq QI^{2}$
and
$I^{3}\neq QI^{2}$
and
![]() $\mathfrak{m}I^{2}\subseteq QI$
. Thanks to Theorem 1.2,
$\mathfrak{m}I^{2}\subseteq QI$
. Thanks to Theorem 1.2,
![]() $C\cong B(-2)$
as graded
$C\cong B(-2)$
as graded
![]() $T$
-modules, so that assertions
$T$
-modules, so that assertions
![]() $(1)$
,
$(1)$
,
![]() $(2)$
,
$(2)$
,
![]() $(4)$
, and
$(4)$
, and
![]() $(5)$
follow, and
$(5)$
follow, and
![]() $\text{depth}~G\geqslant d-1$
by Theorem 4.1. Since
$\text{depth}~G\geqslant d-1$
by Theorem 4.1. Since
![]() $I^{3}\subseteq QI$
,
$I^{3}\subseteq QI$
,
![]() $G$
is not a Cohen–Macaulay ring, for otherwise
$G$
is not a Cohen–Macaulay ring, for otherwise
![]() $I^{3}=Q\cap I^{3}=QI^{2}$
, so that
$I^{3}=Q\cap I^{3}=QI^{2}$
, so that
![]() $\text{depth}G=d-1$
. This completes the proof of Theorem 4.4.◻
$\text{depth}G=d-1$
. This completes the proof of Theorem 4.4.◻
Notice that the following result also follows by [Reference Rossi and VallaRV3, Theorem 4.6].
Corollary 4.5. Assume that
![]() $I$
is integrally closed and suppose that
$I$
is integrally closed and suppose that
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+2$
. Then
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+2$
. Then
![]() $\text{depth}~G\geqslant d-1$
and
$\text{depth}~G\geqslant d-1$
and
![]() $I^{4}=QI^{3}$
, and the graded ring
$I^{4}=QI^{3}$
, and the graded ring
![]() $G$
is Cohen–Macaulay if and only if
$G$
is Cohen–Macaulay if and only if
![]() $I^{3}=QI^{2}$
.
$I^{3}=QI^{2}$
.
Before closing this section, we briefly study the integrally closed ideal
![]() $I$
with
$I$
with
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
. Suppose that
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
. Suppose that
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
then we have
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
then we have
by Corollary 2.10. If
![]() $\ell _{A}(I^{2}/QI)=1$
then we have
$\ell _{A}(I^{2}/QI)=1$
then we have
![]() $\text{depth}G\geqslant d-1$
by [Reference Rossi and VallaRV1, Reference WangW]. If
$\text{depth}G\geqslant d-1$
by [Reference Rossi and VallaRV1, Reference WangW]. If
![]() $\ell _{A}(I^{2}/QI)=3$
then the equality
$\ell _{A}(I^{2}/QI)=3$
then the equality
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
holds true, so that
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)$
holds true, so that
![]() $I^{3}=QI^{2}$
and the associated graded ring
$I^{3}=QI^{2}$
and the associated graded ring
![]() $G$
of
$G$
of
![]() $I$
is Cohen–Macaulay by Corollary 2.10. Thus we need to consider the following.
$I$
is Cohen–Macaulay by Corollary 2.10. Thus we need to consider the following.
Theorem 4.6. Suppose that
![]() $d\geqslant 2$
. Assume that
$d\geqslant 2$
. Assume that
![]() $I$
is integrally closed and
$I$
is integrally closed and
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
and
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
and
![]() $\ell _{A}(I^{2}/QI)=2$
. Let
$\ell _{A}(I^{2}/QI)=2$
. Let
![]() $c=\ell _{A}(I^{3}/QI^{2})$
. Then the following assertions hold true.
$c=\ell _{A}(I^{3}/QI^{2})$
. Then the following assertions hold true.
-
(1) Either
 $C\cong B(-2)$
as graded
$C\cong B(-2)$
as graded
 $T$
-modules or there exists an exact sequence of graded
$T$
-modules or there exists an exact sequence of graded $$\begin{eqnarray}0\rightarrow B(-3)\rightarrow B(-2)\oplus B(-2)\rightarrow C\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow B(-3)\rightarrow B(-2)\oplus B(-2)\rightarrow C\rightarrow 0\end{eqnarray}$$
 $T$
-modules.
$T$
-modules.
-
(2)
 $1\leqslant c\leqslant 2$
and
$1\leqslant c\leqslant 2$
and
 $I^{4}=QI^{3}$
.
$I^{4}=QI^{3}$
. -
(3) Suppose
 $c=1$
; then
$c=1$
; then
 $\text{depth}G\geqslant d-1$
and
$\text{depth}G\geqslant d-1$
and
 $\text{e}_{2}(I)=4$
,
$\text{e}_{2}(I)=4$
,
 $\text{e}_{3}(I)=1$
if
$\text{e}_{3}(I)=1$
if
 $d\geqslant 3$
, and
$d\geqslant 3$
, and
 $\text{e}_{i}(I)=0$
for
$\text{e}_{i}(I)=0$
for
 $4\leqslant i\leqslant d$
.
$4\leqslant i\leqslant d$
. -
(4) Suppose
 $c=2$
; then
$c=2$
; then
 $\text{depth}G=d-2$
and
$\text{depth}G=d-2$
and
 $\text{e}_{2}(I)=3$
,
$\text{e}_{2}(I)=3$
,
 $\text{e}_{3}(I)=-1$
if
$\text{e}_{3}(I)=-1$
if
 $d\geqslant 3$
,
$d\geqslant 3$
,
 $\text{e}_{4}(I)=-1$
if
$\text{e}_{4}(I)=-1$
if
 $d\geqslant 4$
, and
$d\geqslant 4$
, and
 $\text{e}_{i}(I)=0$
for
$\text{e}_{i}(I)=0$
for
 $5\leqslant i\leqslant d$
.
$5\leqslant i\leqslant d$
. -
(5) The Hilbert series
 $HS_{I}(z)$
is given by
$HS_{I}(z)$
is given by  $$\begin{eqnarray}HS_{I}(z)=\left\{\begin{array}{@{}rl@{}}\displaystyle \frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-2\}z+z^{2}+z^{3}}{(1-z)^{d}} & \quad \text{if }c=1,\\ \displaystyle \frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-2\}z+3z^{3}-z^{4}}{(1-z)^{d}} & \quad \text{if }c=2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}HS_{I}(z)=\left\{\begin{array}{@{}rl@{}}\displaystyle \frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-2\}z+z^{2}+z^{3}}{(1-z)^{d}} & \quad \text{if }c=1,\\ \displaystyle \frac{\ell _{A}(A/I)+\{\text{e}_{0}(I)-\ell _{A}(A/I)-2\}z+3z^{3}-z^{4}}{(1-z)^{d}} & \quad \text{if }c=2.\end{array}\right.\end{eqnarray}$$
Proof. Since
![]() $\ell _{A}(I^{2}/QI)=2$
and
$\ell _{A}(I^{2}/QI)=2$
and
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
, we have
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
, we have
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. We also have
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+\ell _{A}(I^{2}/QI)+1$
. We also have
![]() $1\leqslant \ell _{A}(I^{3}/QI^{2})\leqslant 2$
(see the proof of [Reference Rossi and VallaRV2, Propositions 2.1 and 2.2]). Then, thanks to Theorem 1.2,
$1\leqslant \ell _{A}(I^{3}/QI^{2})\leqslant 2$
(see the proof of [Reference Rossi and VallaRV2, Propositions 2.1 and 2.2]). Then, thanks to Theorem 1.2,
![]() $C\cong X_{1}B(-1)$
or
$C\cong X_{1}B(-1)$
or
![]() $C\cong (X_{1},X_{2})B(-1)$
as graded
$C\cong (X_{1},X_{2})B(-1)$
as graded
![]() $T$
-modules, where
$T$
-modules, where
![]() $X_{1}$
,
$X_{1}$
,
![]() $X_{2}$
denote the linearly independent linear forms of
$X_{2}$
denote the linearly independent linear forms of
![]() $B$
. Thus all assertions follow by Theorem 1.2.◻
$B$
. Thus all assertions follow by Theorem 1.2.◻
We remark that
![]() $\ell _{A}(I^{2}/QI)$
measures how far is the multiplicity of
$\ell _{A}(I^{2}/QI)$
measures how far is the multiplicity of
![]() $I$
from the minimal value (see [Reference Rossi and VallaRV3, Corollary 2.1]). If
$I$
from the minimal value (see [Reference Rossi and VallaRV3, Corollary 2.1]). If
![]() $\ell _{A}(I^{2}/QI)\leqslant 1,$
then
$\ell _{A}(I^{2}/QI)\leqslant 1,$
then
![]() $\text{depth}~G\geqslant d-1,$
but it is still open the problem whether
$\text{depth}~G\geqslant d-1,$
but it is still open the problem whether
![]() $\text{depth}G\geqslant d-2,$
assuming
$\text{depth}G\geqslant d-2,$
assuming
![]() $\ell _{A}(I^{2}/QI)=2$
. Theorem 4.6 confirms the conjectured bound.
$\ell _{A}(I^{2}/QI)=2$
. Theorem 4.6 confirms the conjectured bound.
Corollary 4.7. Assume that
![]() $I$
is integrally closed. Suppose that
$I$
is integrally closed. Suppose that
![]() $\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
. Then
$\text{e}_{1}(I)=\text{e}_{0}(I)-\ell _{A}(A/I)+3$
. Then
![]() $\text{depth}~G\geqslant d-2$
.
$\text{depth}~G\geqslant d-2$
.
Proof. We have
![]() $0<\ell _{A}(I^{2}/QI)\leqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)=3$
by Corollary 2.10. If
$0<\ell _{A}(I^{2}/QI)\leqslant \text{e}_{1}(I)-\text{e}_{0}(I)+\ell _{A}(A/I)=3$
by Corollary 2.10. If
![]() $\ell _{A}(I^{2}/QI)=1$
or
$\ell _{A}(I^{2}/QI)=1$
or
![]() $\ell _{A}(I^{2}/QI)=3$
then we have
$\ell _{A}(I^{2}/QI)=3$
then we have
![]() $\text{depth}G\geqslant d-1$
as above. Suppose that
$\text{depth}G\geqslant d-1$
as above. Suppose that
![]() $\ell _{A}(I^{2}/QI)=2$
then we have
$\ell _{A}(I^{2}/QI)=2$
then we have
![]() $\text{depth}G\geqslant d-2$
by Theorem 4.6(3), (4). This completes a proof of Corollary 4.7.◻
$\text{depth}G\geqslant d-2$
by Theorem 4.6(3), (4). This completes a proof of Corollary 4.7.◻
5 An example
The goal of this section is to construct an example of a Cohen–Macaulay local ring with the maximal ideal
![]() $\mathfrak{m}$
satisfying the equality in Theorem 1.2(1). The class of examples we exhibit includes an interesting example given by Wang, see [Reference Rossi and VallaRV3, Example 3.2].
$\mathfrak{m}$
satisfying the equality in Theorem 1.2(1). The class of examples we exhibit includes an interesting example given by Wang, see [Reference Rossi and VallaRV3, Example 3.2].
Theorem 5.1. Let
![]() $d\geqslant c\geqslant 1$
be integers. Then there exists a Cohen–Macaulay local ring
$d\geqslant c\geqslant 1$
be integers. Then there exists a Cohen–Macaulay local ring
![]() $(A,\mathfrak{m})$
such that
$(A,\mathfrak{m})$
such that
for some minimal reduction
![]() $Q=(a_{1},a_{2},\ldots ,a_{d})$
of
$Q=(a_{1},a_{2},\ldots ,a_{d})$
of
![]() $\mathfrak{m}$
.
$\mathfrak{m}$
.
To construct necessary examples we may assume that
![]() $c=d$
. In fact, suppose that
$c=d$
. In fact, suppose that
![]() $0<c<d$
and assume that we have already chosen a certain Cohen–Macaulay local ring
$0<c<d$
and assume that we have already chosen a certain Cohen–Macaulay local ring
![]() $(A_{0},\mathfrak{m}_{0})$
such that
$(A_{0},\mathfrak{m}_{0})$
such that
![]() $c=\operatorname{dim}A_{0}$
,
$c=\operatorname{dim}A_{0}$
,
![]() $\text{e}_{1}(\mathfrak{m}_{0})=\text{e}_{0}(\mathfrak{m}_{0})+\ell _{A_{0}}(\mathfrak{m}_{0}^{2}/Q_{0}\mathfrak{m}_{0})$
, and
$\text{e}_{1}(\mathfrak{m}_{0})=\text{e}_{0}(\mathfrak{m}_{0})+\ell _{A_{0}}(\mathfrak{m}_{0}^{2}/Q_{0}\mathfrak{m}_{0})$
, and
![]() $c=\ell _{A_{0}}(\mathfrak{m}_{0}^{3}/Q_{0}\mathfrak{m}_{0}^{2})$
with
$c=\ell _{A_{0}}(\mathfrak{m}_{0}^{3}/Q_{0}\mathfrak{m}_{0}^{2})$
with
![]() $Q_{0}=(a_{1},a_{2},\ldots ,a_{c})A_{0}$
a minimal reduction of
$Q_{0}=(a_{1},a_{2},\ldots ,a_{c})A_{0}$
a minimal reduction of
![]() $\mathfrak{m}_{0}$
. Let
$\mathfrak{m}_{0}$
. Let
![]() $n=d-c$
and let
$n=d-c$
and let
![]() $A=A_{0}[[X_{1},X_{2},\ldots ,X_{n}]]$
be the formal power series ring over the ring
$A=A_{0}[[X_{1},X_{2},\ldots ,X_{n}]]$
be the formal power series ring over the ring
![]() $A_{0}$
. We set
$A_{0}$
. We set
![]() $\mathfrak{m}=\mathfrak{m}_{0}A+(X_{1},X_{2},\ldots ,X_{n})A$
and
$\mathfrak{m}=\mathfrak{m}_{0}A+(X_{1},X_{2},\ldots ,X_{n})A$
and
![]() $Q=Q_{0}A+(X_{1},X_{2},\ldots ,X_{n})A$
. Then
$Q=Q_{0}A+(X_{1},X_{2},\ldots ,X_{n})A$
. Then
![]() $A$
is a Cohen–Macaulay local ring with
$A$
is a Cohen–Macaulay local ring with
![]() $\operatorname{dim}A=d$
and maximal ideal
$\operatorname{dim}A=d$
and maximal ideal
![]() $\mathfrak{m}=\mathfrak{m}_{0}A+(X_{1},X_{2},\ldots ,X_{n})A$
. The ideal
$\mathfrak{m}=\mathfrak{m}_{0}A+(X_{1},X_{2},\ldots ,X_{n})A$
. The ideal
![]() $Q$
is a reduction of
$Q$
is a reduction of
![]() $\mathfrak{m}$
and because
$\mathfrak{m}$
and because
![]() $X_{1},X_{2},\ldots ,X_{n}$
forms a super regular sequence in
$X_{1},X_{2},\ldots ,X_{n}$
forms a super regular sequence in
![]() $A$
with respect to
$A$
with respect to
![]() $\mathfrak{m}$
(recall that
$\mathfrak{m}$
(recall that
![]() $\text{G}(\mathfrak{m})=\text{G}(\mathfrak{m}_{0})[Y_{1},Y_{2},\ldots ,Y_{n}]$
is the polynomial ring, where
$\text{G}(\mathfrak{m})=\text{G}(\mathfrak{m}_{0})[Y_{1},Y_{2},\ldots ,Y_{n}]$
is the polynomial ring, where
![]() $Y_{i}$
’s are the initial forms of
$Y_{i}$
’s are the initial forms of
![]() $X_{i}$
’s), we have
$X_{i}$
’s), we have
![]() $\text{e}_{i}(\mathfrak{m})=\text{e}_{i}(\mathfrak{m}_{0})$
for
$\text{e}_{i}(\mathfrak{m})=\text{e}_{i}(\mathfrak{m}_{0})$
for
![]() $i=0,1$
,
$i=0,1$
,
![]() $\mathfrak{m}^{2}/Q\mathfrak{m}\cong \mathfrak{m}_{0}^{2}/Q_{0}\mathfrak{m}_{0}$
, and
$\mathfrak{m}^{2}/Q\mathfrak{m}\cong \mathfrak{m}_{0}^{2}/Q_{0}\mathfrak{m}_{0}$
, and
![]() $\mathfrak{m}^{3}/Q\mathfrak{m}^{2}\cong \mathfrak{m}_{0}^{3}/Q_{0}\mathfrak{m}_{0}^{2}$
. Thus we have
$\mathfrak{m}^{3}/Q\mathfrak{m}^{2}\cong \mathfrak{m}_{0}^{3}/Q_{0}\mathfrak{m}_{0}^{2}$
. Thus we have
![]() $\text{e}_{1}(\mathfrak{m})=\text{e}_{0}(\mathfrak{m})+\ell _{A}(\mathfrak{m}^{2}/Q\mathfrak{m})$
and
$\text{e}_{1}(\mathfrak{m})=\text{e}_{0}(\mathfrak{m})+\ell _{A}(\mathfrak{m}^{2}/Q\mathfrak{m})$
and
![]() $\ell _{A}(\mathfrak{m}^{3}/Q\mathfrak{m}^{2})=c$
. This observation allows us to concentrate our attention on the case where
$\ell _{A}(\mathfrak{m}^{3}/Q\mathfrak{m}^{2})=c$
. This observation allows us to concentrate our attention on the case where
![]() $c=d$
.
$c=d$
.
Let
![]() $m\geqslant 0$
and
$m\geqslant 0$
and
![]() $d\geqslant 1$
be integers. Let
$d\geqslant 1$
be integers. Let
be the formal power series ring with
![]() $m+2d+1$
indeterminates over an infinite field
$m+2d+1$
indeterminates over an infinite field
![]() $k$
, and let
$k$
, and let
We set
![]() $A=D/\mathfrak{a}$
and denote the images of
$A=D/\mathfrak{a}$
and denote the images of
![]() $X_{j}$
,
$X_{j}$
,
![]() $Y$
,
$Y$
,
![]() $V_{i}$
, and
$V_{i}$
, and
![]() $Z_{i}$
in
$Z_{i}$
in
![]() $A$
by
$A$
by
![]() $x_{j}$
,
$x_{j}$
,
![]() $y$
,
$y$
,
![]() $v_{i}$
, and
$v_{i}$
, and
![]() $a_{i}$
, respectively. Then, since
$a_{i}$
, respectively. Then, since
![]() $\sqrt{\mathfrak{a}}=(X_{j}|1\leqslant j\leqslant m)+(Y)+(V_{i}|1\leqslant i\leqslant d)$
, we have
$\sqrt{\mathfrak{a}}=(X_{j}|1\leqslant j\leqslant m)+(Y)+(V_{i}|1\leqslant i\leqslant d)$
, we have
![]() $\dim A=d$
. Let
$\dim A=d$
. Let
![]() $\mathfrak{m}=(x_{j}|1\leqslant j\leqslant m)+(y)+(v_{i}|1\leqslant i\leqslant d)+(a_{i}|1\leqslant i\leqslant d)$
be the maximal ideal in
$\mathfrak{m}=(x_{j}|1\leqslant j\leqslant m)+(y)+(v_{i}|1\leqslant i\leqslant d)+(a_{i}|1\leqslant i\leqslant d)$
be the maximal ideal in
![]() $A$
and we set
$A$
and we set
![]() $Q=(a_{i}|1\leqslant i\leqslant d)$
. Then,
$Q=(a_{i}|1\leqslant i\leqslant d)$
. Then,
![]() $\mathfrak{m}^{2}=Q\mathfrak{m}+(v_{i}^{2}|1\leqslant i\leqslant d)$
,
$\mathfrak{m}^{2}=Q\mathfrak{m}+(v_{i}^{2}|1\leqslant i\leqslant d)$
,
![]() $\mathfrak{m}^{3}=Q\mathfrak{m}^{2}+Qy$
, and
$\mathfrak{m}^{3}=Q\mathfrak{m}^{2}+Qy$
, and
![]() $\mathfrak{m}^{4}=Q\mathfrak{m}^{3}$
. Therefore
$\mathfrak{m}^{4}=Q\mathfrak{m}^{3}$
. Therefore
![]() $Q$
is a minimal reduction of
$Q$
is a minimal reduction of
![]() $\mathfrak{m}$
, and
$\mathfrak{m}$
, and
![]() $a_{1},a_{2},\ldots ,a_{d}$
is a system of parameters for
$a_{1},a_{2},\ldots ,a_{d}$
is a system of parameters for
![]() $A$
.
$A$
.
We are now interested in the Hilbert coefficients
![]() $\text{e}_{i}(\mathfrak{m})$
of the maximal ideal
$\text{e}_{i}(\mathfrak{m})$
of the maximal ideal
![]() $\mathfrak{m}$
as well as the structure of the associated graded ring
$\mathfrak{m}$
as well as the structure of the associated graded ring
![]() $\text{G}(\mathfrak{m})$
and the module
$\text{G}(\mathfrak{m})$
and the module
![]() $\text{C}_{Q}(\mathfrak{m})$
of
$\text{C}_{Q}(\mathfrak{m})$
of
![]() $\mathfrak{m}$
.
$\mathfrak{m}$
.
Theorem 5.2. The following assertions hold true.
-
(1)
 $A$
is a Cohen–Macaulay local ring with
$A$
is a Cohen–Macaulay local ring with
 $\dim A=d$
.
$\dim A=d$
. -
(2)
 $\text{C}_{Q}(\mathfrak{m})\cong B_{+}(-1)$
as graded
$\text{C}_{Q}(\mathfrak{m})\cong B_{+}(-1)$
as graded
 $T$
-modules. Therefore,
$T$
-modules. Therefore,
 $\ell _{A}(\mathfrak{m}^{3}/Q\mathfrak{m}^{2})=d$
.
$\ell _{A}(\mathfrak{m}^{3}/Q\mathfrak{m}^{2})=d$
. -
(3)
 $\text{e}_{0}(\mathfrak{m})=m+2d+2$
,
$\text{e}_{0}(\mathfrak{m})=m+2d+2$
,
 $\text{e}_{1}(\mathfrak{m})=m+3d+2$
.
$\text{e}_{1}(\mathfrak{m})=m+3d+2$
. -
(4)
 $\text{e}_{2}(\mathfrak{m})=d+1$
if
$\text{e}_{2}(\mathfrak{m})=d+1$
if
 $d\geqslant 2$
, and
$d\geqslant 2$
, and
 $\text{e}_{i}(\mathfrak{m})=0$
for all
$\text{e}_{i}(\mathfrak{m})=0$
for all
 $3\leqslant i\leqslant d$
.
$3\leqslant i\leqslant d$
. -
(5)
 $\text{G}(\mathfrak{m})$
is a Buchsbaum ring with
$\text{G}(\mathfrak{m})$
is a Buchsbaum ring with
 $\text{depth}\text{G}(\mathfrak{m})=0$
and
$\text{depth}\text{G}(\mathfrak{m})=0$
and
 $\mathbb{I}(\text{G}(\mathfrak{m}))=d$
.
$\mathbb{I}(\text{G}(\mathfrak{m}))=d$
. -
(6) The Hilbert series
 $HS_{\mathfrak{m}}(z)$
of
$HS_{\mathfrak{m}}(z)$
of
 $A$
is given by
$A$
is given by  $$\begin{eqnarray}HS_{\mathfrak{m}}(z)=\frac{1+\{m+d+1\}z+\mathop{\sum }_{j=3}^{d+2}(-1)^{j-1}\binom{d+1}{j-1}z^{j}}{(1-z)^{d}}.\end{eqnarray}$$
$$\begin{eqnarray}HS_{\mathfrak{m}}(z)=\frac{1+\{m+d+1\}z+\mathop{\sum }_{j=3}^{d+2}(-1)^{j-1}\binom{d+1}{j-1}z^{j}}{(1-z)^{d}}.\end{eqnarray}$$
Notice that Wang’s example before quoted corresponds to the particular case
![]() $m=0$
and
$m=0$
and
![]() $d=2.$
$d=2.$
Let us divide the proof of Theorem 5.2 into two steps. Let us begin with the following.
Proposition 5.3. Let
![]() $\mathfrak{p}=(X_{j}|1\leqslant j\leqslant m)+(Y)+(V_{i}|1\leqslant i\leqslant d)$
in
$\mathfrak{p}=(X_{j}|1\leqslant j\leqslant m)+(Y)+(V_{i}|1\leqslant i\leqslant d)$
in
![]() $D$
. Then
$D$
. Then
![]() $\ell _{D_{\mathfrak{p}}}(A_{\mathfrak{p}})=m+2d+2$
.
$\ell _{D_{\mathfrak{p}}}(A_{\mathfrak{p}})=m+2d+2$
.
Proof. Let
![]() $\widetilde{k}=k[\{Z_{i}\}_{1\leqslant i\leqslant d},\{\frac{1}{Z_{i}}\}_{1\leqslant i\leqslant d}]$
and
$\widetilde{k}=k[\{Z_{i}\}_{1\leqslant i\leqslant d},\{\frac{1}{Z_{i}}\}_{1\leqslant i\leqslant d}]$
and
![]() $\widetilde{D}=D[\{\frac{1}{Z_{i}}\}_{1\leqslant i\leqslant d}]$
. We set
$\widetilde{D}=D[\{\frac{1}{Z_{i}}\}_{1\leqslant i\leqslant d}]$
. We set
![]() $X_{j}^{\prime }=\frac{X_{j}}{Z_{1}}$
for
$X_{j}^{\prime }=\frac{X_{j}}{Z_{1}}$
for
![]() $1\leqslant j\leqslant m$
,
$1\leqslant j\leqslant m$
,
![]() $V_{i}^{\prime }=\frac{V_{i}}{Z_{1}}$
for
$V_{i}^{\prime }=\frac{V_{i}}{Z_{1}}$
for
![]() $1\leqslant i\leqslant d$
, and
$1\leqslant i\leqslant d$
, and
![]() $Y^{\prime }=\frac{Y}{Z_{1}}$
. Then we have
$Y^{\prime }=\frac{Y}{Z_{1}}$
. Then we have
 $$\begin{eqnarray}\displaystyle \widetilde{D} & = & \displaystyle \widetilde{k}[\{X_{j}^{\prime }|1\leqslant j\leqslant m\},Y^{\prime },\{V_{i}^{\prime }|1\leqslant i\leqslant d\}],\nonumber\\ \displaystyle \mathfrak{a}\widetilde{D} & = & \displaystyle [(X_{j}^{\prime }|1\leqslant j\leqslant m)+(Y^{\prime })]\cdot [(X_{j}^{\prime }|1\leqslant j\leqslant m)+(Y^{\prime })+(V_{i}^{\prime }|1\leqslant i\leqslant d)]\nonumber\\ \displaystyle & & \displaystyle +\,(V_{i}^{\prime }V_{j}^{\prime }|1\leqslant i,j\leqslant d,~i\neq j)+\biggl(\frac{Z_{1}^{2}}{Z_{i}}{V_{i}^{\prime }}^{3}-Y^{\prime }|1\leqslant i\leqslant d\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{D} & = & \displaystyle \widetilde{k}[\{X_{j}^{\prime }|1\leqslant j\leqslant m\},Y^{\prime },\{V_{i}^{\prime }|1\leqslant i\leqslant d\}],\nonumber\\ \displaystyle \mathfrak{a}\widetilde{D} & = & \displaystyle [(X_{j}^{\prime }|1\leqslant j\leqslant m)+(Y^{\prime })]\cdot [(X_{j}^{\prime }|1\leqslant j\leqslant m)+(Y^{\prime })+(V_{i}^{\prime }|1\leqslant i\leqslant d)]\nonumber\\ \displaystyle & & \displaystyle +\,(V_{i}^{\prime }V_{j}^{\prime }|1\leqslant i,j\leqslant d,~i\neq j)+\biggl(\frac{Z_{1}^{2}}{Z_{i}}{V_{i}^{\prime }}^{3}-Y^{\prime }|1\leqslant i\leqslant d\biggr),\nonumber\end{eqnarray}$$
and
![]() $\{X_{j}^{\prime }\}_{1\leqslant j\leqslant m}$
,
$\{X_{j}^{\prime }\}_{1\leqslant j\leqslant m}$
,
![]() $Y^{\prime }$
, and
$Y^{\prime }$
, and
![]() $\{V_{i}^{\prime }\}_{1\leqslant i\leqslant d}$
are algebraically independent over
$\{V_{i}^{\prime }\}_{1\leqslant i\leqslant d}$
are algebraically independent over
![]() $\widetilde{k}$
. Let
$\widetilde{k}$
. Let
in
![]() $\widetilde{D}$
and
$\widetilde{D}$
and
 $$\begin{eqnarray}\displaystyle \mathfrak{b} & = & \displaystyle [(X_{j}^{\prime }|1\leqslant j\leqslant m)+({V_{1}^{\prime }}^{3})]\cdot [(X_{j}^{\prime }|1\leqslant j\leqslant m)+(V_{i}^{\prime }|1\leqslant i\leqslant d)]\nonumber\\ \displaystyle & & \displaystyle +\,(V_{i}^{\prime }V_{j}^{\prime }|1\leqslant i,j\leqslant d,~i\neq j)+\biggl(\frac{Z_{1}^{2}}{Z_{i}}{V_{i}^{\prime }}^{3}-Z_{1}{V_{1}^{\prime }}^{3}|2\leqslant i\leqslant d\biggr)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{b} & = & \displaystyle [(X_{j}^{\prime }|1\leqslant j\leqslant m)+({V_{1}^{\prime }}^{3})]\cdot [(X_{j}^{\prime }|1\leqslant j\leqslant m)+(V_{i}^{\prime }|1\leqslant i\leqslant d)]\nonumber\\ \displaystyle & & \displaystyle +\,(V_{i}^{\prime }V_{j}^{\prime }|1\leqslant i,j\leqslant d,~i\neq j)+\biggl(\frac{Z_{1}^{2}}{Z_{i}}{V_{i}^{\prime }}^{3}-Z_{1}{V_{1}^{\prime }}^{3}|2\leqslant i\leqslant d\biggr)\nonumber\end{eqnarray}$$
in
![]() $W$
. Then substituting
$W$
. Then substituting
![]() $Y^{\prime }$
with
$Y^{\prime }$
with
![]() $Z_{1}{V_{1}^{\prime }}^{3}$
in
$Z_{1}{V_{1}^{\prime }}^{3}$
in
![]() $\widetilde{D}$
, we get the isomorphism
$\widetilde{D}$
, we get the isomorphism
of
![]() $\widetilde{k}$
algebras. Then the prime ideal
$\widetilde{k}$
algebras. Then the prime ideal
![]() $\mathfrak{p}\widetilde{D}/\mathfrak{a}\widetilde{D}$
corresponds to the prime ideal
$\mathfrak{p}\widetilde{D}/\mathfrak{a}\widetilde{D}$
corresponds to the prime ideal
![]() $P/\mathfrak{b}$
of
$P/\mathfrak{b}$
of
![]() $W/\mathfrak{b}$
, where
$W/\mathfrak{b}$
, where
![]() $P=W_{+}=(X_{j}^{\prime }|1\leqslant j\leqslant m)+(V_{i}^{\prime }|1\leqslant i\leqslant d)$
. Then because
$P=W_{+}=(X_{j}^{\prime }|1\leqslant j\leqslant m)+(V_{i}^{\prime }|1\leqslant i\leqslant d)$
. Then because
 $$\begin{eqnarray}\displaystyle \mathfrak{b}+({V_{1}^{\prime }}^{3}) & = & \displaystyle (X_{j}^{\prime }|1\leqslant j\leqslant m)\cdot [(X_{j}^{\prime }|1\leqslant j\leqslant m)+(V_{i}^{\prime }|1\leqslant i\leqslant d)]\nonumber\\ \displaystyle & & \displaystyle +\,(V_{i}^{\prime }V_{j}^{\prime }|1\leqslant i,j\leqslant d,~i\neq j)+({V_{i}^{\prime }}^{3}|1\leqslant i\leqslant d)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{b}+({V_{1}^{\prime }}^{3}) & = & \displaystyle (X_{j}^{\prime }|1\leqslant j\leqslant m)\cdot [(X_{j}^{\prime }|1\leqslant j\leqslant m)+(V_{i}^{\prime }|1\leqslant i\leqslant d)]\nonumber\\ \displaystyle & & \displaystyle +\,(V_{i}^{\prime }V_{j}^{\prime }|1\leqslant i,j\leqslant d,~i\neq j)+({V_{i}^{\prime }}^{3}|1\leqslant i\leqslant d)\nonumber\end{eqnarray}$$
and
![]() $\ell _{W_{P}}([\mathfrak{b}+({V_{1}^{\prime }}^{3})]W_{P}/\mathfrak{b}W_{P})=1$
, we get
$\ell _{W_{P}}([\mathfrak{b}+({V_{1}^{\prime }}^{3})]W_{P}/\mathfrak{b}W_{P})=1$
, we get
Thus
![]() $\ell _{A_{\mathfrak{p}}}(A_{\mathfrak{p}})=\ell _{W_{P}/\mathfrak{b}W_{P}}(W_{P}/\mathfrak{b}W_{P})=m+2d+2$
.◻
$\ell _{A_{\mathfrak{p}}}(A_{\mathfrak{p}})=\ell _{W_{P}/\mathfrak{b}W_{P}}(W_{P}/\mathfrak{b}W_{P})=m+2d+2$
.◻
Thanks to the associative formula of multiplicity, we have
because
![]() $\mathfrak{p}=\sqrt{\mathfrak{a}}$
and
$\mathfrak{p}=\sqrt{\mathfrak{a}}$
and
![]() $A/\mathfrak{p}A=D/\mathfrak{p}\cong k[[Z_{i}|1\leqslant i\leqslant d]]$
. On the other hand, we have
$A/\mathfrak{p}A=D/\mathfrak{p}\cong k[[Z_{i}|1\leqslant i\leqslant d]]$
. On the other hand, we have
where
Therefore,
![]() $\ell _{A}(A/Q)=m+2d+2$
. Thus
$\ell _{A}(A/Q)=m+2d+2$
. Thus
![]() $\text{e}_{0}(Q)=\ell _{A}(A/Q)$
so that
$\text{e}_{0}(Q)=\ell _{A}(A/Q)$
so that
![]() $A$
is a Cohen–Macaulay local ring with
$A$
is a Cohen–Macaulay local ring with
![]() $\text{e}_{0}(Q)=m+2d+2$
.
$\text{e}_{0}(Q)=m+2d+2$
.
Let
![]() $K_{0}=A$
,
$K_{0}=A$
,
![]() $K_{1}=\mathfrak{m}$
, and
$K_{1}=\mathfrak{m}$
, and
![]() $K_{n}=\mathfrak{m}^{n}+y\mathfrak{m}^{n-2}$
for
$K_{n}=\mathfrak{m}^{n}+y\mathfrak{m}^{n-2}$
for
![]() $n\geqslant 2$
, and we set
$n\geqslant 2$
, and we set
![]() ${\mathcal{K}}=\{K_{n}\}_{n\geqslant 0}$
. Let
${\mathcal{K}}=\{K_{n}\}_{n\geqslant 0}$
. Let
![]() $\text{e}_{i}({\mathcal{K}})$
denote the
$\text{e}_{i}({\mathcal{K}})$
denote the
![]() $i$
th Hilbert coefficients of the filtration
$i$
th Hilbert coefficients of the filtration
![]() ${\mathcal{K}}$
for
${\mathcal{K}}$
for
![]() $0\leqslant i\leqslant d$
.
$0\leqslant i\leqslant d$
.
Lemma 5.4. The following assertions hold true.
-
(1)
 $\ell _{A}(K_{2}/\mathfrak{m}^{2})=1$
and
$\ell _{A}(K_{2}/\mathfrak{m}^{2})=1$
and
 $K_{n}=\mathfrak{m}^{n}$
for all
$K_{n}=\mathfrak{m}^{n}$
for all
 $n\geqslant 3$
.
$n\geqslant 3$
. -
(2)
 $Q\cap K_{2}=QK_{1}$
and
$Q\cap K_{2}=QK_{1}$
and
 $K_{n+1}=QK_{n}$
for all
$K_{n+1}=QK_{n}$
for all
 $n\geqslant 2$
. Therefore,
$n\geqslant 2$
. Therefore,
 $\text{e}_{1}({\mathcal{K}})=\text{e}_{0}({\mathcal{K}})-\ell _{A}(A/K_{1})+\ell _{A}(K_{2}/QK_{1})$
,
$\text{e}_{1}({\mathcal{K}})=\text{e}_{0}({\mathcal{K}})-\ell _{A}(A/K_{1})+\ell _{A}(K_{2}/QK_{1})$
,
 $\text{e}_{2}({\mathcal{K}})=\ell _{A}(K_{2}/QK_{1})$
if
$\text{e}_{2}({\mathcal{K}})=\ell _{A}(K_{2}/QK_{1})$
if
 $d\geqslant 2$
, and
$d\geqslant 2$
, and
 $\text{e}_{i}({\mathcal{K}})=0$
for
$\text{e}_{i}({\mathcal{K}})=0$
for
 $3\leqslant i\leqslant d$
.
$3\leqslant i\leqslant d$
.
Proof. (1) Since
![]() $K_{2}=\mathfrak{m}^{2}+(y)$
, we have
$K_{2}=\mathfrak{m}^{2}+(y)$
, we have
![]() $\ell _{A}(K_{2}/\mathfrak{m}^{2})=1$
. We have
$\ell _{A}(K_{2}/\mathfrak{m}^{2})=1$
. We have
![]() $K_{n}=\mathfrak{m}^{n}+y\mathfrak{m}^{n-2}=\mathfrak{m}^{n}$
for all
$K_{n}=\mathfrak{m}^{n}+y\mathfrak{m}^{n-2}=\mathfrak{m}^{n}$
for all
![]() $n\geqslant 3$
, because
$n\geqslant 3$
, because
![]() $y\mathfrak{m}=(yv_{i}|1\leqslant i\leqslant d)=({v_{i}}^{3}|1\leqslant i\leqslant d)\subseteq \mathfrak{m}^{3}$
.
$y\mathfrak{m}=(yv_{i}|1\leqslant i\leqslant d)=({v_{i}}^{3}|1\leqslant i\leqslant d)\subseteq \mathfrak{m}^{3}$
.
![]() $(2)$
Since
$(2)$
Since
![]() $K_{n}=\mathfrak{m}^{n}$
for all
$K_{n}=\mathfrak{m}^{n}$
for all
![]() $n\geqslant 3$
by assertion
$n\geqslant 3$
by assertion
![]() $(1)$
, we have
$(1)$
, we have
![]() $K_{2}\subseteq \widetilde{\mathfrak{m}^{2}}$
. Therefore,
$K_{2}\subseteq \widetilde{\mathfrak{m}^{2}}$
. Therefore,
![]() $Q\cap K_{2}\subseteq Q\cap \widetilde{\mathfrak{m}^{2}}=Q\mathfrak{m}=QK_{1}$
by Remark 4.2. It is routine to check that
$Q\cap K_{2}\subseteq Q\cap \widetilde{\mathfrak{m}^{2}}=Q\mathfrak{m}=QK_{1}$
by Remark 4.2. It is routine to check that
![]() $K_{n+1}=QK_{n}$
for all
$K_{n+1}=QK_{n}$
for all
![]() $n\geqslant 2$
. Thus
$n\geqslant 2$
. Thus
![]() $\text{e}_{1}({\mathcal{K}})=\text{e}_{0}({\mathcal{K}})-\ell _{A}(A/K_{1})+\ell _{A}(K_{2}/QK_{1})$
by [Reference Guerrieri and RossiGR, Theorem 2.2]. We also have
$\text{e}_{1}({\mathcal{K}})=\text{e}_{0}({\mathcal{K}})-\ell _{A}(A/K_{1})+\ell _{A}(K_{2}/QK_{1})$
by [Reference Guerrieri and RossiGR, Theorem 2.2]. We also have
![]() $\text{e}_{2}({\mathcal{K}})=\ell _{A}(K_{2}/QK_{1})$
if
$\text{e}_{2}({\mathcal{K}})=\ell _{A}(K_{2}/QK_{1})$
if
![]() $d\geqslant 2$
, and
$d\geqslant 2$
, and
![]() $\text{e}_{i}({\mathcal{K}})=0$
for
$\text{e}_{i}({\mathcal{K}})=0$
for
![]() $3\leqslant i\leqslant d$
by [Reference Huckaba and MarleyHM, Proposition 4.6].◻
$3\leqslant i\leqslant d$
by [Reference Huckaba and MarleyHM, Proposition 4.6].◻
We prove now Theorem 5.2.
Proof of Theorem 5.2.
Since
![]() $K_{n}=\mathfrak{m}^{n}$
for all
$K_{n}=\mathfrak{m}^{n}$
for all
![]() $n\geqslant 3$
by Lemma 5.4(1), we have
$n\geqslant 3$
by Lemma 5.4(1), we have
![]() $\text{e}_{i}({\mathcal{K}})=\text{e}_{i}(\mathfrak{m})$
for
$\text{e}_{i}({\mathcal{K}})=\text{e}_{i}(\mathfrak{m})$
for
![]() $0\leqslant i\leqslant d$
. Therefore,
$0\leqslant i\leqslant d$
. Therefore,
![]() $\text{e}_{1}(\mathfrak{m})=\text{e}_{0}(\mathfrak{m})+\ell _{A}(\mathfrak{m}^{2}/Q\mathfrak{m})$
,
$\text{e}_{1}(\mathfrak{m})=\text{e}_{0}(\mathfrak{m})+\ell _{A}(\mathfrak{m}^{2}/Q\mathfrak{m})$
,
![]() $\text{e}_{2}(\mathfrak{m})=\ell _{A}(\mathfrak{m}^{2}/Q\mathfrak{m})+1$
if
$\text{e}_{2}(\mathfrak{m})=\ell _{A}(\mathfrak{m}^{2}/Q\mathfrak{m})+1$
if
![]() $d\geqslant 2$
, and
$d\geqslant 2$
, and
![]() $\text{e}_{i}(\mathfrak{m})=0$
for all
$\text{e}_{i}(\mathfrak{m})=0$
for all
![]() $3\leqslant i\leqslant d$
, because
$3\leqslant i\leqslant d$
, because
![]() $\ell _{A}(K_{2}/\mathfrak{m}^{2})=1$
,
$\ell _{A}(K_{2}/\mathfrak{m}^{2})=1$
,
![]() $\text{e}_{1}({\mathcal{K}})=\text{e}_{0}({\mathcal{K}})+\ell _{A}(K_{2}/QK_{1})-1$
,
$\text{e}_{1}({\mathcal{K}})=\text{e}_{0}({\mathcal{K}})+\ell _{A}(K_{2}/QK_{1})-1$
,
![]() $\text{e}_{2}({\mathcal{K}})=\ell _{A}(K_{2}/QK_{1})$
if
$\text{e}_{2}({\mathcal{K}})=\ell _{A}(K_{2}/QK_{1})$
if
![]() $d\geqslant 2$
, and
$d\geqslant 2$
, and
![]() $\text{e}_{i}({\mathcal{K}})=0$
for
$\text{e}_{i}({\mathcal{K}})=0$
for
![]() $3\leqslant i\leqslant d$
by Lemma 5.4. Then we have
$3\leqslant i\leqslant d$
by Lemma 5.4. Then we have
![]() $\text{e}_{1}(\mathfrak{m})=m+3d+2$
and
$\text{e}_{1}(\mathfrak{m})=m+3d+2$
and
![]() $\text{e}_{2}(\mathfrak{m})=d+1$
because
$\text{e}_{2}(\mathfrak{m})=d+1$
because
![]() $\text{e}_{0}(\mathfrak{m})=m+2d+2$
and
$\text{e}_{0}(\mathfrak{m})=m+2d+2$
and
![]() $\ell _{A}(\mathfrak{m}^{2}/Q\mathfrak{m})=d$
. The ring
$\ell _{A}(\mathfrak{m}^{2}/Q\mathfrak{m})=d$
. The ring
![]() $\text{G}(\mathfrak{m})$
is Buchsbaum ring with
$\text{G}(\mathfrak{m})$
is Buchsbaum ring with
![]() $\text{depth}\text{G}(\mathfrak{m})=0$
and
$\text{depth}\text{G}(\mathfrak{m})=0$
and
![]() $\mathbb{I}(\text{G}(\mathfrak{m}))=d$
by Theorem 4.3. This completes the proof of Theorem 5.2.◻
$\mathbb{I}(\text{G}(\mathfrak{m}))=d$
by Theorem 4.3. This completes the proof of Theorem 5.2.◻