Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T00:16:08.426Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure of the multiplicative group of residue classes modulo

Published online by Cambridge University Press:  22 January 2016

Norikata Nakagoshi
Norikata Nakagoshi*
Affiliation:
Department of Mathematics, College of Liberal Arts, Toyama University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

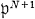
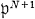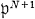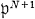Let k be an algebraic number field of finite degree and be a prime ideal of k, lying above a rational prime p. We denote by G () the multiplicative group of residue classes modulo (N ≧ 0) which are relatively prime to . The structure of G () is well-known, when N = 0, or k is the rational number field Q. If k is a quadratic number field, then the direct decomposition of G (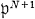) is determined by A. Ranum [6] and F.H-Koch [4] who gives a basis of a group of principal units in the local quadratic number field according to H. Hasse [2]. In [5, Theorem 6.2], W. Narkiewicz obtains necessary and sufficient conditions so that G (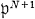) is cyclic, in connection with a group of units in the -adic completion of k.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 73 , March 1979 , pp. 41 - 60
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1979

References

[1] Albis Gonzalez, V. S., A remark on primitive root and ramification, Rev. Columbiana Math., 7 (1973), 93–98.Google Scholar
[2] Hasse, H., Zahlentheorie, Akademie-Verlag, Berlin, 2 Aufl., 1963.Google Scholar
[3] Hasse, H., Bericht über neuere Untersuchungen und Probleme aus der Theorie der algebraischen Zahlkörper, Physica Verlag, 1965.Google Scholar
[4] Koch, H.-F., Einseinheitengruppen und prime Restklassengruppen in quadratischen Zahlkörper, J. Number Theory, 4 (1972), 70–77.Google Scholar
[5] Narkiewicz, W., Elementary and analytic theory of algebraic numbers, Monogr. Math., 57, PWN-Polish Sci. Publishers, 1974.Google Scholar
[6] Ranum, A., The group of classes of congruent quadratic integers with respect to composite ideal modulus, Trans. Amer. Math. Soc., 11 (1910), 172–198.Google Scholar
[7] Serre, J.-P., Sur les corps locaux à corps résiduel algébriquement clos, Bull. Soc. Math. France, 89 (1961), 105–154.Google Scholar
[8] Takenouchi, T., On the classes of congruent integers in an algebraic körper, J. College of Sci. Tokyo Imp. Univ., XXXVI, Article I (1913), 1–28.Google Scholar
[9] Wyman, B. F., Wildly ramified Gamma extensions, Amer. J. Math., 91 (1969), 135–152.Google Scholar