Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1972.
Random Integral Equations.
Vol. 96,
Issue. ,
p.
218.
1972.
Random Integral Equations.
Vol. 96,
Issue. ,
p.
7.
Kuo, Hui-Hsiung
1973.
Stochastic Integrals in Abstruct Wiener Space II: Regularity Properties.
Nagoya Mathematical Journal,
Vol. 50,
Issue. ,
p.
89.
Dawson, D.A
1975.
Stochastic evolution equations and related measure processes.
Journal of Multivariate Analysis,
Vol. 5,
Issue. 1,
p.
1.
M�tivier, Michel
and
Pistone, Giovanni
1975.
Une formule d'isom�trie pour l'int�grale stochastique hilbertienne et �quations d'�volution lin�aires stochastiques.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 33,
Issue. 1,
p.
1.
Metivier, Michel
1975.
The Stochastic Integral with Respect to Processes with Values in a Reflexive Banach Space.
Theory of Probability & Its Applications,
Vol. 19,
Issue. 4,
p.
758.
Ichikawa, Akira
1978.
Linear stochastic evolution equations in Hilbert space.
Journal of Differential Equations,
Vol. 28,
Issue. 2,
p.
266.
1980.
Stochastic Integration.
p.
188.
Rascanu, A.
1981.
Existence for a class of stochastic parabolic variational inequalities.
Stochastics,
Vol. 5,
Issue. 3,
p.
201.
MITOMA, Itaru
1981.
MARTINGALES OF RANDOM DISTRIBUTIONS.
Memoirs of the Faculty of Science, Kyushu University. Series A, Mathematics,
Vol. 35,
Issue. 1,
p.
185.
Grecksch, W.
1981.
Eine ITO‐Formel für HILBERTraum‐wertige zufällige Felder.
Mathematische Nachrichten,
Vol. 101,
Issue. 1,
p.
179.
Krylov, N. V.
and
Rozovskii, B. L.
1981.
Stochastic evolution equations.
Journal of Soviet Mathematics,
Vol. 16,
Issue. 4,
p.
1233.
1982.
Semimartingales.
p.
273.
It�, Kiyosi
1983.
Distribution-valued processes arising from independent Brownian motions.
Mathematische Zeitschrift,
Vol. 182,
Issue. 1,
p.
17.
Loges, Wilfried
1984.
Girsanov's theorem in Hilbert space and an application to the statistics of Hilbert space- valued stochastic differential equations.
Stochastic Processes and their Applications,
Vol. 17,
Issue. 2,
p.
243.
P�rez-Abreu, V�ctor
1987.
Multiple wiener integrals and nonlinear functionals of a nuclear space valued Wiener process.
Applied Mathematics & Optimization,
Vol. 16,
Issue. 1,
p.
227.
Itô, Kiyosi
1987.
Selected Papers.
p.
629.
Mitoma, Itaru
1987.
Generalized ornstein-uhlenbeck process having a characteristic operator with polynomial coefficients.
Probability Theory and Related Fields,
Vol. 76,
Issue. 4,
p.
533.
Korezlioglu, Hayri
and
Martaias, Claude
1988.
Stochastic integration for operator valued processes on hilbert spaces and on nuclear spaces.
Stochastics,
Vol. 24,
Issue. 3,
p.
171.
Brooks, James K.
and
Neal, David
1989.
Seminar on Stochastic Processes, 1988.
p.
45.


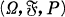 be a probability space and suppose we are given a family of σ-fields
be a probability space and suppose we are given a family of σ-fields 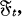
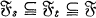 for O ≤
for O ≤ 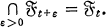 .
.