Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T23:32:52.019Z Has data issue: false hasContentIssue false
  • English
  • Français

Square of Brownian motion

Published online by Cambridge University Press:  22 January 2016

Hisao Nomoto
Hisao Nomoto*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Xt be a stochastic process and Yt be its square process. The present note is concerned with the solution of the equation 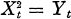assuming Yt is given. In [4], F. A. Grünbaum proved that certain statistics of Yt are enough to determine those of Xt when it is a centered, nonvanishing, Gaussian process with continuous correlation function. In connection with this result, we are interested in sample function-wise inference, though it is far from generalities. A glance of the equation 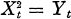shows that the difficulty is related how to pick up a sign of 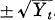. Thus if we know that Xt has nice sample process such as the zero crossings are finite, no tangencies, in any finite time interval, then observations of these statistics will make it sure to find out sample functions of Xt from those of Yt (see [2]). The purpose of this note is to consider the above problem from this point of view.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 59 , December 1975 , pp. 1 - 8
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1975

References

[1] Blumenthal, K. M. and Getoor, R. K., Markov processes and potential theory, Academic Press, New York, 1968.Google Scholar
[2] Cramer, H. and Leadbetter, R. M., Stationary and related stochastic processes, John Wiley and Sons., Inc., New York, 1967.Google Scholar
[3] Doob, J. L., Stochastic processes, John Wiley and Sons., Inc., New York, 1953.Google Scholar
[4] Grünbaum, F. A., The square of a Gaussian process, Z. Wahr. verw. Geb., 23, 121–124 (1972).CrossRefGoogle Scholar
[5] Mckean, H. P., Stochastic integrals, Academic Press, New York, 1969.Google Scholar
[6] Ito, K. and Mckean, H. P., Diffusion processes and their sample paths, Academic Press, New York, 1964.Google Scholar
[7] Skorohod, A., Stochastic equations for diffusion processes in a bounded region 1. 2, Th. Prob. its Appl. 6, 264–274 (1961); 7, 3–23 (1962).CrossRefGoogle Scholar