Article contents
Some Theorems on Open Riemann Surfaces
Published online by Cambridge University Press: 22 January 2016
Extract
Let F be an open Riemann surface spread over the z-plane. We say that F is of positive or null boundary, according as there exists a Green’s function on F or not, Let u(z) be a harmonic function on F
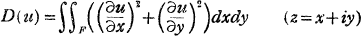
and be its Dirichlet integral As R. Nevanlinna proved, if F is of null boundary, there exists no one-valued non-constant harmonic function on F5 whose Dirichlet integral is finite, This Nevanlinna’s theorem was proved very simply by Kuroda.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1951
References
1) (a) R. Nevanlinna: Quadratisch integrierbare Differentiale auf einer Riemannschen Mannigfaltigkeit. Annales Acad. Sci, Fenn, Series A, Mathematica-Physica 1 (1941). (b) Über das Anwachsen des Dirichletintegrals- einer analytischen Funktion auf einer offenen Riemannschen Fläche. Annales Acad. Sci. Fenn. Series A, Mathematica-Physica 45 (1948)
2) T. Kuroda; Some remarks on an open Riemann surface. To appear in the Tohoku Math. Journ.
3) R. Nevanlinna. I.c. 1) (a).
4) R. Nevanlinna. I.c. 1) (a).
5) c. f. R. Nevanlinna. I.c. l) (a).
6) Heins, M.: The conformal mapping of simply connected Riemann surfaces. Annals of Math. 50 (1949).CrossRefGoogle Scholar
- 2
- Cited by


