No CrossRef data available.
Published online by Cambridge University Press: 17 February 2025
In this article, we discuss the topology of varieties over 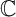 $\mathbb {C}$, viz., their homology and homotopy groups. We show that the fundamental group of a quasi-projective variety has negative deficiency under a certain hypothesis on its second homology and therefore a large class of groups cannot arise as fundamental groups of varieties. For a smooth projective surface admitting a fibration over a curve, we give a detailed analysis of the homology and homotopy groups of their universal cover via a case-by-case analysis, depending on the nature of the singular fibers. For smooth, projective surfaces whose universal cover is holomorphically convex (conjecturally always true), we show that the second and third homotopy groups are free abelian, often of infinite rank.
$\mathbb {C}$, viz., their homology and homotopy groups. We show that the fundamental group of a quasi-projective variety has negative deficiency under a certain hypothesis on its second homology and therefore a large class of groups cannot arise as fundamental groups of varieties. For a smooth projective surface admitting a fibration over a curve, we give a detailed analysis of the homology and homotopy groups of their universal cover via a case-by-case analysis, depending on the nature of the singular fibers. For smooth, projective surfaces whose universal cover is holomorphically convex (conjecturally always true), we show that the second and third homotopy groups are free abelian, often of infinite rank.