Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ohsawa, Takeo
2024.
Geometry of analytic continuation on complex manifolds – history, survey, and report.
Complex Manifolds,
Vol. 11,
Issue. 1,


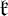 the real Lie algebra of a maximal compact real Lie subgroup
the real Lie algebra of a maximal compact real Lie subgroup 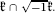 Then we obtain that there exists a plurisubharmonic, strongly (
Then we obtain that there exists a plurisubharmonic, strongly (