Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T23:42:05.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Some properties of ordinal diagrams

Published online by Cambridge University Press:  22 January 2016

Mariko Yasugi
Mariko Yasugi*
Affiliation:
Shizuoka University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theory of ordinal diagrams has been a most powerful means for consistency proofs of some systems of second order arithmetic. The last existing result in this line is the consistency proofs of the systems with the provably 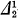-comprehension axiom and the 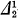-comprehension axiom respectively (cf. [6]). In order to pursue the consistency problem further, one needs investigate the theory of ordinal diagrams in two directions—refinement and strengthening of the theory.

For this purpose we have begun to search for some properties concerning ordinal diagrams and some variations of the theory of ordinal diagrams. The reader is requested to refer to §26 of [7] for the basic knowledge of ordinal diagrams.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 70 , July 1978 , pp. 143 - 155
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1978

References

[1] Takeuti, G., Ordinal diagrams, J. Math. Soc. Japan, 9 (1957), 386–394.Google Scholar
[2] Takeuti, G., Ordinal diagrams II, J. Math. Soc. Japan, 12 (1960), 385–391.Google Scholar
[3] Takeuti, G., Consistency proofs of subsystems of classical analysis, Annals of Mathematics 86 (1967), 299–348.Google Scholar
[4] Takeuti, G., The -comprehension schema and ω-rules, Proceedings of the Summer School in Logic (1967), Lecture Notes in Mathematics, 70 (1968), 303–330.Google Scholar
[5] Yasugi, M., Cut elimination theorem for second order arithmetic with the comprehension axiom and the ω-rule, J. Math. Soc. Japan, 22 (1970), 308–324.CrossRefGoogle Scholar
[6] Takeuti, G. and Yasugi, M., The ordinals of the systems of second order arithmetic with the provably -comprehension axiom and with the -comprehension axiom respectively, Japanese J. of Math., 41 (1973), 1–67.Google Scholar
[7] Takeuti, G., Proof Theory, North-Holland Publ. Co., Amsterdam, 1975.Google Scholar
[8] Takeuti, G. and Yasugi, M., Fundamental sequences of ordinal diagrams, Comentariorum Mathematicorum Universitatis Sancti Pauli, 25 (1976), 1–80.Google Scholar
[9] Takeuti, G. and Yasugi, M., An accessibility proof of ordinal diagrams, Mimeographed Notes.Google Scholar