Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jensen, Gary R.
1973.
Einstein metrics on principal fibre bundles.
Journal of Differential Geometry,
Vol. 8,
Issue. 4,
Sagle, Arthur A.
1974.
Jordan algebras and connections on homogeneous spaces.
Transactions of the American Mathematical Society,
Vol. 187,
Issue. 0,
p.
405.
Alekseevskii, D. V.
1975.
Lie groups and homogeneous spaces.
Journal of Soviet Mathematics,
Vol. 4,
Issue. 5,
p.
483.
Bourguignon, Jean Pierre
1981.
Global Differential Geometry and Global Analysis.
Vol. 838,
Issue. ,
p.
42.
Back, Allen
and
Hsiang, Wu-Yi
1987.
Equivariant geometry and Kervaire spheres.
Transactions of the American Mathematical Society,
Vol. 304,
Issue. 1,
p.
207.
Gavrilik, A. M.
1991.
Geometry in nonlinear quantumlike models on stiefel manifolds and bifurcations of associated autonomous systems.
Ukrainian Mathematical Journal,
Vol. 43,
Issue. 11,
p.
1418.
CHOQUET-BRUHAT, YVONNE
and
DEWITT-MORETTE, CÉCILE
2000.
Analysis, Manifolds and Physics.
p.
235.
Abbassi, Mohamed Tahar Kadaoui
and
Kowalski, Oldřich
2010.
On Einstein Riemannian g-natural metrics on unit tangent sphere bundles.
Annals of Global Analysis and Geometry,
Vol. 38,
Issue. 1,
p.
11.
Araújo, Fátima
2010.
Some Einstein homogeneous Riemannian fibrations.
Differential Geometry and its Applications,
Vol. 28,
Issue. 3,
p.
241.
Chen, Zhiqi
and
Liang, Ke
2014.
Non-naturally reductive Einstein metrics on the compact simple Lie group $$F_4$$ F 4.
Annals of Global Analysis and Geometry,
Vol. 46,
Issue. 2,
p.
103.
Arvanitoyeorgos, Andreas
Sakane, Yusuke
and
Statha, Marina
2014.
New homogeneous Einstein metrics on Stiefel manifolds.
Differential Geometry and its Applications,
Vol. 35,
Issue. ,
p.
2.
Tan, Ju
and
Xu, Na
2018.
Homogeneous Einstein–Randers metrics on some Stiefel manifolds.
Journal of Geometry and Physics,
Vol. 131,
Issue. ,
p.
182.
Tan, Ju
and
Xu, Na
2019.
Homogeneous Einstein–Randers metrics on symplectic groups.
Journal of Mathematical Analysis and Applications,
Vol. 472,
Issue. 2,
p.
1902.
Arvanitoyeorgos, Andreas
Sakane, Yusuke
and
Statha, Marina
2020.
Invariant Einstein metrics on $\mathrm{SU}(n)$ and complex Stiefel manifolds.
Tohoku Mathematical Journal,
Vol. 72,
Issue. 2,
Arvanitoyeorgos, Andreas
Sakane, Yusuke
and
Statha, Marina
2020.
Homogeneous Einstein metrics on Stiefel manifolds associated to flag manifolds with two isotropy summands.
Journal of Symbolic Computation,
Vol. 101,
Issue. ,
p.
189.
Chen, Huibin
Chen, Chao
and
Chen, Zhiqi
2021.
New Invariant Einstein–Randers Metrics on Stiefel Manifolds$$V_{2p}\mathbb {R}^n={\mathrm {S}}{\mathrm O}(n)/ {\mathrm {S}}{\mathrm O} (n-2p)$$.
Results in Mathematics,
Vol. 76,
Issue. 1,


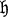 such that in the Lie algebra g of
such that in the Lie algebra g of 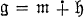 (subspace direct sum) and
(subspace direct sum) and 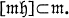 In this case the corresponding manifold
In this case the corresponding manifold 