Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T04:20:35.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Families of Componentwise Linear Monomial Ideals

Published online by Cambridge University Press:  11 January 2016

Christopher A. Francisco  and
Adam Van Tuyl
Christopher A. Francisco
Affiliation:
Department of Mathematics, Oklahoma State University, 401 Mathematical Sciences, Stillwater, OK [email protected], http://www.math.okstate.edu/~chris
Adam Van Tuyl
Affiliation:
Department of Mathematical Sciences, Lakehead University, Thunder Bay, ON P7B 5E1, Canada, [email protected], http://flash.lakeheadu.ca/~avantuyl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R = k[x1,…,xn] be a polynomial ring over a field k. Let J = {j1,…,jt} be a subset of {1,…, n}, and let mJ ⊂ R denote the ideal (xj1,…,xjt). Given subsets J1,…,Js of {1,…, n} and positive integers a1,…,as, we study ideals of the form 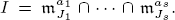These ideals arise naturally, for example, in the study of fat points, tetrahedral curves, and Alexander duality of squarefree monomial ideals. Our main focus is determining when ideals of this form are componentwise linear. Using polymatroidality, we prove that I is always componentwise linear when s ≤ 3 or when Ji ∪ Jj = [n] for all i ≠ j. When s ≥ 4, we give examples to show that I may or may not be componentwise linear. We apply these results to ideals of small sets of general fat points in multiprojective space, and we extend work of Fatabbi, Lorenzini, Valla, and the first author by computing the graded Betti numbers in the s = 2 case. Since componentwise linear ideals satisfy the Multiplicity Conjecture of Herzog, Huneke, and Srinivasan when char(k) = 0, our work also yields new cases in which this conjecture holds.

Keywords

13D4013D02
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 187 , September 2007 , pp. 115 - 156
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2007

References

[1] Aramova, A., Herzog, J. and Hibi, T., Ideals with stable Betti numbers, Adv. Math., 152 (2000), no. 1, 72–77.Google Scholar
[2] CoCoATeam, CoCoA: a system for doing Computations in Commutative Algebra, available at http://cocoa.dima.unige.it.Google Scholar
[3] Conca, A., Koszul homology and extremal properties of Gin and Lex, Trans. Amer. Math. Soc., 356 (2004), no. 7, 2945–2961.Google Scholar
[4] Conca, A. and Herzog, J., Castelnuovo-Mumford regularity of products of ideals, Collect. Math., 54 (2003), no. 2, 137–152.Google Scholar
[5] Eagon, J. and Northcott, D., Ideals defined by matrices and a certain complex, Proc. Roy. Soc. London A, 269 (1962), 188–204.Google Scholar
[6] Eagon, J. and Reiner, V., Resolutions of Stanley-Reisner rings and Alexander duality, J. Pure Appl. Algebra, 130 (1998), no. 3, 265–275.Google Scholar
[7] Eisenbud, D., Commutative algebra with a view toward algebraic geometry, Springer-Verlag, 1995.Google Scholar
[8] Eliahou, S. and Kervaire, M., Minimal resolutions of some monomial ideals, J. Algebra, 129 (1990), 1–25.CrossRefGoogle Scholar
[9] Faridi, S., Simplicial trees are sequentially Cohen-Macaulay, J. Pure Appl. Algebra, 190 (2003), 121–136.CrossRefGoogle Scholar
[10] Fatabbi, G., On the resolution of ideals of fat points, J. Algebra, 242 (2001), 92–108.Google Scholar
[11] Fatabbi, G. and Lorenzini, A., On the graded resolution of ideals of a few general fat points of Pn , J. Pure Appl. Algebra, 198 (2005), 123–150.CrossRefGoogle Scholar
[12] Francisco, C., Resolutions of small sets of fat points, J. Pure Appl. Algebra, 203 (2005), no. 1–3, 220–336.CrossRefGoogle Scholar
[13] Francisco, C., Migliore, J. and Nagel, U., On the componentwise linearity and the minimal free resolution of a tetrahedral curve, J. Algebra, 299 (2006), no. 2, 535–569.Google Scholar
[14] Francisco, C. and Tuyl, A. Van, Sequentially Cohen-Macaulay edge ideals, Proc. Amer. Math. Soc., 135 (2007), no. 8, 2327–2337.Google Scholar
[15] Gasharov, V., Hibi, T. and Peeva, I., Resolutions of a-stable ideals, J. Algebra, 254 (2002), no. 2, 375–394.Google Scholar
[16] Grayson, D. R. and Stillman, E. M., Macaulay 2, a software system for research in algebraic geometry, http://www.math.uiuc.edu/Macaulay2/.Google Scholar
[17] Guardo, E. and Tuyl, A. Van, Powers of complete intersections: graded Betti numbers and applications, Illinois J. Math., 49 (2005), no. 1, 265–279.CrossRefGoogle Scholar
[18] Herzog, J. and Hibi, T., Cohen-Macaulay polymatroidal ideals, European J. Combin., 27 (2006), no. 4, 513–517.CrossRefGoogle Scholar
[19] Herzog, J. and Hibi, T., Componentwise linear ideals, Nagoya Math. J., 153 (1999), 141–153.Google Scholar
[20] Herzog, J. and Hibi, T., Discrete polymatroids, J. Algebraic Combin., 16 (2002), no. 3, 239–268.Google Scholar
[21] Herzog, J., Reiner, V. and Welker, V., Componentwise linear ideals and Golod rings, Michigan Math. J., 46 (1999), no. 2, 211–223.Google Scholar
[22] Herzog, J. and Srinivasan, H., Bounds for multiplicities, Trans. Amer. Math. Soc., 350 (1998), no. 7, 2879–2902.Google Scholar
[23] Herzog, J. and Takayama, Y., Resolutions by mapping cones, The Roos Festschrift volume, 2, Homology Homotopy Appl., 4 (2002), no. 2, part 2, 277–294 (electronic).Google Scholar
[24] Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics 8, Cambridge University Press, Cambridge, 1989.Google Scholar
[25] Migliore, J. and Nagel, U., Tetrahedral curves, Int. Math. Res. Notices, 15 (2005), 899–939.Google Scholar
[26] Röomer, T., Note on bounds for multiplicities, J. Pure Appl. Algebra, 195 (2005), no. 1, 113–123.Google Scholar
[27] Stanley, R. P., Combinatorics and commutative algebra, Second edition, Progress in Mathematics 41, Birkhäuser Boston, Inc., Boston, MA, 1996.Google Scholar
[28] Valla, G., Betti numbers of some monomial ideals, Proc. Amer. Math. Soc., 133 (2005), 57–63.Google Scholar
[29] Tuyl, A. Van, The defining ideal of a set of points in multi-projective space, J. London Math. Soc., 72 (2005), 73–90.Google Scholar
[30] Tuyl, A. Van, The Hilbert functions of ACM sets of points in ℙn1 ·…× ℙnk , J. Algebra, 264 (2003), 420–441.Google Scholar
[31] Tuyl, A. Van, The border of the Hilbert function of a set of points in ℙn1 ·…× ℙnk , J. Pure Appl. Algebra, 176 (2002), 223–247.Google Scholar