Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DONG, Chen
and
MATSUZAWA, Tadato
1993.
<i>S</i>-spaces of Gel'fand-Shilov and differential equations.
Japanese journal of mathematics. New series,
Vol. 19,
Issue. 2,
p.
227.


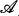
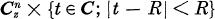 if 0 <
if 0 < 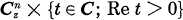 if
if 