Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Friedman, Avner
1979.
Stochastic Control Theory and Stochastic Differential Systems.
Vol. 16,
Issue. ,
p.
156.
Schuss, Zeev
1980.
Singular Perturbation Methods in Stochastic Differential Equations of Mathematical Physics.
SIAM Review,
Vol. 22,
Issue. 2,
p.
119.
Lavenda, B. H.
and
Santamato, E.
1982.
Thermodynamic criteria governing irreversible processes under the influence of small thermal fluctuations.
Journal of Statistical Physics,
Vol. 29,
Issue. 2,
p.
345.
Doss, Halim
and
Priouret, Pierre
1982.
Support d'un processus de r�flexion.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 61,
Issue. 3,
p.
327.
Doss, Halim
and
Priouret, Pierre
1983.
Séminaire de Probabilités XVII 1981/82.
Vol. 986,
Issue. ,
p.
353.
Lions, P. L.
and
Sznitman, A. S.
1984.
Stochastic differential equations with reflecting boundary conditions.
Communications on Pure and Applied Mathematics,
Vol. 37,
Issue. 4,
p.
511.
Lions, P.-L.
1985.
Neumann type boundary conditions for Hamilton-Jacobi equations.
Duke Mathematical Journal,
Vol. 52,
Issue. 4,
Jeulin, T.
1985.
Grossissements de filtrations: exemples et applications.
Vol. 1118,
Issue. ,
p.
197.
Frankowska, Halina
1985.
A viability approach to the skorohod problem.
Stochastics,
Vol. 14,
Issue. 3,
p.
227.
Varadhan, S. R. S.
and
Williams, R. J.
1985.
Brownian motion in a wedge with oblique reflection.
Communications on Pure and Applied Mathematics,
Vol. 38,
Issue. 4,
p.
405.
Dupuis, Paul
1987.
Large deviations analysis of reflected diffusions and constrained stochastic approximation algorithms in convex sets†.
Stochastics,
Vol. 21,
Issue. 1,
p.
63.
Perthame, Benoit
and
Sanders, Richard
1988.
The Neumann Problem for Nonlinear Second Order Singular Perturbation Problems.
SIAM Journal on Mathematical Analysis,
Vol. 19,
Issue. 2,
p.
295.
Safaryan, R G
1989.
BRANCHING DIFFUSION PROCESSES AND SYSTEMS OF REACTION-DIFFUSION DIFFERENTIAL EQUATIONS.
Mathematics of the USSR-Sbornik,
Vol. 62,
Issue. 2,
p.
525.
Graham, Carl
and
Métivier, Michel
1989.
System of interacting particles and nonlinear diffusion reflecting in a domain with sticky boundary.
Probability Theory and Related Fields,
Vol. 82,
Issue. 2,
p.
225.
Day, Martin V.
1989.
Boundary Local Time and Small Parameter Exit Problems with Characteristic Boundaries.
SIAM Journal on Mathematical Analysis,
Vol. 20,
Issue. 1,
p.
222.
Cranston, M.
and
Le Jan, Y.
1990.
Noncoalescence for the Skorohod equation in a convex domain of ℝ2
.
Probability Theory and Related Fields,
Vol. 87,
Issue. 2,
p.
241.
Day, Martin V.
1990.
Large deviations results for the exit problem with characteristic boundary.
Journal of Mathematical Analysis and Applications,
Vol. 147,
Issue. 1,
p.
134.
Axelrad, D. R.
1990.
Stochastic transport theory for porous media.
ZAMP Zeitschrift f�r angewandte Mathematik und Physik,
Vol. 41,
Issue. 2,
p.
157.
Barraquand, J.
and
Latombe, J.-C.
1990.
A Monte-Carlo algorithm for path planning with many degrees of freedom.
p.
1712.
Sudderth, W. D.
and
Weerasinghe, A. P. N.
1991.
Using fuel to control a process to a goal.
Stochastics and Stochastic Reports,
Vol. 34,
Issue. 3-4,
p.
169.


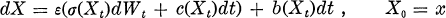 .
.