Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T23:02:05.068Z Has data issue: false hasContentIssue false
  • English
  • Français

A singular convolution kernel without pseudo-periods

Published online by Cambridge University Press:  22 January 2016

Jesper Laub
Jesper Laub*
Affiliation:
Matematisk Institut, Universitetsparken 5, DK-2100 København ø, Denmark
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a locally compact abelian group and N a non-zero convolution kernel on G satisfying the domination principle. We define the cone of N-excessive measures E(N) to be the set of positive measures ξ for which N satisfies the relative domination principle with respect to ξ. For ξ ∈ E(N) and Ω ⊆ G open the reduced measure of ξ over Ω is defined as

.

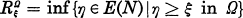Type
Research Article
Information
Nagoya Mathematical Journal , Volume 83 , October 1981 , pp. 1 - 4
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1981

References

[1] Berg, C. and Laub, J., The resolvent for a convolution kernel satisfying the domination principle, Preprint Series 1977 No. 41, Dept. of Math., Univ. of Copenhagen.Google Scholar
[2] Itô, M., Une caractérisation du principe de domination pour les noyaux de convolution, Japan J. Math., New series 1, No. 1 (1975), 5–35.Google Scholar
[3] Itô, M., Caractérisation du principe de domination pour les noyaux de convolution non-bornés, Nagoya Math., J., 57 (1975), 167–197.CrossRefGoogle Scholar
[4] Itô, M., Sur le principe relatif de domination pour les noyaux de convolution, Hiro shima Math. J., 5 (1975), 293–350.Google Scholar
[5] Laub, J., On unicity of the Riesz decomposition of an excessive measure, Math. Scand., to appear.Google Scholar