Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pernazza, L.
1995.
Decidability of the separation problem in dimension 2.
ANNALI DELL UNIVERSITA DI FERRARA,
Vol. 41,
Issue. 1,
p.
85.
Acquistapace, F.
Andradas, C.
and
Broglia, F.
1999.
Separation of semialgebraic sets.
Journal of the American Mathematical Society,
Vol. 12,
Issue. 3,
p.
703.


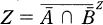 (where
(where 