Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T08:11:08.655Z Has data issue: false hasContentIssue false
  • English
  • Français

A Riesz decomposition theorem

Published online by Cambridge University Press:  22 January 2016

S. E. Graversen
S. E. Graversen*
Affiliation:
Department of Mathematics, Aarhus University, Ny Munkegade, 8000 Aarhus C, Denmark
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The topic of this note is the Riesz decomposition of excessive functions for a “nice” strong Markov process X. I.e. an excessive function is decomposed into a sum of a potential of a measure and a “harmonic” function. Originally such decompositions were studied by G.A. Hunt [8]. In [1] a Riesz decomposition is given assuming that the state space E is locally compact with a countable base and X is a transient standard process in strong duality with another standard process 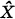having a strong Feller resolvent. Recently R.K. Getoor and J. Glover extended the theory to the case of transient Borei right processes in weak duality [6].

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 114 , June 1989 , pp. 123 - 133
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1989

References

[1] Blunienthal, R. M., Getoor, R. K., Markov processes and potential theory, New York, Academic Press, 1968.Google Scholar
[2] Chung, K. L., Rao, M., A new setting for potential theory, Ann. Inst. Fourier, 30 (1980), 167–198.Google Scholar
[3] Dellacherie, C., Capacités et processus stochastiques, Berlin-Heidelberg-New York, Springer Verlag, 1972.Google Scholar
[4] Dellacherie, C., Meyer, P. A., Probabilités et potentiel: Théorie discrète du potentiel, Herman, 1983.Google Scholar
[5] Getoor, R. K., Ray processes and right processes, Lecture Notes in Math., 440, Berlin-Heidelberg-New York, Springer Verlag, 1975.Google Scholar
[6] Getoor, R. K., Glover, J., Riesz decompositions in Markov process theory, Trans. Amer. Math. Soc, 285 (1984), 107–132.Google Scholar
[7] Getoor, R. K., Glover, J., Markov processes with identical excessive measures, Math. Z., 184 (1983), 187–300.Google Scholar
[8] Hunt, G. A., Markov processes and potentials I, Illinois J. Math., 1 (1957), 44–93.Google Scholar
[9] Liao, M., Riesz representation and duality of Markov processes, Séminaire de Probabilités XIX, 366–396, Lecture Notes in Math., 1123.Google Scholar
[10] Meyer, P. A., Probability and potentials, Blaisdell, 1966.Google Scholar
[11] Meyer, P. A., Processus de Markov: la frontière de Martin, Lecture Notes in Math., 77, Berlin-Heidelberg-New York, Springer Verlag, 1968.Google Scholar
[12] Mokobodzki, G., Densité relative de deux potentiels comparables, Lecture Notes in Math., 124, Sem. de Prob. IV (1970), 170–194.Google Scholar
[13] Mokobodzki, G., Dualité formelle et représentation des fonctions excessives, Actes du Congrès Int. des Mathématiciens, t. 2, 1970, 531–535.Google Scholar
[14] Walsh, J. B., The cofine topology revisited, Proc. Symp. in Pure Math., 31 (1977), 131–152. AMS, Providence.Google Scholar