It is well-known that the conformal equivalence of a compact simply-connected Riemann surface to the extended plane is readily established once it is shown that given a local uniformizer t(p) which carries a given point p0 of the surface into 0, there exists a function u harmonic on the surface save at p0 which admits near p0 a representation of the form

(α complex 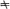0; h harmonic at p0). For the monodromy theorem then implies the existence of a meromorphic function on the surface whose real part is u. Such a meromorphic function has a simple pole at p0 and elsewhere is analytic. It defines a univalent conformal map of the surface onto the extended plane.