Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T23:16:41.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on extremal Kähler metrics on ruled manifolds

Published online by Cambridge University Press:  22 January 2016

Akira Fujiki
Akira Fujiki*
Affiliation:
Kyoto University and Yoshida College, Kyoto 606, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

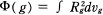Let X be a compact Kähler manifold and γ Kähler class. For a Kàhler metric g on X we denote by Rg the scalar curvature on X According to Calabi [3][4], consider the functional defined on the set of all the Kähler metrics g whose Kähler forms belong to γ, where dvg is the volume form associated to g. Such a Kähler metric is called extremal if it gives a critical point of Ф. In particular, if Rg is constant, g is extremal. The converse is also true if dim L(X) = 0, where L(X) is the maximal connected linear algebraic subgroup of AutoX (cf. [5]). Note also that any Kähler-Einstein metric is of constant scalar curvature.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 126 , June 1992 , pp. 89 - 101
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1992

References

[1] Burns, D. and de Baltolomeis, P., Stability of vector bundles and extremal metrics, Invent, math., 92 (1988), 403–408.CrossRefGoogle Scholar
[2] Bando, S. and Mabuchi, T., Uniqueness of Einstein-Kähler metrics modulo connected group actions, In: Oda, T. (ed.) Algebraic geometry, Proceeding, Sendai 1985 (Advanced Studies in Pure Math., 10, pp. 11–40): Kinokuniya and North-Holland 1986.Google Scholar
[3] Calabi, E., Extremal Kähler metrics, (Seminar on differential geometry, Yau, S.-T. ed., Princeton 1979), Ann, of Math. Studies, 102 (1982), 259–290.Google Scholar
[4] Calabi, E., Extremal Kähler metrics II, In: Differential geometry and complex analysis dedicated to Rauch, E. (Cheval, I. and Farkas, H. M.eds.) Springer-Verlag, 1985, 95–114.Google Scholar
[5] Fujiki, A., On automorphism groups of compact Kähler manifolds, Invent. Math., 44 (1978), 225–258.CrossRefGoogle Scholar
[6] Fujiki, A., On the uniqueness of generalized Kähler-Einstein metric, Math. Göttigenesis, Heft 46, 1988.Google Scholar
[7] Fujiki, A., Coarse moduli spaces for polarized compact Kähler manifolds, Publ. RIMS, Kyoto Univ., 20 (1984), 977–1005.CrossRefGoogle Scholar
[8] Fujiki, A. and Schumacher, G., On the moduli space of extremal compact Kähler manifolds, Publ. RIMS, Kyoto Univ., 26 (1990), 101–183.CrossRefGoogle Scholar
[9] Futaki, A., On compact Kähler manifolds of constant scalar curvature, Proc. Japan Acad., 59(1983), 401–402.Google Scholar
[10] Griffiths, P. A., Hermitian differential geometry, Chern classes, and positive vector bundles, In: Iyanaga, S., Spencer, D. C, (eds.) Global Analysis, Princeton Univ. Press, 1969.Google Scholar
[11] Harder, G., and Narasimhan, M. S., On the cohomology groups of the moduli spaces of vector bundles on curves, Math. Ann., 211 (1975), 215–248.CrossRefGoogle Scholar
[12] Hartshorne, R., “Algebraic geometry, Graduates Texts in Math., 52, Berlin-Heidelberg-New York: Springer, 1977.CrossRefGoogle Scholar
[13] Lange, H., Zur Klassifikation von Regelmannigfaltigkeiten, Math. Ann., 262 (1983), 447–459.CrossRefGoogle Scholar
[14] Levine, M., A remark extremal Kähler metrics, J. Diff. Geom, 21 (1985), 73–77.Google Scholar
[15] Lichnerowicz, A., Osométries et transformations analytiques d’;une variété kähérienne commpacte, Bull. Soc. Math. France, 87 (1959), 427–437.CrossRefGoogle Scholar
[16] Lichnerowicz, A., Variétés kählériennes à première classe de Chern non-négative et variétés riemanniennes à courbure de Ricci généralisée non-négative, J. Diff. Geom., 6(1971), 47–94.Google Scholar
[17] Maruyama, M., On automorphism groups of ruled surfaces, J. Math. Kyoto Univ., 11 (1971), 89–112.Google Scholar
[18] Narasimhan, M. S., and Seshadri, C. S., Stable and unitary vector bundles on a compact Riemann surface, Ann. of Math., 82 (1965), 540–567.CrossRefGoogle Scholar
[19] Ramanathan, A., Stable principal bundles on a compact Riemann surface, Math. Ann., 213(1975), 129–152.CrossRefGoogle Scholar
[20] Suwa, T., Ruled surfaces of genus one, J. Math. Soc. Japan, 2 (1969), 258–291.Google Scholar
[21] Yau, S. T. On the curvature of compact Hermitian manifolds, Invent. Math, 25 (1974), 213–239.CrossRefGoogle Scholar